cerchio

Astronomia

fig. 1

C. di altezza

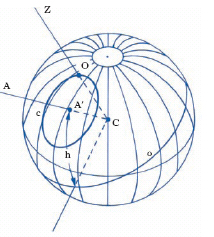
In astronomia nautica, circonferenza (c in fig. 1) tracciata sulla sfera terrestre, avente per centro la proiezione su quest’ultima, dal suo centro, di un astro A, e per raggio sferico il complemento dell’altezza h di A misurata da un osservatore in un certo istante. È il luogo delle posizioni di tutti gli osservatori che nel medesimo istante misurano la stessa altezza di quell’astro, onde la posizione dell’osservatore (punto-nave) è data da una delle due intersezioni di due c. di altezza relativa allo stesso istante e corrispondenti a due distinti astri.

C. azimutale

In strumenti astronomici e topografici, cerchio graduato per la misurazione di angoli azimutali.

C. graduato

In vari strumenti, in particolare astronomici e topografici, corona circolare o disco metallico o di vetro, su cui sono incise le graduazioni angolari dell’angolo giro variamente suddivise e numerate.

C. orario di un astro

C. massimo della sfera celeste passante per i poli celesti e per un dato astro.

Per il c. meridiano

➔ meridiano.

Matematica

In geometria, la superficie piana racchiusa da una circonferenza, definita come il luogo dei punti del piano aventi da un punto C (centro) distanza minore o uguale di un assegnato valore r (raggio del c. o della circonferenza).

Definizioni

fig. 2

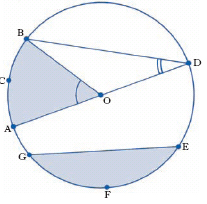
Nel c. segmenti come OA, OB in fig. 2, che congiungono il centro con un punto della circonferenza, si dicono  raggi; ogni retta passante per il c. (e anche il segmento di questa intercettato dalla circonferenza, come AD), si dice diametro.

Corda è un segmento con entrambi gli estremi sulla circonferenza (come BD, EG); le corde di lunghezza massima sono i diametri. Arco è una parte qualunque della circonferenza (come ACBD, EFG); la corda congiungente gli estremi di un arco si dice che sottende l’arco stesso.

Angolo al centro è un angolo avente il vertice nel centro del c. (A∧OB).

Angolo alla circonferenza (A∧DB) è un angolo, avente il vertice sulla circonferenza, che tra i suoi lati intercetta un arco di circonferenza (come caso limite un lato dell’angolo alla circonferenza può essere tangente alla circonferenza stessa, nel suo vertice).

Segmento circolare (GEF) è la parte di c. limitata da un suo arco e dalla corda che lo sottende; ogni corda divide il c. in due segmenti circolari situati da bande opposte rispetto a essa.

Settore circolare (OBCA) è la parte di c. limitata da un arco e dai due raggi passanti per gli estremi di questo. Un punto si dice esterno o interno al c., secondo che la sua distanza dal centro sia maggiore o minore del raggio. Una retta si dice esterna, tangente o secante rispetto a un c., più propriamente rispetto alla circonferenza contorno, secondo che abbia nessun punto, un punto, due punti comuni con la circonferenza; ciascuno dei tre casi si presenta, nell’ordine, secondo che la distanza della retta dal centro sia maggiore, uguale, minore del raggio. Due c. di raggio r e r′, (più propriamente le rispettive circonferenze) i cui centri siano a distanza d, sono: esterni se d>r+r′; tangenti esternamente se d=r+r′; secanti se r–r′⟨d⟨r+r′ (supposto r>r′); tangenti internamente se d=r–r′; interni (il minore nel maggiore) se d⟨r–r′).

Proprietà

L’antichità classica considerò il c. figura ‘perfetta’ per la sua facile costruibilità con l’uso del compasso e soprattutto per la sua simmetria; al c. si riferisce gran parte dei problemi della geometria classica. Quasi tutte le sue proprietà elementari si trovano esposte nel libro III degli Elementi di Euclide.

Proprietà delle corde

Corde uguali sottendono archi uguali; ogni corda è dimezzata dal diametro a essa perpendicolare (teorema invertibile); due corde che si taglino (internamente o esternamente al c.) si dividono in parti inversamente proporzionali. Di qui si deduce che il prodotto delle distanze di un punto P dagli estremi di una corda condotta per esso non dipende dalla corda considerata: tale prodotto si chiama potenza di P rispetto al c. (o alla circonferenza contorno).

Proprietà delle tangenti

Una tangente è perpendicolare al raggio passante per il punto di contatto; da un punto esterno si possono condurre due tangenti al c.; condotta una tangente da un punto P esterno a un c., il quadrato del segmento compreso fra P e il punto di contatto è uguale alla potenza di P rispetto al cerchio.

Proprietà degli angoli alla circonferenza

Tutti gli angoli alla circonferenza che insistono sullo stesso arco sono uguali tra loro, e uguali alla metà dell’angolo al centro i cui lati vanno all’estremo dell’arco (in fig. 2, A∧DB=A∧OB/2): reciprocamente, il luogo dei punti del piano da cui un dato segmento è visto sotto un angolo costante è un arco di circonferenza che ha quel segmento come corda; in particolare l’angolo che insiste su una semicirconferenza è retto.

Misure relative al cerchio

Area del c. (di raggio r): π r² (per il numero π ➔ pi). Area del settore circolare (ϑ è la misura, in radianti, dell’angolo al centro relativo all’arco): r² ϑ/2.

Area del segmento circolare: r² (ϑ−sen ϑ)/2.

Quadratura del cerchio

Non è possibile per via elementare (servendosi solo della riga e del compasso) eseguire la quadratura del c., ossia costruire un quadrato avente area uguale all’area del c. dato. Poiché l’area del c. di raggio r è S=π r², il lato del quadrato cercato dovrebbe avere lunghezza l=r √‾‾π. La suddetta impossibilità (dimostrata da F. Lindemann nel 1882) è dovuta al fatto che π è un numero irrazionale trascendente (non è radice di alcuna equazione algebrica a coefficienti interi). L’impossibilità di quadrare il c. per via elementare non vuol dire, come talora erroneamente si crede, che non esista un quadrato equivalente a un c. dato; tale quadrato esiste, e il suo lato, come si è visto, vale r √‾‾π: ciò che è impossibile è costruire tale quadrato, a partire dal cerchio dato, servendosi solo degli strumenti elementari. Ma fin dall’antichità si sapeva risolvere il problema con l’impiego di mezzi superiori (curve diverse dalla retta e dal c.; ➔ quadratrice).

Medicina

In patologia, c. corneo (o di Kayser-Fleischer), anello di pigmentazione bruno-verdastra, interessante la parte periferica della cornea, che compare in caso di degenerazione epato-lenticolare.