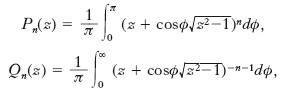sfera

sfera In geometria, figura solida formata dai punti dello spazio aventi da un punto fissato (centro della s.) distanza minore o uguale di un segmento dato (raggio della s.).

Matematica

Definizioni e proprietà principali

Molte nozioni e proprietà riguardanti la s. si possono considerare come un’estensione di concetti analoghi relativi al cerchio. Si chiama corda un segmento avente gli estremi sulla superficie sferica; i diametri (uguali tutti al doppio del raggio e passanti per il centro) sono le corde di lunghezza massima. Antipodi o punti antipodali o punti diametralmente opposti sono gli estremi di uno stesso diametro.

Una retta è esterna, tangente, secante una s. a seconda che la sua distanza dal centro della s. sia maggiore, uguale, minore del raggio. Lo stesso può dirsi a proposito dei piani. Per una retta esterna passano due piani tangenti che separano i piani secanti da quelli esterni, per una retta tangente c’è un solo piano tangente e infiniti piani secanti, per una retta secante passano solo piani secanti; viceversa, su un piano secante esistono rette dei tre tipi, su un piano tangente solo rette tangenti ed esterne, e infine su un piano esterno unicamente rette esterne. Sia una retta tangente sia un piano tangente sono perpendicolari al diametro che passa per il punto di contatto.

Tutte le sezioni piane di una s. sono cerchi. Se un piano secante passa per il centro (piano meridiano), la sua sezione con la s. è un cerchio (o circolo) massimo, ossia un cerchio di raggio uguale al raggio della s., più grande di tutti gli altri cerchi della s.; in caso contrario è un cerchio minore, il cui raggio è tanto più piccolo quanto più il piano è prossimo a essere un piano tangente; per ragioni di continuità, nel caso di un piano tangente a una s. il punto di contatto si può considerare come un cerchio di raggio nullo.

Si chiamano poli di un cerchio sezione di una s. gli estremi del diametro della s. che è perpendicolare al piano del cerchio. Due s. di raggi R, R′ i cui centri siano a distanza d sono: a) esterne se d>R+R′; b) tangenti esternamente se d=R+R′; c) secanti se R−R′<d<R+R′ (supposto R>R′); d) tangenti internamente se d=R−R′; e) una interna all’altra se d<R−R′.

Misure relative alla sfera

La superficie della s. di raggio R vale 4πR² e risulta quindi pari all’area di quattro cerchi massimi. Il volume della s. è dato da (4/3)πR³ ed è uguale al quadruplo del volume del cono circolare retto che ha per base un cerchio massimo e per altezza il raggio. La determinazione del volume e dell’area della s. è una delle grandi scoperte di Archimede.

Parti della s. e della superficie sferica

Calotta sferica Una delle due parti nelle quali la superficie sferica è suddivisa da un piano secante; vertice della calotta è il punto che ha la massima distanza (detta altezza) da tale piano. La superficie di una calotta di altezza h e appartenente a una s. di raggio R è data da 2πRh. Fuso sferico La parte di superficie sferica compresa tra due semipiani uscenti da un medesimo diametro. Indicato con R il raggio della s. e con α l’angolo (in gradi) formato da due semipiani, l’area del fuso è data da πR²α/90. Poligono sferico Una parte di superficie sferica delimitata da archi di cerchi massimi. Segmento sferico a una base La parte di s. delimitata da un piano secante. Il volume è dato da V=πh(3a²+h²)/6 ove h è l’altezza del segmento e a il raggio del cerchio base. Segmento sferico a due basi La parte di s. compresa tra due piani secanti paralleli; indicando con h la loro distanza (altezza del segmento) e con a, b i raggi dei cerchi base del segmento, il volume è espresso da V=πh (3a²+3b²+h²)/6. Settore sferico La parte di solido sferico limitata dalla superficie della s. e da due coni circolari aventi per vertice il centro della s. e uno stesso asse. Un settore sferico si può pensare ottenuto proiettando dal centro della s. una zona sferica oppure una calotta sferica (in questo caso uno dei due coni scompare). Indicando con h l’altezza della zona o della calotta e con R il raggio della s., il volume del settore sferico è dato da V=2πR²h/3. Spicchio sferico La parte di solido sferico compresa tra la s. e due semipiani uscenti da uno stesso diametro. Indicando con α l’angolo in gradi tra i due semipiani e con R il raggio della s., il volume dello spicchio è dato da V=πR³α/270. Triangolo sferico Poligono sferico con tre lati. Indicato con ε l’eccesso sferico del triangolo misurato in radianti, l’area S del triangolo è data da S=εR². Dunque, due triangoli di una stessa s. o di s. uguali hanno aree proporzionali ai rispettivi eccessi sferici. Zona sferica La parte di superficie sferica compresa tra due piani secanti paralleli. Indicando con h la loro distanza (altezza della zona) e con R il raggio della s., l’area della zona è S=2πRh.

La s. nella geometria analitica

Riferita la s. a un sistema monometrico di assi cartesiani ortogonali, detto C(x₀, y₀, z₀) il suo centro e indicato con R il suo raggio, si ricava per essa l’equazione:

[1] formula

dove x, y, z sono le coordinate di un punto generico P appartenente alla sfera. L’equazione [1] esprime che il quadrato della distanza CP uguaglia il quadrato del raggio. La [1] è un’equazione del tipo:

[2] formula

viceversa, ogni equazione del tipo [2] rappresenta una s. di centro C(−a/2, −b/2, −c/2) e raggio

La s. è perciò una particolare superficie del 2° ordine, cioè una quadrica caratterizzata dal fatto che nella sua equazione mancano i termini rettangolari (cioè i monomi in xy, xz, yz) e che i coefficienti dei termini in x2, y2, z2 sono tra loro uguali. Si osservi però che in geometria analitica si considerano come punti della s. anche le terne di numeri complessi che soddisfano la [1]: perciò la s. della geometria elementare non coincide con quella della geometria analitica, ma la prima è solo il luogo dei punti a coordinate reali della seconda. Aggiungendo i punti a coordinate complesse, la trattazione diviene più semplice e armonica; così, per es., la sezione di un piano e di una s. è sempre una circonferenza (reale o immaginaria); tutte le s. dello spazio hanno in comune una conica immaginaria all’infinito, loro comune intersezione con il piano improprio, e hanno come ulteriore intersezione un altro cerchio.

Funzioni sferiche

Importante categoria di funzioni omogenee e armoniche, cioè soluzioni dell’equazione di Laplace (➔ Laplace, Pierre-Simon de), comprendente come caso particolare le funzioni s. di Legendre

rispettivamente di prima e di seconda specie e, per n intero, i polinomi di Legendre (➔ Legendre, Adrien-Marie). Si tratta, in generale, di funzioni cui si perviene considerando le funzioni definite in un campo C di una superficie s., che sono soluzioni di una opportuna equazione differenziale e soddisfano determinate condizioni al contorno del campo C.

Astronomia

S. celeste Ipotetica superficie sferica di raggio grandissimo centrata nell’occhio dell’osservatore (che si può confondere, per lo più senza eccessivo errore, con il centro della Terra), sulla quale gli astri sembrano disposti. In particolare veniva chiamato s. ognuno dei 9 cieli che, contenuti l’uno nell’altro come s. concentriche di sempre maggior grandezza, costituivano, secondo la teoria tolemaica, l’universo ruotante intorno alla Terra. A causa del moto di rotazione della Terra intorno al proprio asse, la s. celeste infatti appare ruotare, con tutti gli astri, da Levante verso Ponente (moto diurno).

Biologia

Apparato della s. Complessa struttura citoplasmatica che compare durante la profase e scompare nella telofase mitotica e meiotica, formata dai centrioli, dall’astrosfera e dal fuso mitotico: la sua funzione principale è quella di determinare lo spostamento dei cromosomi durante l’anafase della divisione cellulare.