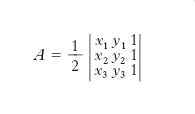triangolo
Matematica
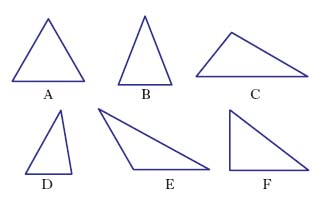
In geometria, figura piana limitata da 3 segmenti (lati del t.) che congiungono a due a due 3 punti non allineati (vertici del t.); è dunque un poligono di 3 lati. Rispetto ai lati si distinguono (fig. 1 A-C): t. equilatero (che ha 3 lati uguali), t. isoscele (che ha 2 lati uguali), t. scaleno (che ha tutti e i 3 lati diversi); rispetto agli angoli (fig. 1 D-F): t. acutangolo (che ha 3 angoli acuti), t. ottusangolo (che ha un angolo ottuso), t. rettangolo (che ha un angolo retto). Altro tipo di t. è il t. sferico (➔ sfera).
In un t. si chiama angolo interno ciascuno degli angoli racchiusi dai lati; si dice invece angolo esterno quello formato da un lato e dal prolungamento di uno dei due lati rimanenti. La somma degli angoli interni di un qualsiasi t. è sempre uguale a 2 angoli retti (cioè a 180°). Un angolo esterno è uguale alla somma degli angoli interni a esso non adiacenti. Si chiama altezza del t. relativa a un suo lato, il segmento di perpendicolare abbassata al lato considerato (o al suo prolungamento) dal vertice opposto. I tre lati soddisfano alla disuguaglianza triangolare («In un t. qualsiasi la somma di due lati è maggiore del terzo lato», o anche: «un lato è maggiore della differenza degli altri due»). L’angolo γ formato da due lati, a, b, si dice opposto al terzo lato, c. E così anche il vertice C, nel quale concorrono a e b, si dice opposto al lato c. L’angolo e il vertice opposti rispettivamente ad a e b si indicano con α, A, e β, B. Si ha che: in ogni t. a lato maggiore si oppone angolo maggiore, e viceversa; mentre se due lati sono uguali, lo sono anche gli angoli opposti, e viceversa (caso del t. isoscele).
Punti notevoli di un t. sono: baricentro (➔), circocentro (➔), excentro (➔ exinscritto, cerchio), incentro (➔), ortocentro (➔).
Criteri di uguaglianza e di similitudine
Due t. si dicono uguali (o congruenti) se hanno rispettivamente uguali tutti i lati e tutti gli angoli. Per affermare l’uguaglianza di due t. basta constatare l’uguaglianza dei seguenti loro elementi: a) 2 lati e l’angolo compreso; b) un lato e i 2 angoli a esso adiacenti; c) i 3 lati.
Due t. si dicono simili se hanno gli angoli ordinatamente uguali e i lati corrispondenti proporzionali. Per affermare che due t. sono simili basta constatare che: a) hanno angoli uguali; b) hanno uguale una sola coppia di angoli mentre i lati che comprendono l’angolo uguale sono proporzionali; c) hanno i lati proporzionali.
Area del triangolo
L’area A del t. è uguale alla metà del prodotto di un lato (preso come base) b per l’altezza h relativa a esso. In formule: A=bh/2; in forma trigonometrica è data da: A=(ab sen γ)/2, dove a e b sono due lati del t. e γ è l’angolo compreso; in funzione dei lati a, b, c e del semiperimetro p, è data da: A = √‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ p(p−a)(p−b)(p−c) (formula di Erone); altre espressioni trigonometriche dell’area, nelle quali intervengono tutti e tre gli angoli α, β, γ del t. sono: A=p2 tg(α/2) tg(β/2) tg(γ/2) e 8A3=a2b2c2 senα senβ senγ. Se x1, y1; x2, y2; x3, y3 sono le coordinate cartesiane ortogonali dei vertici, l’area (orientata) è data da:
Relazioni tra gli elementi di un triangolo
Dei 6 elementi (lati e angoli) di un t., 3 possono essere dati ad arbitrio, purché essi non siano tutti angoli e purché sia soddisfatta la disuguaglianza triangolare se si tratta dei 3 lati. Gli altri 3 possono allora essere ricavati dai 3 dati mediante formule della trigonometria (➔).
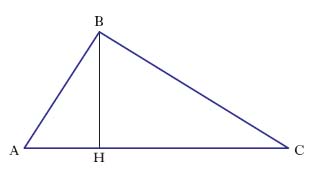
Per il teorema di Pitagora nel t. rettangolo ➔ Pitagora. I teoremi di Euclide si riferiscono a un t. rettangolo (fig. 2) e si enunciano: 1) in un t. rettangolo un cateto rappresenta il medio proporzionale tra l’ipotenusa e la sua proiezione sull’ipotenusa; si ha, per es., che: AC‾‾‾:AB‾‾‾=AB‾‾‾:AH‾‾‾. 2) In un t. rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei cateti sull’ipotenusa; così si ha che: AH‾‾‾:BH‾‾‾=BH‾‾‾:HC‾‾‾.
Anatomia
In anatomia topografica, zona delimitata da formazioni anatomiche in modo da ricordare la forma di un t. geometrico: t. di Farabeuf, nella parte superiore del collo, delimitato dalla vena giugulare interna, dalla vena facciale e dal nervo ipoglosso; t. della taglia, delimitato dal profilo laterale del torace e del fianco (che formano 2 lati del t.) e dal profilo mediale dell’arto superiore, quando si consideri il corpo in posizione di ‘attenti’.
Il termine triangolare è riferito a formazioni anatomiche che hanno pressoché forma di t.: fossetta triangolare, nel padiglione auricolare; muscolo triangolare del labbro, quello che dal bordo inferiore della mandibola si porta all’angolo della bocca; muscolo triangolare dello sterno, quello che dalla faccia posteriore dello sterno si porta alle prime coste ecc.
Astronomia
In astronomia sferica, t. astronomico o t. fondamentale, il t. PAZ sulla sfera celeste avente per vertici il polo celeste P, lo zenit dell’osservatore Z e la posizione di un astro A. La considerazione di questo t. trova impiego in numerosissimi problemi di astronomia sferica (problemi del moto diurno, sorgere e tramonto degli astri ecc.) e nautica (in questa il t. prende a preferenza il nome di t. di posizione). Triangolo (lat. scient. Triangulum) Piccola costellazione del cielo boreale, tra Perseo e Andromeda, così denominata perché le sue tre stelle principali sembrano formare un t. isoscele. La stella più brillante (β Trianguli) ha magnitudine 3. Nella regione del Triangolo cade la galassia spirale M33 (o NGC 598). Triangolo australe (lat. scient. Triangulum australe) Piccola costellazione del cielo australe, a S della Norma, introdotta da J. Bayer nel 1603. Il nome le fu dato dai navigatori del 16° secolo. La sua stella principale ha magnitudine 1,9.
Fisica
In cinematica dei moti relativi, t. delle velocità, quello che ha per lati i vettori della velocità relativa, della velocità di trascinamento e della velocità assoluta di un corpo (somma delle prime due): per es., nella navigazione aerea e in quella marittima la velocità assoluta (o effettiva) si ottiene sommando alla velocità relativa quella del vento o della corrente.
Musica
Strumento musicale a percussione, costituito da una sottile sbarra d’acciaio ripiegata a t., che, tenuto sospeso, viene percosso mediante una bacchetta, anch’essa d’acciaio, producendo un suono di timbro argentino, di altezza indeterminata (ma acuta), di risonanza penetrante e persistente.