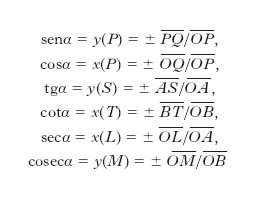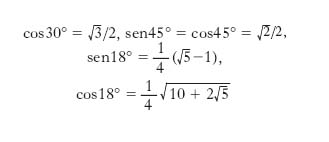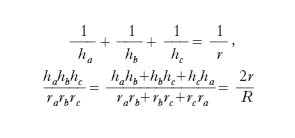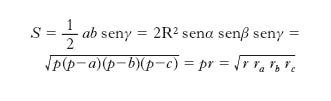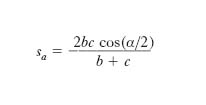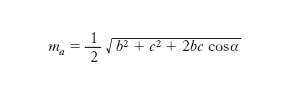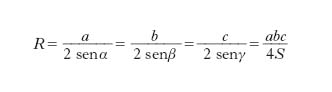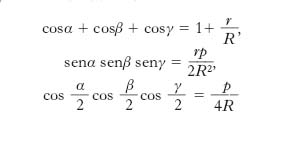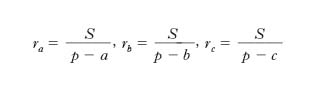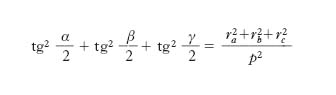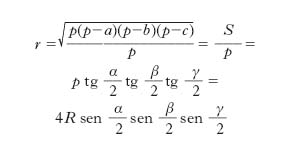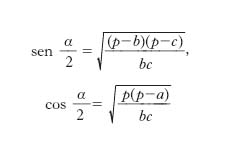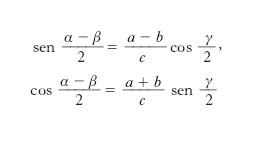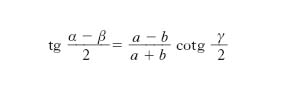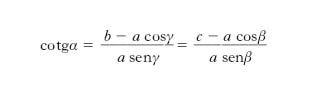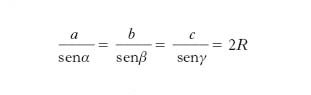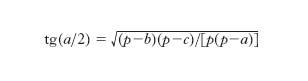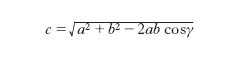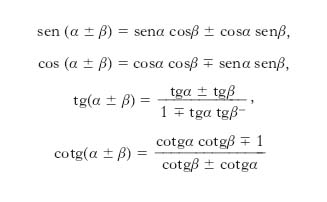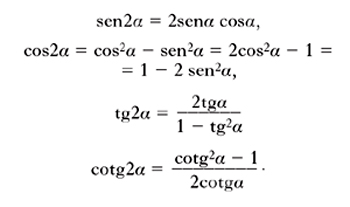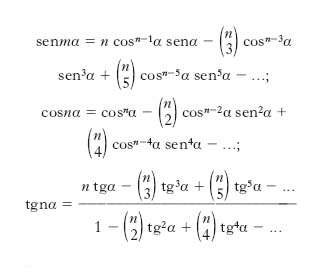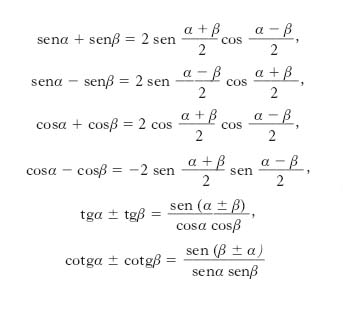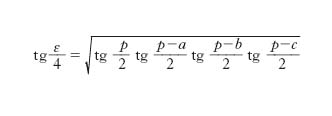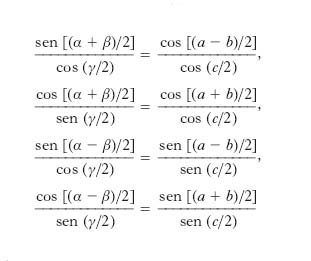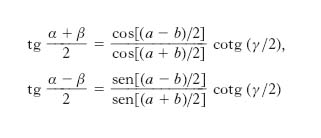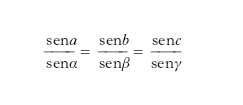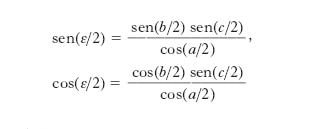trigonometria

Enciclopedia on line

In senso stretto, quella parte della matematica che si propone di calcolare i valori di tutti gli elementi (lati e angoli) di un triangolo, quando siano noti tre di essi (tra cui almeno un lato); più in generale, rientrano nella t. tutte le questioni collaterali, quali lo studio delle funzioni trigonometriche, la loro tabulazione ecc.

Funzioni trigonometriche

fig. 1

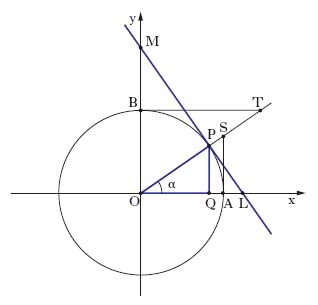
Si chiamano funzioni trigonometriche (o circolari) di un angolo α le funzioni senα, cosα, tgα, cotgα, secα, cosecα, da leggersi rispettivamente seno di α, coseno di α, tangente di α, cotangente di α, secante di α, cosecante di α. Considerato un cerchio trigonometrico (cioè un cerchio di raggio unitario sulla cui circonferenza sia fissato un punto da assumersi come inizio degli archi e un verso, di solito quello antiorario), avente come centro l’origine O di un sistema di assi cartesiani x, y (fig. 1), le funzioni trigonometriche dell’angolo α sono definite così: introdotti i punti P, Q, S, T, L, M si ha:

Le 6 funzioni trigonometriche sono collegate da varie relazioni, tra cui (esprimendo gli angoli in gradi sessagesimali):

cos(90°−α) = senα, sen(90°−α) = cosα,

tgα = senα/cosα, cotgα = 1/tgα,

secα = 1/cosα, cosecα = 1/senα,

sen²α + cos²α = 1.

Tutte le funzioni trigonometriche sono periodiche: hanno periodo uguale a 180° le funzioni tgα e cotgα, uguale a 360° le altre. È inoltre

sen(180°−α) = senα, cos(180°−α) =

= − cosα,

tg(180°−α) = − tgα,

sen(180°+α) = −senα, cos(180°+α) =

= − cosα,

tg(180°+α) = tgα,

sen(360°−α) = −senα, cos(360°−α) =

= cosα,

tg(360°−α) = −tgα.

Le formule precedenti consentono di ricondurre il calcolo delle funzioni trigonometriche di un qualsiasi angolo al caso di angoli compresi tra 0° e 90° (riduzione al primo quadrante) o, addirittura, tra 0° e 45° (riduzione al primo ottante). Si ha, per es., cos300°=cos(360°−60°)=cos60°=cos(90°−30°)=sen30°=1/2; alcuni altri valori notevoli delle funzioni trigonometriche nel primo ottante sono:

fig. 2

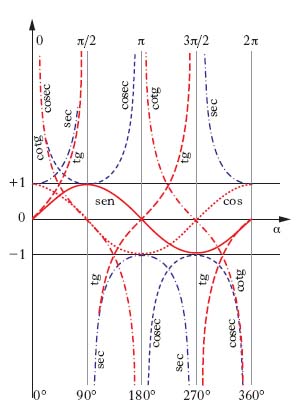
In fig. 2 sono indicati, limitatamente all’intervallo [0°, 360°], i diagrammi delle sei funzioni trigonometriche; da essa si rileva che senα e cosα variano nell’intervallo chiuso [−1, 1], secα e cosecα assumono valori in (−∞, −1] e [1, +∞), mentre tgα e cotgα acquistano qualsiasi valore reale. Inoltre, i diagrammi di senα, cosα, tgα, cotgα presentano un flesso in ogni attraversamento dell’asse α; tgα, cotgα, secα, cosecα hanno asintoti paralleli all’asse delle ordinate. Funzioni trigonometriche inverse sono le funzioni arcoseno, arcocoseno, arcotangente, arcocotangente, arcosecante, arcocosecante (in simboli: arcsen, arccos, arctg, arccot, arcsec, arccosec), inverse rispettivamente delle funzioni seno, coseno, tangente, cotangente, secante, cosecante. Sono funzioni a infiniti valori, in quanto inverse di funzioni periodiche. Funzioni trigonometriche nel campo complesso sono funzioni complesse di variabile complessa che godono di molte proprietà delle funzioni trigonometriche nel campo reale. Una possibile definizione è basata sulla formula di Eulero:

e^x^+iy=e^x (cosy+i seny),

da cui si deduce

senz=(e^iz−e^−iz)/2i, cosz=(e^iz+e^−iz)/2,

ponendo poi

tgz=senz/cosz=1/cotgz.

Un’altra definizione si basa sull’osservazione che gli sviluppi in serie (➔) di senx e di cosx convergono anche per qualsiasi valore complesso della variabile. Per le funzioni trigonometriche nel campo complesso valgono ancora le formule di addizione, di moltiplicazione ecc.; non valgono, invece, le proprietà delle funzioni trigonometriche nel campo reale che si esprimono mediante disuguaglianza: così non è vero, nel campo complesso, che |senα| e |cosα| sono inferiori o uguali a uno.

T. piana

fig. 3

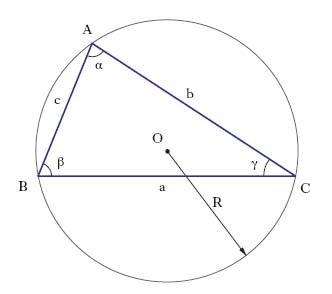
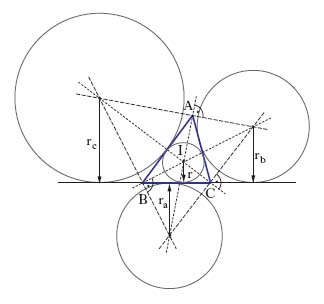
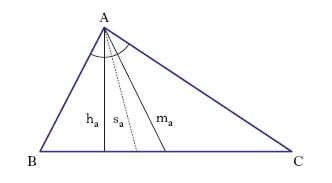
Nel seguito sono elencate, alfabeticamente entro ogni gruppo, le formule che danno gli elementi più notevoli di un triangolo, e poi altre formule e teoremi sui triangoli. Con riferimento al triangolo ABC, si sono indicati rispettivamente (fig. 3, 4, 5) con α, β, γ,

gli angoli convessi BAC⋀, ABC⋀, ACB⋀, e

con a, b, c i lati BC, AC, AB; il perimetro è indicato con 2p, mentre O e R denotano il centro e il raggio del cerchio circoscritto, e così I e r centro e raggio del cerchio inscritto; con r_a si è indicato il raggio del cerchio exinscritto contenuto nell’angolo α (similmente r_b e r_c); infine, h_a, m_a, s_a indicano rispettivamente l’altezza, la mediana e la bisettrice uscenti dal vertice A. Segue, sempre in ordine alfabetico, un elenco di altre formule e identità non necessariamente relative a triangoli.

Teoremi e relazioni principali

Altezze di un triangolo

L’altezza h_a relativa al lato a è espressa da h_a=b sen γ =c senβ. Analogamente per h_b e h_c. Si hanno inoltre le relazioni

Area di un triangolo

È data da

si ha inoltre

16S² = (a² + b² +c²)² − 2(a⁴ + b⁴ +c⁴).

Bisettrici di un triangolo

La bisettrice s_a relativa al vertice A è data da

Mediane di un triangolo

La mediana relativa al lato a è data da

Raggio del cerchio circoscritto a un triangolo

Si ha

Altre relazioni in cui interviene R sono:

Raggi dei cerchi exinscritti a un triangolo

Sono dati da

la somma r_a+r_b+r_c è uguale a 4R+r. Vale inoltre la relazione:

Raggio del cerchio inscritto in un triangolo

Ha le seguenti espressioni

Un collegamento tra r e R è costituito dal teorema di Chapple: |OI|²=R(R−2r), dove O e I sono i centri dei cerchi circoscritto e inscritto. Se ne deduce che è sempre R≥2r e anzi R=2r solo per un triangolo equilatero.

Formule di Briggs

Sono

e le altre 4 che se ne deducono permutando circolarmente α, β, γ e a, b, c. Formule di Delambre (o di Mollweide) Gruppo di 6 formule di cui le prime due sono

e le altre si ottengono con permutazione circolare.

Formule di Nepero (o di Pitisco-Nepero)

Sono tre formule, una delle quali è

e le altre due si ottengono con permutazione circolare.

Teorema di Carnot (o del coseno)

È un teorema che generalizza il teorema di Pitagora e che è espresso dalla relazione

a² = b² + c² − 2bc cosα

(e dalle analoghe per b² e c²).

Teorema delle cotangenti

È dato dalla formula

e dalle analoghe per cotgβ e cotgγ, ottenute con permutazione circolare.

Teorema delle proiezioni

È dato dalla formula

a=b cosγ+c cosβ,

e dalle analoghe per b e per c, ottenute con permutazione circolare.

Teorema dei seni

È espresso dalle uguaglianze

Risoluzione di un triangolo qualsiasi

Si distinguono 4 casi: a) dati i tre lati a, b, c, gli angoli si possono dedurre dal teorema di Carnot o dalle formule di Briggs: così si ha, per es., cosα=(b²+c²−a²)/2bc, oppure

b) dati due lati a, b e l’angolo compreso γ, il lato c si può ottenere partendo dal teorema di Carnot, cioè si ha:

e successivamente, per il teorema dei seni, senα=(a/c) senγ, senβ=(b/c) senγ; c) dati due lati a, b e l’angolo opposto a uno di essi, per es., l’angolo α opposto ad a, si ottiene (nel caso esistano soluzioni) senβ=(b/a)senα, γ=180°−(α−β), c=a[sen(α+β)]/senα; d) dati un lato a e due angoli β e γ adiacenti ad a, si ha: α=180°−(β+γ), b=a senβ/sen(β+γ), c=a senγ/sen(β+γ); se invece sono dati l’angolo opposto α e uno degli angoli adiacenti, per es., β, si avrà: γ=180°−(α+β), b=a senβ/senα, c=a sen(α+β)/senα.

Risoluzione di un triangolo rettangolo

Per un triangolo in cui a è l’ipotenusa, b e c sono i cateti, β e γ gli angoli opposti a questi, si ha: b=a senβ, b=a cosγ, b=c tgβ, b=c ctgγ, c=a senγ, c=a cosβ, c=b tgγ, c=b ctgβ.

Altre formule e identità trigonometriche

Formule di addizione e sottrazione

Esprimono le funzioni circolari degli angoli α+β (e α−β) mediante quelle degli angoli α e β. Esse sono

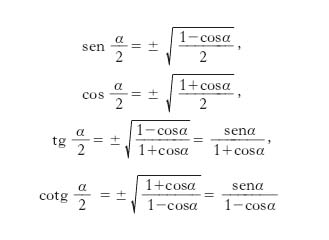
Formule di bisezione

Esprimono le funzioni circolari di α/2 a partire da quelle di α. Esse sono

Formule di duplicazione

Esprimono le funzioni dell’angolo 2α a partire da quelle di α. Esse sono

Sono spesso utili anche le relazioni

Formule di moltiplicazione

Esprimono sennα, cosnα, tgnα mediante le funzioni circolari di α. Esse sono

In tutte le formule ci si deve arrestare quando si arriva a un coefficiente binomiale in cui il numero scritto inferiormente supera n.

Formule di prostaferesi

Trasformano in un prodotto la somma di due funzioni circolari. Le più importanti sono

T. sferica

fig. 6I

Caratteri generali

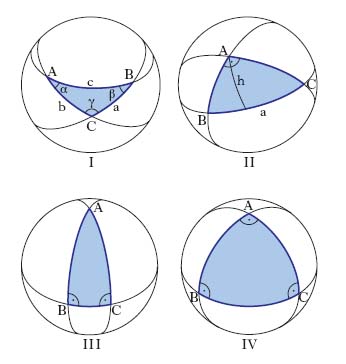
La t. sferica tratta delle relazioni tra gli elementi di un triangolo sferico (➔ sfera). Siano A, B, C, i vertici di un triangolo sferico (fig. 6I), a, b, c i lati e α, β, γ, gli angoli rispettivamente in A, B, C. In un triangolo siffatto ogni lato e angolo (misurando lati e angoli in gradi sessagesimali) ha un’ampiezza compresa tra 0° e 180°, estremi esclusi. La t. sferica presenta talune analogie con quella piana (per es., in un triangolo sia piano sia sferico un lato è minore della somma e maggiore della differenza degli altri due); vi sono però differenze essenziali. Se ne ricordano due: a) mentre in un triangolo piano la somma degli angoli vale 180°, in un triangolo sferico tale somma supera sempre 180° per una quantità che si chiama eccesso sferico del triangolo. b) Non esistono equazioni algebriche che legano tra di loro i lati e gli angoli di un triangolo sferico, ma si possono stabilire delle relazioni algebriche tra le funzioni circolari dei lati e degli angoli in modo che dati tre qualunque dei sei elementi (anche tutti gli angoli), si possono determinare gli altri tre. Non esistono perciò sulla sfera triangoli simili, nel senso che due triangoli simili sono addirittura uguali. Estensioni della t. sferica sono dovute ad A.F. Möbius (con la considerazione di triangoli sferici più generali, detti triangoli di Möbius, nei quali i lati e gli angoli sono compresi tra 0 e 2π), E. Study, F. Klein ecc.

Teoremi e formule principali

Area di un triangolo sferico

In base al teorema di Cavalieri l’area di un triangolo sferico è uguale a quella di un fuso appartenente alla stessa sfera e avente sezione normale uguale alla metà dell’eccesso sferico del triangolo. Esprimendo gli angoli α, β, γ in radianti si ha quindi S=R2(α+β+γ−π), dove R è il raggio della sfera su cui giace il triangolo.

Eccesso sferico di un triangolo

È l’angolo ε espresso da α+β+γ−180°. Una formula che dà l’eccesso sferico in funzione dei lati è

con p=(a+b+c)/2.

Formule di Cagnoli

Sono senb senc + cosb cosc cosa = senβ senγ - cosβ cosγ cosα,

e le altre che si ottengono con sostituzioni circolari su a, b, c e su α, β, γ.

Formule di Delambre

Sono

e le analoghe. Formule di Nepero si ottengono dividendo membro a membro le formule di Delambre

Formule di Nepero-Borda

Esprimono gli angoli di un triangolo sferico in funzione dei lati. Posto al solito, a+b+c=2p esse si scrivono

e le analoghe permutando circolarmente le lettere. Se i lati a, b, c sono molto piccoli il triangolo sferico può, in prima approssimazione, considerarsi un triangolo piano; risultando senb∼b, senc∼c ecc., le formule di Nepero-Borda si riducono allora alle formule di Briggs della t. piana.

Teorema del coseno (o di Eulero)

Si ha

cosa=cosb cosc+senb senc cosα

e analogamente per b e c.