circonferenza
In geometria, curva piana, luogo dei punti equidistanti da un punto fisso O, detto centro della c.; la superficie piana da essa racchiusa è il cerchio. La distanza costante dal centro a un punto qualsiasi della c. si chiama raggio; il doppio di essa, diametro. Molte nozioni e proprietà della c. sono intimamente legate a quelle del cerchio (➔). Una c. è determinata allorché sono dati 3 punti non allineati, per i quali essa debba passare. La sua lunghezza vale 2 π r, ove r è il raggio; la lunghezza l di un arco, il cui angolo al centro sia α, vale l=r α se α è misurato in radianti, l=π r α /180° se α è misurato in gradi sessagesimali.
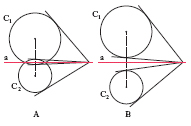
Tra le proprietà geometriche della c. una delle più notevoli è la cosiddetta proprietà isoperimetrica: fra tutte le linee chiuse di data lunghezza la c. è quella che racchiude area massima (oppure: la c. è la linea di lunghezza minima tra quelle che racchiudono un’area data). Date due c., C1, C2, si chiama loro asse radicale la retta a costituita dai punti che hanno la stessa potenza rispetto a esse, cioè la retta luogo dei punti tali che i segmenti di tangente condotti dai punti stessi alle due c. sono uguali (fig. 1).
La ciclotomia, cioè la divisione della c. in n parti uguali, si identifica con il problema della costruzione dei poligoni regolari (di n lati) iscritti nella c. e si può far dipendere dalla risoluzione, nel campo complesso, dell’equazione xn−1=0, detta equazione ciclotomica (➔ anche poligono). Usando solo la riga e il compasso (cioè, con costruzioni elementari), il problema si può risolvere (K.F. Gauss) solo quando n sia scomponibile nel prodotto di una potenza di 2 per fattori primi della forma 2p+1, nel qual caso l’equazione xn−1=0 è risolubile per radicali quadratici. Il problema della ciclotomia è perciò risolubile, usando solo la riga e il compasso, per n=3, 4, 5, 6, 8, 10, 12, 15, 17 ecc.; irresolubile per n=7, 9, 11, 13 ecc.
La rettificazione della c. è la costruzione, a partire dal diametro (o dal raggio), di un segmento avente lunghezza uguale a quella della circonferenza. I geometri greci (in particolare Archimede) si avvicinarono alla soluzione, per approssimazioni successive, nel seguente modo. Le misure dei perimetri dei poligoni regolari di 6, 12, 24 ecc. lati, iscritti e circoscritti nella c., offrono evidentemente due successioni, l’una crescente, l’altra decrescente, che approssimano (l’una per difetto, l’altra per eccesso) la c. rettificata. Per questa via, Archimede riuscì a dare un valore approssimato a meno di due millesimi del rapporto (che già era stato dimostrato essere lo stesso per qualsiasi c.) tra la c. e il diametro, cioè del numero π; essendo quest’ultimo un irrazionale trascendente, la rettificazione della c. non è problema risolubile con costruzioni elementari cioè usando solo riga e compasso (➔ anche pi).
In coordinate cartesiane ortogonali, l’ equazione della c. di centro nel punto (α,β) e raggio r si scrive:
(x − α)2 + (y − β)2 = r2;
essendo l’equazione di 2° grado, le c. rientrano tra le coniche. Una c. qualunque interseca la retta impropria del piano in due punti immaginari coniugati che per questo si chiamano i punti ciclici (la proprietà di passaggio per i punti ciclici è anzi caratteristica: ogni conica passante per i punti ciclici è una c.); ciò fa sì che il fascio di coniche individuato da due c. è tutto formato da c.: è un fascio di circonferenze. Facendo variare, in tutto lo spazio, il piano della c., i punti ciclici descrivono una conica immaginaria detta c. assoluta o cerchio assoluto.
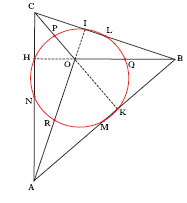
Dato un triangolo qualsiasi (ABC, in fig. 2), la c. dei 9 punti (o c. di K.W. Feuerbach) è la c. che passa per i punti medi L, M, N dei tre lati del triangolo, per i piedi I, K, H delle tre altezze, e per i punti medi P, Q, R dei segmenti di queste compresi tra l’ortocentro O e i rispettivi vertici.