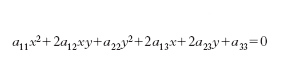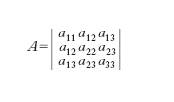conica
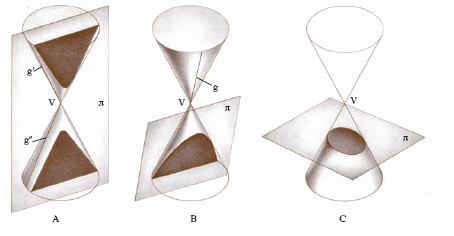
Curva che si ottiene segando un cono circolare (retto od obliquo) con un piano. Il cono va pensato come luogo di rette, e non di semirette, uscenti dal vertice V, cioè costituito, come si usa dire nel linguaggio elementare, da due ‘semiconi’ opposti al vertice. Si presentano tre diversi casi. Se il piano, π (fig. 1A), è parallelo a due generatrici, g′ e g″, queste dividono la superficie del cono in due parti: le generatrici dell’una parte sono incontrate da π da una medesima banda rispetto al vertice (in un ‘semicono’), le altre dalla banda opposta; si ha come intersezione un’iperbole. Se π (fig. 1B) è parallelo a una sola generatrice, g, incontra tutte le altre da una stessa parte di V: la sezione è una parabola. Se π (fig. 1C) non è parallelo ad alcuna generatrice (di modo che le sega tutte da una stessa parte del vertice), la curva sezione è un’ellisse, in particolare una circonferenza. Se il piano π passa per il vertice V, l’intersezione di esso con il cono si riduce a una coppia di rette (che possono essere reali e distinte, reali e coincidenti oppure complesse coniugate; i tre casi sono rispettivamente in analogia con i casi illustrati). Nella famiglia delle c. vanno quindi incluse anche le coppie di rette complanari, che si suole chiamare c. spezzate o degeneri.
La teoria elementare delle c. concepite come sezioni piane di un cono è stata ampiamente sviluppata nell’antichità greca, da Menecmo (4° sec. a.C.) discepolo di Eudosso, ad Archimede, fino alla grande opera di Apollonio di Perge, in 8 libri, nella quale si può dire che tale teoria trovi il suo assetto completo e definitivo. In seguito lo studio delle c. è stato condotto dal punto di vista della geometria proiettiva piana: ne è stato iniziatore, intorno al 1650, G. Desargues; la sistemazione definitiva della teoria si è avuta, nella prima metà del 19° sec., per opera di J.-V. Poncelet, e poi di J. Steiner e K.G.Ch. Staudt. Successivamente ha preso sviluppo la teoria delle c. da un punto di vista analitico; questa via ha portato a varie generalizzazioni della nozione di c., per es. alla nozione di c. in un piano lineare (➔ piano), sopra un campo qualsiasi.
Con la geometria proiettiva, la teoria delle c. ha raggiunto una profonda unità e una singolare semplicità ed eleganza. Così, per es., risulta sempre possibile passare, mediante operazioni di proiezione e sezione, da una data c. a un’altra qualsiasi c. data (si parla di c. non degeneri). Giacché nella geometria proiettiva si identificano le figure che possono trasformarsi l’una nell’altra mediante proiezioni e sezioni, si conclude che le c. non degeneri e fornite di punti reali sono tutte proiettivamente identiche; oltre a queste, la classificazione proiettiva delle c. considera altri 4 tipi: le c. non degeneri ma sprovviste di punti reali, quelle degeneri in due rette reali, quelle degeneri in due rette immaginarie coniugate, quelle formate da una retta contata due volte ( c. doppiamente degeneri). La sostanziale unità delle c. si comprende dalla loro generazione proiettiva: ogni c. non degenere è il luogo dei punti di incontro di raggi corrispondenti di due fasci proiettivi, non prospettivi e non sovrapposti ( teorema di Steiner).
Dal punto di vista della geometria affine le c. non degeneri si distinguono in ellissi, parabole, iperboli se hanno rispettivamente nessun punto reale, un punto reale, due punti reali all’infinito. Questa classificazione si può anzi applicare anche alle c. degeneri. Si definisce poi centro di una c. il polo della retta all’infinito, e diametro ogni retta per il centro.
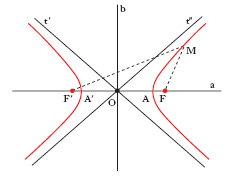
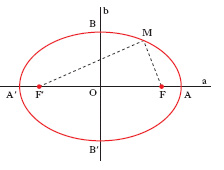
Le proprietà metriche di una c. sono quelle che restano invariate rispetto a un qualsiasi movimento; tutte le proprietà proiettive e affini sono anche proprietà metriche. I principali enti geometrici associati a proprietà metriche in senso stretto delle c. sono l’asse, i vertici, i fuochi, le direttrici. L’ asse è un diametro la cui retta di appartenenza è di simmetria ortogonale per la c.; nell’iperbole e nell’ellisse vi sono due assi ortogonali (a e b nelle fig. 2 e 4), in una parabola vi è un solo asse (a nella fig. 3), mentre in una circonferenza ogni diametro è un asse. I vertici sono i punti comuni alla c. e a un asse: l’iperbole ha due vertici reali (A e A′ nella fig. 2) e due immaginari, la parabola ha un vertice al finito (V nella fig. 3) e un altro all’infinito, l’ellisse ha quattro vertici reali al finito (A, A′, B, B′ nella fig. 4), mentre nella circonferenza ogni punto può considerarsi vertice. I fuochi sono i punti tali che due rette ortogonali passanti per essi siano coniugate rispetto alla c.; essi non appartengono alla c., anzi sono interni a essa: le rette tangenti alla c. passanti per un fuoco sono rette isotrope. Un’ellisse possiede due fuochi reali (F, F′) situati sull’asse maggiore (a), detto perciò anche asse focale, e due fuochi immaginari sull’asse minore (b); un’iperbole ha due fuochi reali (F, F′) sull’asse trasverso (a) e due immaginari sull’asse non trasverso (b). Una parabola ha un solo fuoco (F), situato sull’asse (a). Anche una circonferenza ha un solo fuoco, coincidente con il centro. Le direttrici di una c. sono le polari dei fuochi. A ogni fuoco reale corrisponde una direttrice pure reale, esterna alla c. e perpendicolare all’asse focale. La parabola ha una sola direttrice (d), perpendicolare all’asse; anche la circonferenza ha una sola direttrice, che è la retta all’infinito.
Alle stesse curve prima definite come sezioni c. si può pervenire con molte possibili costruzioni di carattere elementare. Una c. (che non sia una circonferenza) è il luogo dei punti le cui distanze da un punto fisso (detto fuoco) e da una retta fissa (direttrice relativa al fuoco considerato) stanno in rapporto costante. Tale rapporto costante si chiama eccentricità della c. e si suole indicare con e: a seconda che e〈1, e=1, e>1, si tratta di un’ellisse o di una parabola o di un’iperbole (dall’una all’altra specie di c. si passa così per variazione continua dell’eccentricità). In particolare, l’iperbole (fig. 2) è il luogo dei punti M le cui distanze da due punti fissi F, F′ (fuochi) hanno differenza costante in valore assoluto; la parabola (fig. 3) risulta essere luogo dei punti M equidistanti da un punto F (il fuoco) e da una retta d (direttrice); l’ellisse (fig. 4) è il luogo dei punti M le cui distanze da due punti fissi F, F′ (fuochi) hanno somma costante.
Le c. si definiscono, dal punto di vista analitico, come le curve rappresentate, in coordinate cartesiane, da un’equazione algebrica di 2° grado:
L’equazione di una c. dipende da sei coefficienti: ma ciò che conta è il rapporto di cinque di essi al sesto (in quanto è lecito moltiplicare o dividere il primo membro dell’equazione per una costante). Essendo cinque i coefficienti essenziali, si ha che per cinque punti generici di un piano passa una c. e una soltanto. La teoria delle c. (la loro classificazione, le loro proprietà ecc.) può essere sviluppata in modo completo con i metodi analitici. Per es., una c. è non degenere quando e soltanto quando il determinante A dei coefficienti della sua equazione, il cosiddetto invariante cubico,
è diverso da zero; se poi sono nulli tutti i minori di ordine due della matrice considerata (ossia essa ha caratteristica 1), la c. è costituita da una retta contata due volte e la sua equazione può ridursi al tipo
(ax+by+c)2=0.
Inoltre, una c. è ellisse, parabola o iperbole a seconda che l’invariante quadratico a11a22 − a212 sia maggiore, uguale o minore di zero (➔ invariante) ecc.