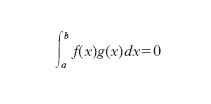ortogonale

In geometria elementare si dice di due enti che formano tra loro un angolo retto.

fig. 1 A

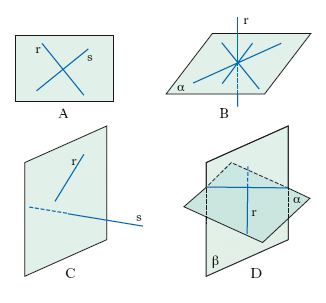
Due rette r, s del piano si dicono o. (o perpendicolari) se si intersecano formando quattro angoli retti (fig. 1 A); una retta r dello spazio si dice o. (o perpendicolare) a un piano α se incontra il piano in un punto ed è perpendicolare a tutte le rette uscenti da questo punto e giacenti nel piano (fig. 1 B). Due rette dello spazio (per es., r, s in fig. 1 C) si dicono o. quando esiste un piano passante per una di esse e perpendicolare all’altra; due piani dello spazio (α, β in fig. 1 D) si dicono o. (o perpendicolari) se esiste in uno di essi una retta r o. all’altro. Quando si fa riferimento ai punti impropri delle rette considerate (direzioni) e alle rette improprie dei piani considerati (giaciture) si parla anche di direzioni o., di giaciture o., di direzione o. a una giacitura. Non sempre i termini o. e perpendicolare sono usati come sinonimi; infatti perpendicolare ha talora il significato di o. e incidente. In entrambi i significati si usa anche l’aggettivo normale. La nozione di ortogonalità si generalizza in vari sensi.

In un iperspazio euclideo di dimensione r una retta e un iperpiano si dicono o. se la retta è incidente l’iperpiano in un punto e se risulta o. a tutte le rette dell’iperpiano uscenti da tale punto; due rette si dicono o. se esiste un iperpiano per l’una che sia o. all’altra; due spazi subordinati di dimensioni qualsiasi si dicono debolmente o. se in uno di essi esiste una retta o. a tutte le rette dell’altro e invece fortemente o. se ogni retta di ciascuno di essi è o. a ogni retta dell’altro.

fig. 2

fig. 3 A

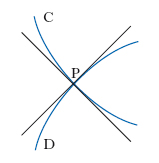
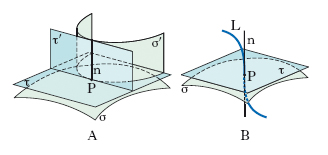
Due linee, C, D, aventi un punto comune P e ivi dotate di tangente si dicono o. in quel punto se sono o. le loro tangenti in quel punto (fig. 2); per es., sono o. nei loro punti d’incontro, una circonferenza e una retta passante per il suo centro. Il concetto si estende a due superfici σ, σ′ (fig. 3 A), o a una linea L e a una superficie σ (fig. 3 B), che si dicono o. in un punto P quando passano entrambe per quel punto e quando i due piani τ e τ′ tangenti in esso (o rispettivamente la retta n tangente alla linea e il piano τ tangente alla superficie in quel punto) sono tra loro ortogonali. La nozione si estende analogamente alle varietà di dimensione superiore, mediante la considerazione degli spazi tangenti. Dicesi anche di due funzioni, il cui integrale esteso a tutto lo spazio della variabile è uguale a zero.

Le condizioni di ortogonalità sono le relazioni analitiche che esprimono la condizione affinché due enti siano o. tra loro. Il caso più elementare è quello di due rette nel piano, assegnate, rispetto a un riferimento cartesiano o., mediante le loro equazioni ax+by+c=0, a′x+b′y+c′=0: la condizione di ortogonalità è espressa dalla relazione aa′+bb′=0. Per due rette nello spazio, aventi parametri direttori l, m, n e rispettivamente l′, m′, n′, la condizione di ortogonalità è ll′+mm′+nn′=0. Analogamente, due vettori si dicono o. se è nullo il loro prodot;to scalare; due funzioni f(x), g(x), definite in un intervallo (a, b), e che per semplicità supponiamo ivi continue, si dicono

o. nell’intervallo se si ha

Il termine o. è usato in molti altri casi nei quali interviene in maniera essenziale il concetto di ortogonalità o una coppia (o più coppie) di enti ortogonali. Per es., è detto gruppo o., quello delle matrici quadrate o. (➔ matrice) di ordine n a elementi reali, composte con il prodotto righe per colonne. Esso si indica con il simbolo O_n e dipende da n(n−1)/2 parametri: per n≥3 non è abeliano. Da un punto di vista geometrico O_n rappresenta le rotazioni dello spazio euclideo n-dimensionale E_n attorno a un punto di E_n. Si indica poi con O⁺_n il sottogruppo di O_n costituito dalle sole rotazioni dirette.