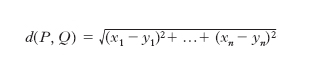iperspazio

In matematica, spazio a più dimensioni; il numero di queste si indica generalmente con n, nel qual caso si parla anche di spazio di dimensione n; poiché lo spazio ordinario è a tre dimensioni, in senso più ristretto i. è uno spazio di dimensione n>3. La nozione di i. può sembrare legata a costruzioni artificiose; nasce invece spontaneamente da problemi nei quali viene naturale di considerare entità variabili che dipendono da un numero di parametri anche molto grande. I. euclideo, di dimensione n I punti di questo i. sono le n-ple ordinate di numeri (x₁, ..., x_n) reali o complessi (rispettivamente si ha l’i. euclideo reale o complesso), detti coordinate del punto stesso; la sua struttura è quella che si ottiene trasportando la struttura di spazio metrico dell’ordinario spazio euclideo a tre dimensioni, e ciò viene fatto valendosi dello strumento analitico. Così, si definisce come iperpiano (di dimensione n−1) dell’i. il luogo dei punti dell’i. le cui coordinate soddisfano un’equazione lineare del tipo: a₁x₁+a₂x₂+...+a_nx_n = 0; si definisce come ipersuperficie una varietà avente dimensione n−1; si definiscono gli spazi lineari di dimensione n−2, ... fino alle rette, di dimensione 1, mediante intersezione di due o più iperpiani; si assume come distanza tra due punti P (x₁, ..., x_n) e Q (y₁, ..., y_n) la quantità

si definisce ipersfera l’insieme dei punti P aventi, da un punto C (c₁, c₂, ..., c_n), detto centro dell’i., distanza minore o uguale a una quantità prefissata r (raggio dell’i.). In modo analogo si possono poi definire gli angoli, il parallelismo, la perpendicolarità e generalizzare le altre nozioni valide nella geometria ordinaria, in modo da sviluppare una ‘geometria euclidea’ in un i. di dimensione n.

I. proiettivo, di dimensione n I suoi punti sono le (n+1)-ple (x₀, x₁, ..., x_n) non nulle omogenee, definite cioè a meno di un fattore di proporzionalità. Gli enti e le nozioni della geometria proiettiva vengono anche qui introdotti, per via analitica, sul modello della geometria proiettiva dello spazio ordinario. Così, si introducono le nozioni di iperpiano, di ipersuperficie di ordine qualunque r (luogo dei punti che soddisfano un’equazione omogenea di grado r; in particolare le iperquadriche sono di ordine 2), di proiettività (tra due i. distinti o coincidenti) ecc.

Lo studio di questi spazi a più dimensioni appare, almeno a priori, equivalente allo studio puramente analitico dei sistemi a n (oppure n+1) incognite: tuttavia, l’uso sistematico del linguaggio e delle nozioni proprie della geometria ha il vantaggio di attribuire a problemi e a proprietà analitiche una maggiore concretezza e una più viva evidenza.