luogo

Astronomia

Posizione che un astro ha sulla sfera celeste e che è espressa mediante le sue coordinate. Si chiama: l. apparente, se la determinazione delle coordinate è fatta correggendole soltanto l’effetto della rifrazione atmosferica; l. vero, se si tiene conto anche dell’aberrazione; l. medio, se si considera anche l’effetto della nutazione terrestre; in ognuno dei tre casi, l. geocentrico, o eliocentrico, a seconda che le coordinate siano geocentriche oppure eliocentriche; l. topocentrico (per gli oggetti celesti più vicini: Luna, pianeti, comete), se le coordinate sono riferite alla posizione dell’osservatore sulla superficie della Terra.

Filosofia

Nella retorica e nella logica, già in Aristotele sono detti luoghi (gr. τόποι) gli schemi formali mediante i quali sia possibile ricercare le premesse su cui poggia l’argomentazione probatoria. Oltre che nei Topici, Aristotele usa il termine anche nella Retorica, dove prevale il senso di criterio di ricerca applicato al discorso persuasivo basato su premesse probabili anziché universalmente vere (sillogismo retorico). I l. vengono distinti in comuni (gr. κοινοὶ τόποι, lat. loci communes), ossia generali, indipendenti dall’argomento trattato o dal genere di discorso, e propri, ossia utilizzabili solo in ambiti specifici. Nella tradizione retorica successiva si afferma tuttavia una classificazione più adatta a esigenze di tipo giuridico e scolastico, così come si trova nei Topica di Cicerone e soprattutto nella Institutio oratoria di Quintiliano, ove dalla divisione principale degli argomenti in persone e cose (loci a persona e a re) si procede per altri l. (loci a genere, a natione ecc.; loci a causa, a loco, a tempore, a modo ecc.).

Già in epoca antica il termine l. designava, oltre la formula di ricerca, l’argomento trovato (significativamente Quintiliano adopera come sinonimi i termini locus e argumentum). L’applicazione scolastica dei loci communes alle esercitazioni retoriche condusse presto a una cristallizzazione di certi contenuti ricorrenti, specie in determinate parti dell’orazione. Da qui l’accezione attuale di l. comune.

Matematica

In geometria, una figura è definita l. geometrico dei punti che soddisfano una data proprietà se essa è costituita da tutti e soli i punti che godono di quella proprietà. Per es., una circonferenza è il l. geometrico (o l.) dei punti del suo piano che hanno dal suo centro distanza uguale al raggio; non può dirsi altrettanto per un arco di circonferenza, in quanto esso non è formato da tutti i punti che hanno dal centro distanza pari al raggio.

L. nel piano

fig. 1

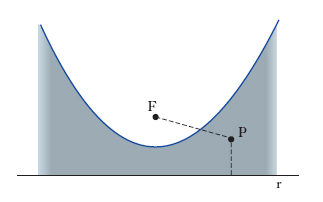
Nel piano, se la condizione data si esprime con una equazione, il l. è di solito costituito da una linea, se invece la condizione si traduce in una disuguaglianza, si ottiene una zona piana: la frontiera di essa separa allora i punti per i quali vale la condizione data dai punti per i quali vale la condizione che si ottiene invertendo la disuguaglianza. Per es., nella fig. 1 è indicato il l. dei punti P per cui |PF|>|Pr|: si tratta dei punti esterni alla parabola di fuoco F e direttrice r.

fig. 2

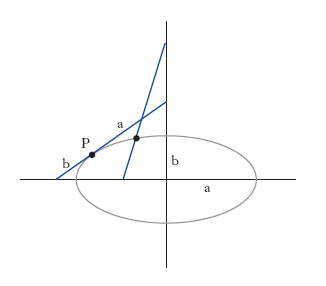
Un l. geometrico può essere dato in diversi modi: a) imponendo direttamente una data condizione, come nel caso già visto della circonferenza; b) sottoponendo una data curva a una determinata trasformazione; per es., una circonferenza può essere trasformata mediante un’omologia, dando luogo a una conica, oppure mediante una trasformazione quadratica, o più in particolare un’inversione, così da ottenere una curva del quart’ordine; c) dando, viceversa, un unico punto P₀ e una totalità ∞¹ di trasformazioni del piano in sé, costituenti un gruppo continuo: per es., se il gruppo è quello delle traslazioni parallele a una retta r, il l. ottenuto è la parallela per P₀ a r, mentre se il gruppo è quello delle rotazioni intorno a un dato punto O, il l. è la circonferenza di centro O e passante per P₀; d) assegnando, infine, una generazione ‘cinematica’ del punto del l., per modo che quest’ultimo possa essere inteso come traiettoria di un punto mobile: così se una sbarretta lunga a + b scorre con i suoi estremi lungo due guide ortogonali (fig. 2), un punto P di essa avente distanze a, b dagli estremi dà origine a un’ellisse di semiassi a, b.

L. nello spazio

Per quanto riguarda i l. nello spazio, se la condizione di appartenenza al l. è espressa da una sola equazione, si ottiene una superficie, mentre una disuguaglianza dà origine a una porzione di spazio limitata da una superficie. Per es., il l. dei punti P equidistanti dai punti A, B è il piano asse del segmento AB, mentre il l. dei punti P tali che |PA|<|PB| è il semispazio che ha come frontiera quel piano e che contiene A (privato, però, del piano stesso). Il l. risulta invece di solito una linea quando la condizione di appartenenza è espressa da due equazioni, ciascuna delle quali rappresenta una superficie passante per la linea. Si noti che nello spazio non solo è possibile considerare l. di punti, ma anche l. di rette, di circonferenze, di curve di un certo tipo, che varino con una data legge: la figura che in questo caso si ottiene è, per lo più, una superficie.

Religione

L. teologici Secondo la definizione protestante, di tipo contenutistico (che si ritrova, per es., nell’opera di Melantone Loci praecipui theologici, 1559), i temi principali e le verità fondamentali della coscienza di fede dei riformatori: per es. la giustificazione, la grazia, il peccato, la fede.

Secondo la definizione cattolica, di tipo formale, le fonti a cui attingere e su cui fondare le affermazioni teologiche, e anche le diverse possibilità di valutazione delle verità di fede. Famoso, al riguardo, il trattato De locis theologicis di M. Cano, pubblicato nel 1563.

Teatro

L. deputati (o mansioni) Costruzioni in legno e tela, simili a capanni aperti sul davanti, che nel dramma liturgico medievale si alzano sul palco (o talamo), separate l’una dall’altra, e che con alcuni elementi architettonici, decorativi o paesaggistici, suggerivano allo spettatore i vari luoghi in cui il fatto si svolgeva. Gli attori, secondo le esigenze dell’azione, passavano dall’una all’altra costruzione, e spesso gruppi di recitanti coesistevano sulla scena, sviluppando più azioni contemporanee. La tecnica perdura nel teatro rinascimentale e ha qualche applicazione in quello più moderno, con scomposizioni della scena in elementi mediante l’illuminazione.