omologia

Conformità o equivalenza tra più parti, termini, elementi.

Biologia

fig. 1

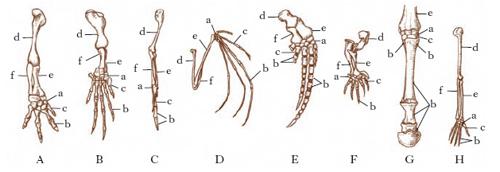
Concetto che esprime il rapporto fra organi o strutture morfologiche propri di categorie tassonomiche diverse (fig. 1), ma aventi la stessa origine embrionale (la mano di un primate e l’ala di un uccello), e in base al quale è possibile individuare le derivazioni filogenetiche di tali categorie tassonomiche da antenati comuni.

Botanica

Comunanza di origine filogenetica di organi anche di aspetto differente, desunta dallo studio comparato e in particolare da quello dello sviluppo degli organi. Si riscontra sia negli organi vegetativi, come fusto, foglia, sia negli apparati riproduttivi quali il fiore e i diversi costituenti di questo. Organi omologhi sono, per es., un cotiledone, una foglia normale, una perula, una spina di cactus, il carpello delle Papilionacee ecc., perché sono tutti organi di origine fogliare.

Geografia

Si chiamano o. alcune corrispondenze di forme nell’andamento perimetrale di continenti o isole o gruppi insulari giacenti ai margini di un dato bacino oceanico: tipiche le o. dell’Atlantico, sia nel bacino settentrionale, sia in quello meridionale: alla sporgenza verso E delle terre canadesi corrisponde una rientranza nell’arcipelago britannico; alla rientranza del Golfo del Messico la sporgenza di NO dell’Africa; alla sporgenza del Brasile la rientranza del Golfo di Guinea. Gran parte di queste o. furono utilizzate da A. Wegener come prova geografica della deriva dei continenti.

Matematica

Geometria proiettiva

fig. 2

fig. 3

fig. 4

O. piana

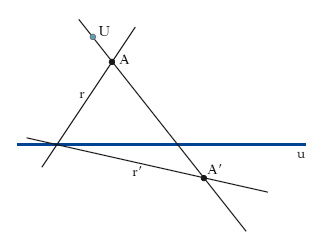
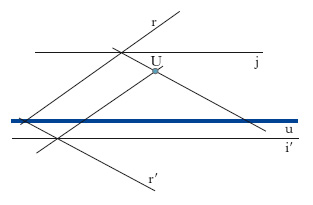
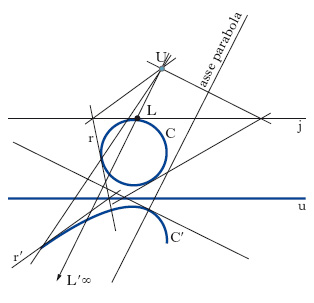
Particolare o. tra due piani coincidenti che ammette una retta u di punti uniti (asse dell’o.) e, dualmente, un punto U (centro dell’o.) centro di un fascio di rette unite. Due punti A, A′ (fig. 2) corrispondenti in un’o. sono allineati con il centro, e così due rette corrispondenti r, r′ si tagliano sull’asse. Un’o. è individuata non appena siano noti centro, asse e due elementi (punti o rette) corrispondenti. In fig. 3 è indicata la costruzione grafica delle due rette limite j, i′ dell’o. cioè delle due rette che corrispondono alla retta all’infinito. In un’o. risultano ovviamente alterate sia le lunghezze di segmenti corrispondenti su r e r′, sia gli angoli tra coppie dirette corrispondenti due a due. Un’o. trasforma le circonferenze in coniche ed è perciò adoperata spesso per tracciare coniche soddisfacenti a date condizioni: in fig. 4 è indicata la costruzione grafica di una parabola C′ a partire da una circonferenza C, che deve essere tangente alla retta limite j (nel punto L).

Le equazioni di un’o. sono del tipo x′−x₀=(x−x₀)/(ax+by+c), y′−y₀=(y−y₀)/(ax+by+c); il centro ha coordinate (x₀, y₀), l’asse ha equazione ax+by+c=1 e l’equazione della retta limite j è ax+by+c=0.

Topologia

La teoria dell’o. costituisce uno dei capitoli centrali della topologia algebrica. Essa si propone di esprimere proprietà geometriche e caratteri topologici di una varietà V_n di dimensione n attraverso n+1 gruppi abeliani, detti appunto gruppi di o. di V_n, ciascuno dei quali si riferisce a un valore della dimensione, da zero fino a n. I gruppi di o. sono invarianti topologici, nel senso che se le varietà V_n e V′_n sono omeomorfe, i rispettivi gruppi di o. sono isomorfi in ciascuna dimensione.

fig. 5

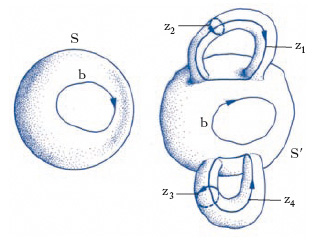
Ci limitiamo a esporre le considerazioni intuitive che riguardano i soli gruppi di o. di dimensione 1 nel caso di una superficie sferica ordinaria S e di una superficie sferica S′ con due manici (fig. 5). Si tratta, in questo caso, di vedere se è possibile tracciare su di esse linee chiuse (cicli) che non le dividano in parti: evidentemente ciò non è possibile per S e pertanto il gruppo di o. H₁(S) si pone uguale a zero. Ben diversamente si comporta S′; si può tracciare su di essa un numero massimo di quattro cicli senza con ciò disconnettere S′: per es., i cicli z₁, z₂, z₃, z₄. Inoltre, definita in modo opportuno la nozione di combinazione lineare a coefficienti interi di cicli, si constata che ogni ciclo che non divida in parti S′ è una combinazione lineare dei cicli indicati: il gruppo di o. unidimensionale di S′ è isomorfo alla somma diretta di quattro copie del gruppo additivo Z degli interi, cioè H₁(S′)∿4Z. Si osservi ora che una linea chiusa che non suddivida una superficie non può essere la frontiera di una parte della superficie: si può allora dire che l’o. della dimensione 1 prende in considerazione i soli cicli che non disconnettono e quindi non sono frontiera di una parte della superficie e trascura invece quelli che sono dei bordi (o cicli contornanti, o cicli circondanti, o cicli omologhi a zero). Generalizzando questa idea s’introducono i gruppi di o. di dimensione p (p minore o uguale alla dimensione n della varietà V); si tratta, questa volta, di esaminare se esistono in V sottospazi di dimensione p che siano privi di frontiera (così come, relativamente alla dimensione 1, è priva di frontiera una linea chiusa) senza però che costituiscano essi stessi la frontiera di una regione (p+1)-dimensionale di V (cioè trascurando sempre i cicli circondanti).

I gruppi di o. si definiscono spesso in maniera del tutto astratta mediante la nozione di complesso di catene; si tratta di una successione di gruppi abeliani liberi: …C₃, C₂, C₁, C₀, C₋₁, C₋₂, C₋₃, … e di omomorfismi … ∂₂, ∂₁, ∂₀, ∂₋₁, ∂₋₂, … ciascuno dei quali agisce come indicato dallo schema seguente:

… C₃ →∂₃ C₂ →∂₂ C₁ →∂₁ C₀ →∂₀ C₋₁∂₋₁→ C₋₂∂₋₂→ …,

con la condizione essenziale che la composizione di due qualunque omomorfismi successivi sia l’omomorfismo nullo. In altre parole, e in generale, l’immagine Im∂_p di ∂_p è contenuta nel nucleo Ker∂_p−1 di ∂_p−1, costituito dagli elementi di C_p−1, ai quali ∂_p−1 fa corrispondere l’elemento nullo di C_p−2. Gli elementi di Im∂_p e di Ker∂_p–1, che ricevono il nome di bordi e, rispettivamente, di cicli di dimensione p, danno luogo ai due gruppi abeliani B_p e Z_p, entrambi contenuti in C_p; l’insieme dei cicli che non sono bordi non costituisce un gruppo, mentre, se si definiscono equivalenti due cicli che differiscono per un bordo, l’insieme delle classi di equivalenza costituisce il gruppo quoziente H_p=Z_p/B_p detto p-mo gruppo di o. del complesso di catene considerato. Il gruppo abeliano H_p può non essere libero; pertanto si decompone nella somma diretta di un gruppo libero R_p e di un gruppo non libero T_p, detti rispettivamente gruppo di Betti e gruppo di torsione, di dimensione p, del complesso di catene considerato; il gruppo R_p è poi isomorfo alla somma diretta di un certo numero r_p di copie del gruppo additivo Z degli interi, mentre T_p si può a sua volta ottenere come somma diretta di gruppi ciclici finiti: gli ordini t₁, t₂, …, t_h di tali gruppi e l’intero r_p si chiamano coefficienti di torsione e, rispettivamente, numero di Betti p-dimensionale del complesso di catene considerato.

La teoria dell’o. possiede varie diramazioni, tutte in continuo sviluppo. Alcune di esse hanno carattere spiccatamente algebrico e studiano l’o. come esempio notevole di funtore che agisce tra le categorie dei complessi simpliciali e degli spazi topologici da un lato e quella dei gruppi abeliani dall’altro. Altre teorie hanno invece un carattere più nettamente topologico, cioè geometrico. Profondi legami intercorrono tra la teoria dell’o. e quella dell’omotopia: in molti casi la determinazione dei gruppi di o. serve di aiuto per ottenere i gruppi di omotopia e quindi per avviare a soluzione i problemi, di svariatissimo tipo, che si possono ricondurre alla nozione di omotopia.

Algebra omologica

Importante ramo dell’algebra che, sorto allo scopo di fornire strumenti adatti allo studio dei problemi di algebra che si incontrano nella topologia (per es., nella teoria dell’o., dalla quale ha preso il nome) si è poi ampiamente sviluppato con H. Cartan, S. Eilenberg, J. Léray, G. Hochschild, J.-L. Koszul e altri, anche come disciplina autonoma. Fu lo studio di certi spazi topologici (W. Hurewicz, 1935) a porre la questione di esprimere la dipendenza dei loro gruppi d’o. dal loro gruppo fondamentale, e le ricerche in questa direzione diedero l’impulso allo studio della (co)omologia dei gruppi astratti. Questa teoria ha trovato successive notevoli applicazioni ai gruppi finiti, alla teoria dei corpi di classi e varie connessioni con la K-teoria e la caratterizzazione dei gruppi liberi. Ma i metodi della topologia algebrica hanno portato anche alla costruzione di teorie di (co)omologia per algebre associative e algebre di Lie. Tuttavia ancora un problema topologico, tradotto in termini puramente algebrici, ha condotto al fondamentale concetto di funtori derivati ottenuti mediante la nuova operazione di prodotto torsione, derivata dal prodotto tensoriale con un procedimento iterabile. Il rapido sviluppo della teoria delle categorie e dei funtori ha interagito con lo sviluppo dell’algebra omologica, influenzandone decisivamente i modelli e i metodi; cosicché vari argomenti di algebra omologica hanno trovato sistematiche trattazioni.

Dalla topologia algebrica proviene l’altro concetto fondamentale di sequenza spettrale, che può esser definita in una categoria abeliana come una sequenza di oggetti differenziali. Mediante opportune definizioni si possono costruire limiti e convergenza di sequenze spettrali in una categoria abeliana, che permettono di ottenere per approssimazioni successive l’o. di un dato oggetto.

Zoologia

In etologia, i tipi di comportamento, come gli organi, si possono omologare e dedurre da forme originarie comuni. Sono omologhi quegli elementi del comportamento che possiedono lo stesso tipo neuromuscolare. In quanto forme temporali, i tipi di comportamento sono tanto più sicuramente omologhi quanto più numerosi sono i caratteri particolari che essi hanno in comune e quanto più si corrispondono nel succedersi delle azioni.