omotopia
In matematica, la corrispondenza generata tra due catene di un complesso, e più in generale tra due applicazioni, quando la prima può deformarsi con continuità nella seconda.
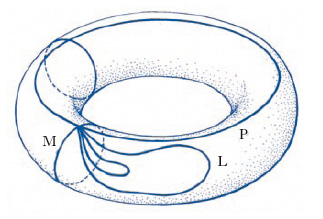
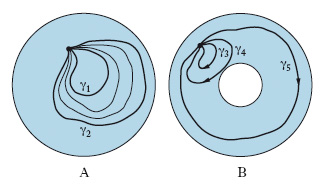
La teoria dell’o. costituisce uno dei capitoli della topologia algebrica più importanti e ricchi di applicazioni. La nozione intuitiva di o. si basa sulle deformazioni di un ciclo (linea chiusa) orientato, tracciato su una superficie, che avvengano senza che si perda il carattere di ciclo. Un ciclo che si possa deformare fino a ridursi a un punto si dice omotopo a zero; nel caso della superficie del toro, per es., ciò è possibile per la linea L in fig. 1, ma non è possibile né per un meridiano M, né per un parallelo P. Un problema più generale consiste poi nel considerare sulla superficie in esame due cicli basati nello stesso punto, anziché uno solo, e nel vedere se è possibile variare in modo continuo uno dei due fino a farlo coincidere con l’altro. Ora, se la superficie è un cerchio, la cosa è sempre possibile: in fig. 2A sono appunto indicati alcuni stadi della deformazione che conduce dal ciclo γ1 al ciclo γ2; invece, se la superficie è, per es., una corona circolare (fig. 2B), alcune volte la deformazione è ancora possibile, ma altre volte no, perché ostacolata dal foro della corona: così, è possibile da γ3 a γ4, ma non da γ3 a γ5.
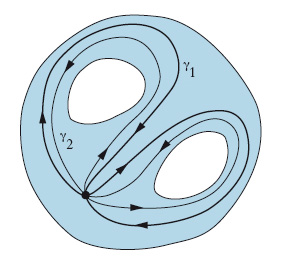
Ciò si esprime brevemente dicendo che due cicli qualsiasi appartenenti al cerchio sono sempre collegati da una o. (che è, appunto, la deformazione che fa passare dall’uno all’altro), o anche che sono omotopi, mentre due cicli della corona circolare possono essere omotopi (come γ3 e γ4) o anche non omotopi (come γ3 e γ5). Con maggiore esattezza, più che di cicli omotopi si dovrebbe parlare di applicazioni omotope poiché l’o. è una relazione non tanto tra cicli quanto tra due applicazioni; tuttavia è più intuitivo riferirsi senz’altro ai cicli, cioè, sostanzialmente, alle immagini delle applicazioni. Tornando al caso della corona circolare, s’intuisce che due cicli sono omotopi soltanto se compiono uno stesso numero n di giri, nello stesso verso, attorno al foro della corona. Se, allora, si suddividono i cicli in classi di equivalenza ponendo in una medesima classe tutti i cicli tra loro omotopi, si ottiene, nel caso del cerchio (i cui cicli sono anzi tutti omotopi a zero) un’unica classe; nel caso della corona, invece, si ha una classe per ogni valore di n. L’insieme di tali classi, che ha la struttura algebrica di un gruppo, si chiama gruppo di o. 1-dimensionale, o anche gruppo fondamentale, della superficie considerata, e si indica con il simbolo π1: si ha dunque π1(A)=0, π1(B)=Z (A, B, Z sono rispettivamente il cerchio, la corona e il gruppo additivo dei numeri interi relativi). Dagli esempi indicati s’intuisce che il gruppo fondamentale di una superficie dà un’idea della presenza e del numero dei ‘fori’ della superficie, intendendo genericamente per foro ogni ostacolo che impedisca a certe linee chiuse di potersi ridurre, attraverso una deformazione continua, a un unico punto. In modo del tutto analogo si introduce il gruppo fondamentale di uno spazio topologico T. Esso non è, per solito, commutativo; ciò si vede facilmente esaminando, per es., la superficie con due fori della fig. 3: i due cicli γ1 e γ2 non sono infatti omotopi perché non è possibile passare, mediante una deformazione continua, dal primo al secondo.
Si considerano, più in generale, gruppi di o. di dimensione qualunque n>1 di uno spazio topologico T. A differenza del gruppo fondamentale, essi sono sempre commutativi: si indicano con il simbolo πn(T) e si definiscono a partire dalle applicazioni di una superficie sferica n-dimensionale verso lo spazio T.