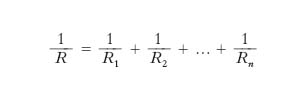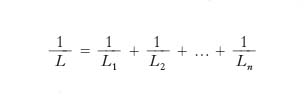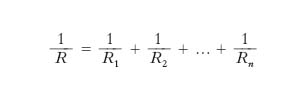parallelo

In una qualunque superficie generata dalla rotazione di una curva intorno a un asse fisso e a essa rigidamente collegato (superficie di rotazione), il cerchio descritto da un punto della curva generatrice, cioè il cerchio sezione della superficie con un piano perpendicolare all’asse.

In geometria, l’aggettivo p. si riferisce a rette complanari, o di piani, non aventi alcun punto comune, o a due curve, superfici ecc., che conservano distanza costante in ogni loro punto. Per estensione il termine si applica a tutto ciò che si estende e procede nella stessa direzione di un altro ente, mantenendo rispetto a questo sempre la stessa distanza.

Fisica

In ottica, si dicono p. due polarizzazioni, in particolare due nicol, coassiali, disposte in modo che le sezioni principali siano p. tra loro: pertanto un raggio polarizzato emergente dal primo emerge dal secondo nelle stesse condizioni di polarizzazione.

Geografia

Sulla superficie della Terra, p. geografici (o circoli p., o più spesso paralleli) sono le linee ideali secondo le quali essa è tagliata dai piani perpendicolari all’asse terrestre e quindi paralleli fra loro; convenzionalmente i p. sono associati alle corrispondenti latitudini nord e sud; i p. corrispondenti a 90° si riducono a 2 punti, che sono i poli geografici.

Sulla sfera celeste, p. celesti sono i circoli descritti apparentemente dagli astri per effetto della rotazione diurna (apparente) della sfera celeste, causata dalla rotazione reale della Terra intorno al proprio asse. I p. celesti sono perpendicolari all’asse del mondo e hanno i centri su di esso.

Informatica

Calcolo p. Procedure e algoritmi concepiti in modo da generare famiglie di operazioni indipendenti da eseguire simultaneamente con processori anche distinti.

Un elaboratore p. è quello su cui si possono effettuare operazioni diverse simultaneamente. Una porta p. è una porta degli elaboratori, utilizzata per connettere periferiche (➔ periferico) agli stessi; tipicamente è usata per connettere una stampante.

Matematica

Il significato di p. è connesso alla definizione di Euclide di rette p. in un piano, secondo la quale due rette si dicono p. se due loro segmenti, prolungati, non s’incontrano mai. La definizione trascura però la questione dell’esistenza di rette p., questione connessa con il postulato dell’infinità della retta e con la critica del 5° postulato di Euclide. Accanto a quella definizione si può assumere quest’altra: si chiama p. a una retta data il luogo dei punti del piano (che si postula essere una retta) aventi una data distanza da essa e giacenti da una banda rispetto a essa. La definizione si estende analogamente a due piani dello spazio, ovvero a una retta e un piano; in quest’ultimo caso la condizione necessaria e sufficiente per il parallelismo è che esista una retta nel piano p. alla retta data, ovvero che esista un piano per la retta p. al piano dato. Per indicare che due rette r, s sono p., si usa scrivere r∥s (si legge: r è p. a s); analogamente tra due piani o tra retta e piano.

La nozione di enti p. si generalizza in vari modi. In un iperspazio euclideo, o affine, due spazi subordinati, delle dimensioni h, k, si dicono p. se non hanno punti comuni e se il loro spazio congiungente ha dimensione non superiore ad h+k; in caso contrario i due spazi si dicono sghembi. Due spazi coincidenti (o, più in generale, due spazi uno dei quali sia contenuto nell’altro) si considerano anch’essi paralleli. Quando si introducano gli elementi impropri, la relazione di parallelismo tra due rette (distinte) si può esprimere dicendo che esse hanno in comune un punto improprio; due piani p. hanno in comune la retta impropria; in genere due spazi subordinati p. e tali che nessuno dei due sia contenuto nell’altro, hanno in comune esclusivamente punti impropri.

Postulato delle p. È detto anche 5° postulato di Euclide, perché enunciato come quinto nei suoi Elementi: per un punto esterno a una retta è possibile condurre una e una sola retta parallela alla retta data. Equivalentemente: se in un piano due rette sono tagliate da una terza in modo che angoli coniugati interni non siano supplementari, esse si intersecano da quella parte ove la somma di tali angoli è inferiore a due retti.

Questione delle p. È sorta dal problema di stabilire se fosse possibile o no dedurre (cioè dimostrare) il postulato delle parallele partendo dagli altri postulati della geometria elementare piana. La questione fu completamente risolta, nel senso che fu dimostrata l’indipendenza del 5° postulato, e quindi la possibilità di geometrie in cui esso non vale, da K.F. Gauss, N.I. Lobačevskij, J. Bolyai, B. Riemann (➔ geometria).

Condizioni di parallelismo Sono relazioni, analitiche o grafiche, cui devono soddisfare le rappresentazioni di due rette, o di due piani ecc., affinché le rette, i piani ecc., siano fra di loro paralleli. Così per es., nel piano cartesiano, o affine, la condizione di parallelismo di due rette ax+by+c = 0, a′x+b′y+c′=0 è che sia ab′−a′b=0; nello spazio, la condizione di parallelismo dei due piani ax+by+cz+d = 0, a′x+b′y+c′z+d′=0 è ab′−a′b=ac′−a′c=bc′–b′c=0 e la condizione di parallelismo del piano ax+by+cz+d=0 e di una retta avente parametri direttori l, m, n è al+bm+cn=0. Per due vettori la condizione di parallelismo si può esprimere con l’annullarsi del loro prodotto vettoriale.

Tecnica

fig. 1

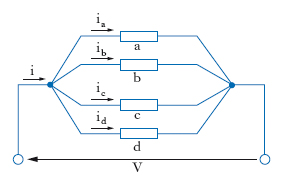
In elettrotecnica collegamento in p., collegamento di più bipoli (condensatori, resistori, generatori ecc.), detto anche accoppiamento in p. o in derivazione, ottenuto riunendo insieme le estremità corrispondenti dei vari elementi, che in questo modo risultano sottoposti alla medesima tensione elettrica. Se gli elementi messi in p. sono polarizzati (è il caso, per es., delle pile, dei condensatori elettrolitici ecc.), il collegamento deve essere fatto tenendo conto della loro polarità, e precisamente in modo che risultino connessi insieme i poli omonimi. Per l’accoppiamento in p. di più alternatori, per es., occorre che le tensioni abbiano la stessa frequenza, la stessa ampiezza, e che siano in concordanza di fase nell’istante in cui si fanno le connessioni; inoltre, nel caso di alternatori trifase occorre che le sequenze delle terne delle tensioni siano le stesse. Applicando una tensione continua V a un gruppo di 4 generici elementi a, b, c, d connessi in p. (fig. 1), l’intensità i della corrente è la somma delle correnti ia, ib, ic, id che percorrono ogni elemento: l’intero gruppo si comporta cioè come un unico elemento la cui conduttanza è la somma delle conduttanze dei singoli elementi. Analogamente, per correnti alternate l’ammettenza complessiva di più elementi in p. è la somma delle loro ammettenze. Poiché l’ammettenza è l’inverso dell’impedenza, dette Z1, Z2, ..., Zn le impedenze dei singoli elementi, Z l’impedenza complessiva, si ha:

[1] formula.

Se, in particolare, le impedenze degli elementi sono tutte uguali fra loro, l’impedenza complessiva si riduce a 1/n dell’impedenza di un solo elemento. Dalla [1] derivano le relazioni valide nel caso di collegamento in p. di più elementi passivi omogenei (resistori, induttori, condensatori ecc.). Infatti, dette C₁, C₂, ..., C_n le capacità dei singoli condensatori, dalla [1] si ricava per la capacità complessiva C il valore

C = C₁ + C₂ + … + C_n.

Invece, nel collegamento in p. di più resistori l’impedenza Z si riduce alla resistenza R e la [1] diviene

Infine, nel collegamento in p. di più induttori, dette L₁, L₂, ..., L_n le induttanze dei singoli induttori, dalla [1] si ottiene

,

essendo L l’induttanza complessiva.

fig. 2A

In generale, si ha il collegamento in p. di due circuiti (per es., bifilari) quando i fili a e b dell’uno sono collegati ai fili a e b dell’altro a una delle estremità dei circuiti (fig. 2A) o a entrambe (fig. 2B), per cui i due circuiti risultano simultaneamente interessati al trasferimento di una parte dell’energia che prima o al di là del punto in cui è effettuato il p. viene trasmessa su un solo circuito c. Nelle reti di distribuzione telefoniche in cavo, due distributori sono tra loro in p. quando le stesse coppie di distribuzione sono collegate all’uno e all’altro e possono quindi essere utilizzate indifferentemente nell’uno o nell’altro punto di distribuzione; il che si ottiene giuntando ordinatamente tra loro, nel giunto di diramazione dei cavi diretti ai due distributori, i fili delle coppie che fanno capo ai distributori stessi.

Si chiama p.-serie quel tipo di collegamento di più bipoli, costituito da più gruppi di bipoli in p. tra loro, tali gruppi essendo collegati in serie.