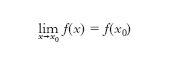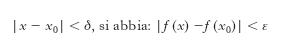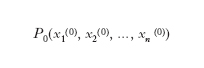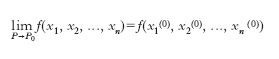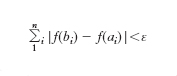continuità

Biologia

C. del plasma germinale

Teoria biologica di M. Nussbaum e A. Weismann, secondo la quale il ‘plasma germinale’, portatore dei caratteri ereditari, contenuto nelle cellule germinali o gameti, non si distribuirebbe a tutte le cellule del corpo dell’organismo che si sviluppa dall’uovo fecondato, ma verrebbe fin dall’inizio limitato a una determinata linea di discendenza cellulare, che nell’adulto formerebbe poi i gameti. La teoria ha trovato molte conferme in varie osservazioni embriologiche.

Fisica

Si parla generalmente di fenomeni e di corpi o sistemi continui, di c. delle leggi naturali, benché la realtà naturale abbia una struttura prevalentemente discontinua. Ciò accade perché il potere risolutivo dei nostri sensi e della maggior parte dei nostri strumenti non è tale da rivelare tale discontinuità. Così, specialmente nella tecnica (teoria dell’elasticità, meccanica applicata ecc.), di solito è lecito e conveniente considerare i corpi come continui.

Per l'equazione di continuità ➔ continuità, equazióne di.

Per la meccanica dei sistemi continui ➔ meccanica.

Matematica

Il concetto di c. si può definire attraverso la considerazione e l’analisi delle seguenti proprietà: a) divisibilità all’infinito; b) esistenza di un elemento intermedio tra due elementi quanto si vogliano vicini; c) gradualità nel passaggio da uno stato a un altro (per giungere dallo stato iniziale a quello finale bisogna passare per tutti gli stati intermedi, attraverso variazioni insensibili); d) assenza di ‘salti’ o di ‘lacune’.

C. degli enti geometrici

Lo spazio della geometria elementare deve essere concepito come continuo. Il punto della geometria deve essere infatti concepito come privo di estensione, deve cioè essere ammessa la divisibilità all’infinito, in parti sempre più piccole, di linee, superfici, solidi. Ciò è stato chiarito sin dall’antichità greca, soprattutto attraverso la disputa tra Pitagorici ed Eleati. I Pitagorici concepivano il punto geometrico come una monade, un indivisibile, estremamente piccolo ma non privo di estensione. Tale ipotesi si dimostrò incompatibile con l’esistenza di grandezze geometriche tra di loro incommensurabili, e portava a conseguenze assurde. I famosi paradossi di Zenone di Elea sembra siano appunto una riduzione all’assurdo dell’ipotesi pitagorica della discontinuità dello spazio geometrico.

Analisi del concetto intuitivo di continuità

Nella seconda metà dell’Ottocento è stata data una definizione rigorosa della c. degli enti della geometria elementare. Si è visto che, per es., l’intuizione della c. della retta può essere tradotta in un postulato della c. della retta, al quale possono essere date diverse forme e che nella forma di Dedekind (1872) si esprime così: se i punti di un segmento sono distribuiti in due classi (non vuote) H e K, in modo che ogni punto appartenga o ad H o a K e che ogni punto della classe H preceda tutti i punti della classe K (in uno dei due ordini che si possono fissare sulla retta), allora esiste un punto di separazione, tale che tutti i punti che lo precedono appartengono alla classe H, tutti quelli che lo seguono alla classe K. Si tratta di un nuovo postulato, e non di un teorema, in quanto la proposizione esposta non può essere dedotta dai precedenti postulati dell’appartenenza e dell’ordine. Il postulato della c. precisa l’intuizione della c. come assenza di ‘salti’, di ‘lacune’ (➔ sezione).

Le funzioni continue

Una funzione per la quale si ha:

è detta funzione continua in un punto x₀ del suo intervallo di definizione. Ciò vuol dire che a una ‘piccola’ variazione della x corrisponde una ‘piccola’ variazione della funzione ovvero che, fissato un numero ε positivo piccolo a piacere, a esso corrisponde un numero δ>0 tale che, per ogni x soddisfacente la limitazione

Una funzione f (x) che sia continua in ogni punto di un intervallo si dice continua in quell’intervallo. Più in generale si dice continua in un punto

che sia di accumulazione per il suo campo di definizione e vi appartenga, una funzione f (x₁, x₂,.., x_n) tale che

Le più importanti funzioni continue

Il concetto di c. ammette forme, per così dire, più forti (funzione uniformemente continua, funzione assolutamente continua) e forme più deboli (funzione quasi continua, funzione semicontinua ecc.). Funzione assolutamente continua Funzione f(x) è tale nel suo intervallo di definizione (a, b) quando in corrispondenza ad ogni ε>0 è possibile determinare un δ>0 tale che, se (a1, b1), (a2, b2),..., (an, bn) è un qualunque insieme finito di intervalli contenuti in (a, b), privi a due a due di punti comuni, e la cui somma delle lunghezze sia ⟨δ, risulti

Ogni funzione assolutamente continua è anche continua.

Funzioni equiuniformemente continue

Più funzioni f (P) (formanti una famiglia qualunque), definite in un insieme A sono equiuniformemente continue se per ogni ε>0 esiste un δ>0, dipendente solo da ε, in modo che per ogni f (P) della famiglia e per ogni coppia P₁, P₂ di punti di A tali che sia ‾‾‾‾‾P₁P₂⟨δ risulti |f (P₁)−f (P₂)|⟨ ε. c).

Funzione quasi continua

Funzione continua nel suo insieme di definizione C, a esclusione di un insieme di misura nulla; in altre parole, comunque si prefissi un numero ε>0 è possibile determinare un insieme C_ε, di misura minore di ε, contenuto nell’insieme di definizione C della funzione, in modo che nell’insieme C−C_ε la funzione risulti continua. La nozione di funzione quasi continua è talmente generale che abbraccia tutte le funzioni conosciute.

Funzione semicontinua

Una funzione (il concetto generalizza quello di funzione continua) y = f (x) si dice semicontinua inferiormen;te nel punto x₀ se, assegnato comunque un numero positivo ε, è possibile determinare un numero positivo δ tale che per ogni x soddisfacente alla limitazione |x −x₀|⟨δ si abbia f(x)>f (x₀)−ε. Analogamente per la semicontinuità superiore. Se una funzione è semicontinua inferiormente e superiormente in x₀, è anche continua in x₀.

Funzione uniformemente continua

Una funzione y = f (P) è uniformemente continua se comunque si prefissi un ε>0 è possibile determinare un δ>0, dipendente soltanto da ε, in modo che non appena due punti P₁, P₂ del campo di definizione abbiano distanza minore di δ, risulti |f(P₁) −f(P₂)|⟨ ε. Vale il teorema di Heine: una funzione continua in un insieme chiuso e limitato è ivi uniformemente continua.

Applicazione continua

In topologia, l’applicazione continua di uno spazio topologico A in un altro A′, è una applicazione che fa corrispondere a punti ‘vicini’ di A punti ‘vicini’ di A′: più esattamente, se al punto P di A corrisponde il punto P′, di A′, allora, fissato un intorno qualsiasi I′ di P′, esiste un intorno I di P che viene trasformato in un insieme di A′ tutto contenuto in I′. La nozione di applicazione continua, previa particolarizzazione degli spazi A, A′, comprende, in particolare, la nozione di funzione continua.

Tecnica

Gruppi di continuità

fig

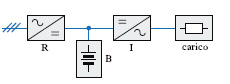
Alimentatori capaci di continuare a fornire energia elettrica, senza apprezzabile interruzione, anche in caso di mancanza di fornitura da parte della rete. Nel caso in cui non sia tollerabile ammettere interruzioni nemmeno di frazioni di secondo, si parla di c. assoluta. Questo è necessario, per es., nel caso dell’alimentazione degli elaboratori elettronici, per i quali un’interruzione significa la perdita di programmi e di dati, con necessità di riavvio di tutto il sistema e spesso con danni assai gravi; particolare importanza ha poi il caso in cui l’elaboratore presiede a sistemi di sicurezza e di intervento sia nel settore militare, sia in quello civile. Nel passato si utilizzavano dei gruppi di c. rotanti, costituiti generalmente da un gruppo motogeneratore provvisto di volano. Con lo sviluppo dei convertitori statici si sono affermati i cosiddetti gruppi statici di c. (UPS, uninterruptible power supply), costituiti essenzialmente da un raddrizzatore controllato, da un invertitore e da una batteria inserita in parallelo all’uscita del raddrizzatore (v. .). Il carico, per il quale deve essere assicurata la c. di funzionamento, è alimentato dall’invertitore I che fornisce una tensione alternata stabile nel tempo. Nel funzionamento normale la batteria B si trova sotto carica di mantenimento e l’invertitore è alimentato dal raddrizzatore R, collegato a sua volta alla rete elettrica. In caso di guasto nella rete e improvvisa mancanza di tensione, l’invertitore è alimentato dalla batteria e può continuare a fornire potenza al carico, il quale non risente del disturbo in rete.