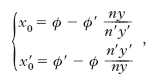sistema
sistema Nell’ambito scientifico, qualsiasi oggetto di studio che, pur essendo costituito da diversi elementi reciprocamente interconnessi e interagenti tra loro e con l’ambiente esterno, reagisce o evolve come un tutto, con proprie leggi generali.
Insieme di enti astratti o concettuali strettamente coordinati, anche se non necessariamente dipendenti uno dall’altro.
Anatomia
Complesso di strutture e di organi che hanno in comune una funzione specifica. Il termine, spesso usato come sinonimo di apparato, designa altre volte, in modo insostituibile, strutture che, pur avendo in comune determinate attività funzionali, sono prive di continuità (per es., s. reticolo-istiocitario). Il s. respiratorio è composto dalle cavità nasali, dal naso-faringe, laringe-trachea, polmoni; il s. digerente comprende bocca, faringe, esofago, stomaco, intestino e ghiandole annesse (fegato, pancreas ecc.); al s. circolatorio appartengono il cuore, le arterie, i capillari, le vene; il s. nervoso è diviso in centrale (composto dall’encefalo e dal midollo spinale), periferico (comprendente i nervi periferici cranici e spinali) e neurovegetativo. Nell’ambito del s. nervoso centrale, vengono indicati col nome di s. particolari complessi funzionali, quali il s. piramidale (➔ piramide) e il s. extrapiramidale (➔ extrapiramidale, sistema).
Botanica
S. sessuale
Metodo di classificazione delle piante, proposto da C. Linneo nel 1735, basato sui caratteri degli organi riproduttivi (impropriamente detti sessuali), cioè stami e pistilli. Basandosi sul numero degli stami e/o dei carpelli presenti in un fiore, sulla loro concrescenza o meno e su altri caratteri analoghi, Linneo distribuì le piante in 24 classi, di cui 23 per le Fanerogame e una sola per le Crittogame. Ognuna delle 23 classi di Fanerogame era suddivisa in gruppi, designati da Linneo come ‘ordini’, fondati sul numero degli stili, corrispondenti ai carpelli, o per il numero degli stami (per es., per le classi Mono-, Di- e Poliadelfia). Il s. sessuale si rivelò molto pratico per giungere alla rapida determinazione dei generi e fu usato per circa un secolo. Spesso però rivela il suo carattere artificiale, di cui lo stesso Linneo era conscio, per es., quando piante di evidente affinità sono allontanate e distribuite in due o più classi (per es., le Lamiacee erano collocate in parte nella Diandria, in parte nella Tetrandria, avendo alcune 2 stami e altre 4, mentre il fico era compreso fra le Crittogame non avendo esternamente fiori manifesti).
Diritto
S. di pagamento
Strumenti e procedure diretti a ridurre gli spostamenti materiali di denaro da un soggetto a un altro al fine di regolare le transazioni economiche instaurate. Ciò si realizza attraverso il ricorso alla moneta bancaria, con la quale si può adempiere a una obbligazione pecuniaria in luogo dell’utilizzo della moneta legale. I s. di pagamento impongono l’instaurazione di un rapporto da parte di chi intende avvalersene con i soggetti autorizzati a emetterli: sono tali gli istituti bancari, gli intermediari finanziari in possesso dei requisiti indicati dalla legge e dall’autorità di vigilanza, e le poste. Rientrano tra i s. di pagamento gli assegni bancari, circolari e postali, le carte di credito e di debito, i bonifici bancari, i vaglia postali ecc. L’evoluzione in campo tecnologico ha consentito, inoltre, la diffusione di s. di pagamento telematici (per es., le carte prepagate) che si avvalgono della moneta elettronica o dell’apertura di conto per effettuare gli acquisti in rete. Rilevanza assume anche l’istituto della compensazione quale mezzo di estinzione delle obbligazioni alternativo all’adempimento.
Chimica
Per il sistema periodico ➔ elemento.
Economia
S. economico
L’organizzazione di un’economia, riferita a uno o più paesi o all’economia internazionale in generale: così, per es., si parla di s. economico nazionale, internazionale, regionale, comunitario ecc., in riferimento ai singoli aspetti dell’economia presi in considerazione o all’economia nel suo complesso. Il s. economico è quindi costituito dall’insieme generale di istituzioni economiche, sociali, politiche ma, anche, da beni, enti, individui, leggi in vigore ecc., posti in rapporto tra loro. Si parla di s. economico stabile quando vi è stabilità (assenza di crisi) di consumi, investimenti e produzione. S. bancario o creditizio L’insieme degli istituti di credito operanti in uno Stato, visti nella loro articolazione funzionale e nei loro rapporti di concorrenza e di gerarchia.
S. monetario internazionale
Definizione
Insieme di regole e norme, definite dai trattati internazionali e integrate da convenzioni e usi accettati dai paesi che ne fanno parte, riguardanti: i rapporti di cambio tra le monete dei diversi paesi (regime dei cambi); le modalità e i criteri di regolamento dei pagamenti internazionali (regime valutario); le caratteristiche degli strumenti universalmente accettati come mezzi di pagamento e utilizzati come moneta di riserva (regime di riserva); le modalità di correzione degli squilibri della bilancia dei pagamenti; gli aiuti finanziari tra banche centrali o Stati nel caso di crisi della bilancia dei pagamenti.
La necessità di stabilire in forma più o meno codificata l’insieme delle norme che regolano i rapporti economici tra paesi è una conseguenza dell’esistenza di una pluralità di monete (la cui emissione è gestita dalle singole banche centrali) che richiede dei criteri che regolino la loro convertibilità. Tali regole sorgono però in precisi momenti storici, generalmente sotto l’impulso dei paesi economicamente e politicamente ‘dominanti’ come, per es., la Gran Bretagna nel periodo del gold standard (➔), e gli Stati Uniti nel secondo dopoguerra. Come conseguenza, i s. monetari internazionali sono generalmente ‘asimmetrici’, nel senso che il paese che assume il ruolo guida (paese leader) ha il vantaggio di trasferire sugli altri l’onere dell’aggiustamento della bilancia dei pagamenti e di far accettare la propria moneta cartacea anche al resto del mondo a saldo degli scambi commerciali e finanziari (il cosiddetto signoraggio).
Fasi principali dell’evoluzione dei s. monetari internazionali. Tra la fine delle guerre napoleoniche e il 1914 il s. monetario internazionale si mosse gradualmente verso un regime di gold standard che fu realizzato pienamente intorno al 1880. Sotto la leadership della Gran Bretagna la sterlina operò come moneta internazionale consentendo un buon funzionamento del meccanismo dei pagamenti internazionali. Tale s. fu però caratterizzato da forti fluttuazioni dell’occupazione e dei prezzi. Dopo la Prima guerra mondiale furono fatti dei tentativi per ripristinare la convertibilità dell’oro, anche se su base limitata, ma furono abbandonati con il sopraggiungere della grande depressione degli anni 1930, cui seguì un periodo caratterizzato dalla fluttuazione dei tassi di cambio, da svalutazioni competitive e dal crescente ricorso alle restrizioni commerciali come strumento per sostenere l’occupazione interna dei singoli paesi.
Al termine della Seconda guerra mondiale, con gli accordi di Bretton Woods (➔ FMI) fu ripristinato il multilateralismo dei pagamenti e istituito un sistema di cambi fissi ma aggiustabili con il supporto di vari organismi sovranazionali (Fondo monetario internazionale, Banca internazionale per la ricostruzione e lo sviluppo). La valuta chiave del sistema di Bretton Woods divenne il dollaro, cioè la moneta del principale paese vincitore della Seconda guerra mondiale, che costituì la più importante attività di riserva detenuta dalle banche centrali. Tale sistema terminò di fatto nel 1971 con la dichiarazione di inconvertibilità del dollaro decisa unilateralmente dal presidente R. Nixon.
A esso ha fatto seguito il passaggio a un regime di cambi fluttuanti caratterizzato dalla fine del ruolo monetario dell’oro e dalla coesistenza di una pluralità di valute convertibili. Il dollaro mantiene ancora il ruolo di valuta di regolamento dei pagamenti internazionali e di intervento sul mercato dei cambi da parte dei governi, ma nel tempo hanno assunto un peso più consistente l’euro e lo yen giapponese. Nel s. successivo a quello di Bretton Woods, la moneta internazionale risulta quindi composta da più monete nazionali detenute nei portafogli degli operatori privati e nelle riserve valutarie delle banche centrali in proporzioni variabili a seconda dell’andamento dei tassi di cambio. Grazie al regime dei cambi fluttuanti, le banche centrali possono recuperare gradi di libertà per la gestione monetaria finalizzata a obiettivi di stabilità interna. Anzi, secondo alcune correnti accademiche, tra le quali assume particolare rilievo il monetarismo di M. Friedman, un regime di completa fluttuazione dei cambi solleverebbe le autorità monetarie nazionali dalla responsabilità della gestione delle riserve valutarie. Il mercato, infatti, provvederebbe ad aggiustare il livello dei cambi, portandolo a un livello compatibile con l’equilibrio dei conti con l’estero. In questa impostazione teorica sono escluse regole specifiche di coordinamento internazionale delle politiche economiche, dato che la stabilità monetaria internazionale è assicurata dallo sforzo realizzato da ciascun paese nel garantire le condizioni di controllo monetario e di equilibrio del bilancio statale interno e nel non ostacolare il libero svolgimento delle forze di mercato.
Nella realtà il s. monetario internazionale che ha fatto seguito a quello di Bretton Woods è stato posto di fronte a problemi strutturali di notevole rilievo che hanno completamente smentito la possibilità di realizzazione di un sistema efficiente in base ai suddetti criteri. In particolare i due shock petroliferi del 1973-74 e del 1979-80, il mix di politiche monetarie e fiscali adottate dall’amministrazione del presidente R. Reagan nella prima metà degli anni 1980, e la crisi del debito dei paesi in via di sviluppo portarono a considerevoli disavanzi delle partite correnti di numerosi paesi, e in particolare del paese a valuta di riserva (per quasi tutti gli anni 1980 e ancora nel 1994 gli Stati Uniti avevano disavanzi correnti enormi, in media superiori al 3% del PIL dal 1986 al 1988). Inoltre, gli sviluppi senza precedenti dell’attività di intermediazione bancaria internazionale, avviatasi negli anni 1970 con la nascita dei mercati delle eurovalute, nonché la maggiore possibilità di diversificazione (per scadenza, rendimento e valuta) delle attività finanziarie internazionali offerta da tali sviluppi, hanno aumentato enormemente la sostituibilità tra le monete ma hanno accresciuto anche l’instabilità dei tassi dei cambi e favorito l’emergere di fenomeni speculativi di carattere destabilizzante, che possono avere effetti indesiderati sui tassi di cambio. A questi flussi speculativi si associa la tendenza mostrata dai cambi determinati sul mercato ad allontanarsi dai valori di equilibrio con conseguenze assai rilevanti sui rapporti di competitività tra paesi e sull’introduzione di nuove forme di protezionismo nei rapporti commerciali internazionali.
Venuti meno gli accordi di Bretton Woods, vari tentativi e proposte di riportare un certo ordine nel sistema dei cambi si sono susseguiti, ma senza dar luogo ad assetti stabili e duraturi, se non con l’eccezione del Sistema Monetario Europeo (➔ SME). In ogni caso, l’esigenza avvertita dai principali paesi industrializzati (il cosiddetto gruppo dei sette composto da Stati Uniti, Giappone, Germania, Gran Bretagna, Francia, Italia e Canada) di stabilizzare i cambi attraverso un più stretto coordinamento delle politiche economiche ha compiuto alcuni importanti passi con i cosiddetti accordi del Plaza (1985) e del Louvre (1987), anche se a essi non ha fatto seguito una definizione di impegni più continuativi e decisi volti alla creazione di un s. monetario internazionale basato su cambi più stabili. Oltre ai pericoli protezionistici derivanti dalla eccessiva oscillazione dei cambi, vi è poi il problema del debito estero di numerosi paesi in via di sviluppo, che incrina la stabilità del sistema bancario internazionale e rallenta lo sviluppo economico mondiale per effetto delle politiche restrittive che i paesi indebitati sono costretti a seguire. Nonostante le politiche di stabilizzazione dei paesi indebitati, in genere concordate con il Fondo monetario internazionale, e i piani di ristrutturazione del debito (come il piano Baker del 1985 e il piano Brady del 1989), il problema è rimasto tuttora irrisolto. Nel primo decennio degli anni Duemila la principale fonte di squilibrio è tornata a essere il deficit corrente americano (intorno al 6-7% del PIL). D’altra parte, il cambio gestito della moneta cinese (yuan rembimbi) impedisce una rivalutazione che sarebbe invece necessaria per moderare gli squilibri delle bilance dei pagamenti correnti.
Filosofia
Complesso organizzato di dottrine, di teorie, scientifiche o filosofiche, in coerente relazione l’una con l’altra secondo un principio unificatore.
L’idea di s. come organizzazione, come insieme di elementi interconnessi, appare già nella filosofia antica. Nella filosofia moderna la nozione è ripresa in un senso vicino a quest’ultimo da G.W. Leibniz e da C. Wolff; I. Kant qualificò ulteriormente il concetto indicando come s. «l’unità di molteplici conoscenze raccolte sotto un’unica idea». La tesi kantiana dell’unicità del principio da cui derivano tutte le conoscenze sarà privilegiata nei s. idealistici di J.G. Fichte, F.W.J. Schelling e G.W.F. Hegel, rivendicando peraltro alla filosofia come «s. unico e perfetto dello spirito umano» l’ideale di sistematicità e di scientificità. Un significato più specifico è rintracciabile nell’espressione settecentesca s. del mondo, con cui venivano indicate le teorie cosmologiche del tempo. Analogamente si indicava con il termine s. un certo insieme di tesi metafisiche o filosofiche. Gli illuministi, proprio in relazione a quest’uso, parlarono spregiativamente di esprit de système, a indicare le arbitrarie e aprioristiche costruzioni dei filosofi.
Nelle teorie delle arti, il s. delle belle arti è il tentativo di organizzare un campo unitario delle belle arti, che le distingua dalle altre attività umane in vista di una loro considerazione comune. Il primo s. delle belle arti fu proposto da C. Batteux (Les beaux-arts réduits à un même principe, 1746), secondo il quale le arti ‘maggiori’ (poesia, musica, pittura, scultura e danza) dovrebbero costituire un territorio ben delimitato, fondato sulle facoltà del genio e del gusto, e retto da una legge che dovrebbe svolgere, nella riflessione sull’arte, un ruolo simile a quello della legge di gravità nella filosofia naturale (legge che Batteux, «le Newton des beaux-arts», ritiene di trovare nel principio d’imitazione).
Fisica
S. complesso
S. composto da un numero molto grande di costituenti elementari interagenti e che quindi non può essere descritto in termini di leggi di evoluzione dei singoli costituenti, ma richiede descrizioni che fanno riferimento a valori medi o a modelli semplificati, al fine di ridurre il numero dei parametri significativi e permettere di controllarne l’evoluzione matematicamente (in particolare numericamente, mediante l’uso di calcolatori elettronici); è stato così possibile evidenziare, in taluni casi, proprietà come quella del caos deterministico (➔ caos) oppure, in altri casi, studiare i fenomeni di transizione da configurazioni ordinate a configurazioni disordinate e viceversa, come, per es., i fenomeni di autoorganizzazione e di formazione di strutture.
Scienza dei s.
Disciplina che studia con la massima generalità i s. complessi, in particolare i procedimenti matematici che li riguardano, proponendosi di elaborare modelli matematici, specialmente numerici, atti a rappresentare il comportamento di qualunque s., da quelli di interesse tecnologico a quelli di interesse biologico e anche a s. sociali, sulla base, per questi ultimi, dell’analogia funzionale tra s. sociali e s. di comunicazione, di controllo e di autoregolazione (in questo ampio significato si parla anche di teoria generale dei s.).
Per i s. disordinati ➔ disordine.
S. ottico
Definizione. Insieme di elementi rifrangenti e riflettenti (lenti, specchi ecc.), di diaframmi e di eventuali elementi accessori, coordinati a costituire uno strumento per la visione (microscopio, telescopio ecc.) o per altri scopi (proiettore, apparecchio fotografico, interferometro ecc.); si parla di s. diottrico, catottrico, catadiottrico a seconda che nella sua costituzione entrino solo elementi rifrangenti, solo elementi riflettenti oppure elementi dei due tipi.
Poiché la rifrazione e la riflessione sono fenomeni che avvengono in corrispondenza a un diottro (➔), cioè a una superficie che separi mezzi otticamente diversi, un s. ottico può essere definito anche come una successione di diottri, le cui proprietà dipendono dalla natura (rifrangente o no), dalla forma (sferica, piana ecc.), dalle dimensioni e dalla posizione reciproca dei vari diottri. Molto spesso i diottri sono piani o sferici, talora paraboloidici, raramente cilindrici; si immagina che le superfici dei diottri siano sempre regolari e lisce, almeno nei limiti delle approssimazioni dell’ottica geometrica: si assume cioè che le inevitabili irregolarità abbiano dimensioni piccole rispetto alla lunghezza d’onda media della luce (0,5 μm).
Spazio-oggetti e spazio-immagini
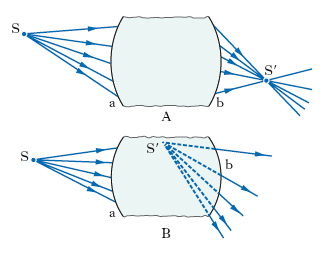
Il primo e l’ultimo diottro (a, b in fig. 1) delimitano la regione occupata dal s.; dei due semispazi al di qua del primo diottro e al di là dell’ultimo diottro, uno viene assunto come spazio-oggetti, cioè come regione in cui si propaga la luce che incide sul s., l’altro come spazio-immagini, cioè come regione in cui si propaga la luce emergente dal s. (l’arbitrarietà della scelta dell’uno o dell’altro dei due spazi come spazio-oggetti e spazio-immagini deriva dal principio dell’invertibilità del cammino dei raggi luminosi); per un s. riflettente, i due spazi ovviamente coincidono. Se il s. è stigmatico e convergente, esso trasforma un fascio omocentrico di raggi incidenti in un fascio parimenti omocentrico di raggi emergenti, di modo che tutti i raggi uscenti da un punto S dello spazio-oggetti e raccolti dal s. danno luogo (fig. 1A) a raggi che concorrono in un punto S′ dello spazio-immagini, detto immagine (reale) di S; i due punti S, S′ costituiscono una coppia di punti coniugati rispetto al sistema.
Se quest’ultimo è stigmatico e se i prolungamenti dei raggi uscenti dal s., e non i raggi stessi, convergono in un punto S′, esso prende il nome di s. divergente, in quanto (fig. 1B) S′ cade entro il s. o addirittura nello spazio-oggetti e i raggi emergenti divergono dal s.; S′, per il fatto che non cade nello spazio-immagini, cioè non è fisicamente accessibile, prende il nome di immagine virtuale.
Aberrazioni
Può accadere che un s. sia stigmatico per qualunque punto dello spazio-oggetti, e allora si dice generalmente stigmatico, oppure stigmatico soltanto per particolari punti, e si dice condizionatamente stigmatico, oppure ancora che non sia affatto stigmatico, e si dice astigmatico (da quest’ultimo termine deriva, con strano gioco di prefissi, la corrente qualifica di anastigmatico attribuita a un s. stigmatico). La mancanza di stigmatismo non è l’unica aberrazione che un s. può presentare; se infatti si considerano figure nello spazio-oggetti e corrispondenti immagini di esse date da un s., è ben raro che queste ultime siano in perfetto rapporto di similitudine con le prime: alle cause di questa mancata similitudine si dà il nome di aberrazioni (aberrazione di sfericità, distorsione ecc.: ➔ aberrazione).
Una particolare aberrazione, che, a differenza delle altre, non dipende soltanto da fattori geometrici, è il cromatismo, il quale riguarda s. in cui vi siano superfici rifrangenti che diano luogo a dispersione: un s. di tal genere è astigmatico per luci di colore diverso, nel senso che di un punto-oggetto emettente radiazioni di diversa lunghezza d’onda o diverso colore forma immagini in punti differenti e quindi di un punto emettente luce bianca forma un’immagine estesa, non puntiforme. Un s. che di per sé non presenti tale aberrazione o che sia stato corretto da essa si chiama s. acromatico. Un s. completamente esente da aberrazioni, cioè in grado di dare immagini acromatiche e simili agli oggetti, si chiama s. ortoscopico. Qualifiche particolari si hanno poi in relazione alla mancanza di una determinata aberrazione (s. acromatici, cioè, come detto, esenti da cromatismo; s. aplanatici, esenti dall’aberrazione di sfericità ecc.) o in relazione a una particolare proprietà.
S. centrati
Da quest’ultimo punto di vista notevole spicco hanno i s. centrati (o, più propriamente, s. assiali), caratterizzati dal fatto che i centri di curvatura dei diottri componenti giacciono su una medesima retta, che ha il nome di asse (ottico) del s. (per gli eventuali diottri piani il centro di curvatura è il punto all’infinito dell’asse, cioè tali diottri sono ortogonali all’asse). Lo studio dei s. centrati riesce notevolmente più semplice di quello dei s. non centrati; in particolare, tale studio può esser fatto, senza perdere di generalità, in un piano qualsiasi per l’asse ottico. Sono di seguito elencate le princiali caratteristiche, in termini di ottica geometrica, dei s. diottrici centrati, che costituiscono la categoria di gran lunga più importante dei s. ottici praticamente usati, alla quale sono riconducibili la categoria dei s. catottrici centrati e quella dei s. catadiottrici centrati.
I s. diottrici centrati sono costituiti da una successione di diottri rifrangenti con i centri di curvatura allineati su una retta, asse del sistema. Riferendoci, per semplicità, a un s. perfetto, e cioè acromatico, stigmatico, ortoscopico, esso, a prescindere dalla sua effettiva costituzione, si considera completamente determinato dal punto di vista ottico se si conoscono la giacitura dell’asse e la posizione su quest’ultimo di 4 dei 6 punti cardinali: 2 punti principali, 2 punti focali, 2 punti nodali.
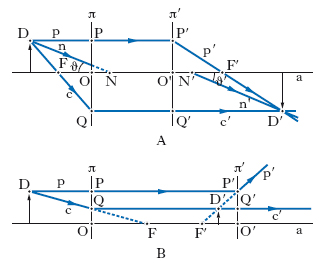
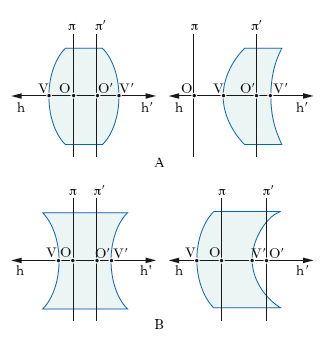
Per quanto riguarda la proprietà dei punti principali, si immagini di far passare per ciascuno di essi, O, O′ (fig. 2A) un piano ortogonale all’asse a del s.; a quest’ultimo potremo sostituire uno schema ottico equivalente in cui lo spazio-oggetti e lo spazio-immagini sono delimitati da questi due piani principali, π, π′, anziché, com’è effettivamente, dai diottri estremi del s.; in questo schema ottico, i due piani principali sono piani coniugati, un punto qualunque P di uno di essi avendo per coniugato il punto P′ in cui la parallela all’asse per P incontra l’altro piano principale; è usuale chiamare primo piano principale quello che limita lo spazio-oggetti. In conformità a quanto ora detto, se si immagina un oggetto giacente nel primo piano principale, l’immagine che di esso dà il s. giace nel secondo piano principale ed è diritta e ha la stessa grandezza dell’oggetto; i piani principali possono quindi essere definiti anche come la coppia di piani coniugati per i quali l’ingrandimento lineare trasversale (rapporto fra dimensioni corrispondenti di oggetti e immagini in piani ortogonali all’asse) vale −1 (➔ ingrandimento).
Quanto ai punti focali o fuochi, essi, a differenza dei punti principali, non sono punti fra loro coniugati, dato che sono i punti coniugati dei due punti all’infinito dell’asse: a un raggio incidente p (fig. 2A) parallelo all’asse corrisponde un raggio emergente p′ (raggio coniugato di p) che passa per il secondo fuoco, F′ (punto coniugato del punto all’infinito dell’asse nello spazio-oggetti), e, inversamente, a un raggio emergente c′ parallelo all’asse corrisponde un raggio incidente c che passa per il primo fuoco, o fuoco anteriore, F (punto coniugato del punto all’infinito dell’asse nello spazio-immagini). Come si vedrà in seguito, i fuochi cadono tutti e due o al di fuori del segmento di asse tra i punti principali oppure all’interno di tale segmento; nel primo caso si parla di fuochi reali, in quanto si tratta di punti fisicamente accessibili e per essi possono passare effettivamente raggi incidenti e raggi emergenti. Nella fig. 2A, che si riferisce appunto a fuochi reali, è indicato il procedimento per la costruzione delle immagini. Dei raggi partenti da un punto-oggetto D si considerano il raggio p parallelo all’asse, cui, come detto, corrisponde un raggio emergente p′ passante per il secondo fuoco F′, e il raggio c passante per il primo fuoco F, cui corrisponde un raggio emergente c′ parallelo all’asse (il percorso dei raggi fra punti dei piani principali, quali P, P′ e Q, Q′, è parallelo all’asse); l’immagine di D è il punto D′ in cui concorrono p′ e c′ (e ogni altro raggio coniugato di un qualunque raggio partente da D). Come la fig. 2A aiuta a comprendere, un s. con fuochi reali è convergente; sinteticamente parlando, esso dà immagini reali, capovolte, se l’oggetto giace su un piano, ortogonale all’asse, che sia distante dal primo piano principale π più della prima distanza focale, f=OF, e l’immagine si forma su un piano, ortogonale all’asse, la cui distanza dal secondo piano principale π′ è maggiore della seconda distanza focale, f′=O′F′ (l’immagine si forma all’infinito se l’oggetto è nel primo piano focale, quello ortogonale all’asse per F); dà immagini virtuali, diritte, se l’oggetto si trova tra il primo piano focale e il primo piano principale. Nell’altro caso, quello cioè in cui F e F′ cadono tra i punti principali, si parla di fuochi virtuali, in quanto per questi punti passano non raggi ma prolungamenti di raggi, come mostra la fig. 2B, che illustra il procedimento, analogo al precedente, per la costruzione geometrica delle immagini; queste ultime sono sempre virtuali, diritte, qualunque sia la posizione dell’oggetto; il s. è divergente.
Relativamente infine ai punti nodali o nodi, o centri ottici, si tratta di una coppia di punti fra loro coniugati tali che un raggio incidente n passante, effettivamente o virtualmente, per uno di essi, N (fig. 2A), dà luogo a un raggio emergente n′ passante per l’altro punto, N′, e parallelo al raggio incidente; questa proprietà vale, oltre che per i due nodi, anche per ogni coppia di punti coniugati dei due piani nodali, cioè dei due piani condotti ortogonalmente all’asse per N, N′; richiamando la nozione di ingrandimento angolare, come rapporto fra le inclinazioni sull’asse, o vergenze, ϑ, ϑ′, di raggi coniugati, i due piani nodali possono essere definiti anche come i due piani coniugati per cui l’ingrandimento angolare vale −1. Poiché bastano 4 punti cardinali per costruire le immagini date da un s., punti nodali possono sostituire a tal fine punti principali oppure punti focali.
Procedimenti di calcolo
Sono stati sviluppati potenti metodi numerici per determinare mediante calcolatori la posizione sull’asse dei punti cardinali di un s., note che siano le caratteristiche geometriche delle superfici rifrangenti o riflettenti e gli indici di rifrazione dei mezzi interessati. Come anche metodi analitici basati su ipotesi semplificatrici, le più semplici, e anche le più usate, delle quali sono quelle note come approssimazioni di Gauss, consistenti nel considerare s. di piccola apertura, cioè costituiti da diottri con dimensioni lineari piccole rispetto ai raggi di curvatura, e raggi parassiali, cioè poco inclinati sull’asse (piccole vergenze). Sotto queste approssimazioni, nel caso di s. sferici, cioè costituiti da diottri sferici o anche piani (un diottro piano può essere considerato come un diottro sferico con raggio di curvatura infinito), il procedimento di calcolo è basato sul considerare separatamente e successivamente i vari diottri: determinata l’immagine di un oggetto data dal primo diottro, come se gli altri non ci fossero, questa immagine funge da oggetto per il secondo diottro, e così via sino all’ultimo diottro. In tal modo si perviene a una relazione fra punti dello spazio-oggetti e punti dello spazio-immagini del s. espressa da una formula (formula di Huygens o di Gauss) analoga a quella del diottro semplice:
[1] formula
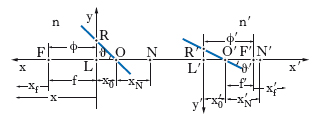
essendo x, x′ le ascisse di punti coniugati rispetto a una qualunque coppia di punti coniugati (L, L′ in fig. 3), ϕ, ϕ′ le ascisse dei fuochi. Accanto a questa, va considerata anche la relazione di invarianza
[2] formula
anch’essa analoga a quella valida per un diottro. Osserviamo che la [1] è sempre applicabile, posto che la posizione dei fuochi sia nota; tale relazione, peraltro, non è di per sé sufficiente, in quanto per la costruzione delle immagini occorre anche la determinazione dei punti principali. Associando alla [1] la [2], per le ascisse x0, x0′ di questi punti si ottiene:
[3] formula
essendo n, n′ gli indici di rifrazione dei due mezzi dalle due bande del s., y, y′ le ordinate di punti corrispondenti (R, R′ in fig. 3) di raggi coniugati passanti per i punti principali (O, O′). Una notevole semplificazione si consegue se l’origine del s. di riferimento per i punti-oggetto (x, y) e quella del s. per i punti-immagine (x′, y′) sono poste proprio nei punti principali, anziché in due generici punti coniugati; con tale scelta, dalla [3] si ha:
[4] formula
Poiché il rapporto n/n′ è senz’altro positivo, f e f′, cioè la prima e la seconda distanza focale del s., hanno lo stesso segno, e dunque, come già detto, i fuochi (F, F′) cadono tutti e due esternamente oppure internamente al segmento dell’asse compreso fra i punti principali; nel primo caso, cioè nel caso di fuochi esterni ai punti principali, le due distanze focali sono positive e il s. è convergente. Relativamente poi ai nodi, in base alle proprietà di tali punti e alle relazioni precedenti si trova per le loro ascisse rispetto ai punti principali:
[5] formula
talora, le ascisse dei punti coniugati vengono riferite ai fuochi, anziché ai punti principali (ascisse xf e xf′ in fig. 3); in luogo della [1] si ha allora la formula di Newton:
[6] formula
Il caso più frequente nella pratica è che il s. sia immerso in un mezzo omogeneo (normalmente, l’aria), di modo che gli indici di rifrazione n, n′ coincidano. In tale caso, dalle formule precedenti si ricava subito che è f=f′, xN=xN′ =0, cioè che le due distanze focali sono uguali e che i nodi cadono nei punti principali; la formula di Gauss, riferendo le ascisse ai punti principali, assume la semplice forma
[7] formula
per la costruzione delle immagini bastano i punti principali e un fuoco oppure i fuochi e un punto principale, dato che il fuoco o il punto principale mancante sono immediatamente determinabili.
Anziché prendere come punto di partenza la conoscenza dei fuochi e di due raggi coniugati qualunque per poi dedurre, secondo la [3], la posizione dei punti principali, è possibile, come detto, determinare questi ultimi direttamente dai parametri geometrici e ottici del s.; procedendo secondo tale linea è, per es., possibile studiare le lenti sferiche spesse, o non sottili, cioè s. centrati costituiti da due diottri rifrangenti sferici oppure da un diottro sferico e da uno piano. Nella fig. 4 sono schematizzati alcuni tipi di s. di tal genere e per ciascuno di essi è indicata la posizione dei piani principali π, π′; se, com’è abituale, ci si riferisce ai vertici V, V′ della lente, le ascisse dei punti principali valgono d=−rh, d′=−r′h, essendo 1/h=(n−1)+(r−r′)(n/s), con r, r′ ascisse (secondo gli assi h, h′ indicati in fig.) dei centri dei diottri, n indice di rifrazione della lente relativamente al mezzo in cui essa si trova, s distanza fra i vertici; quanto alla distanza focale si ha: f(n−1)[s(n−1)+n(r−r′)]=rr′n.
Istruzione
Il termine s. è stato a lungo riferito esclusivamente al complesso delle istituzioni scolastiche (s. scolastico) ordinate secondo i gradi e gli ordini dell’istruzione formale gestiti dallo Stato o da privati. Negli ultimi decenni del 20° sec. il ventaglio dell’offerta formativa si è notevolmente allargato, sotto la spinta crescente di una domanda di formazione in ambiti e forme diversi da quelli dell’istruzione scolastica. Anche i soggetti erogatori dei servizi sono aumentati: operano, infatti, non solo servizi gestiti direttamente dallo Stato, ma anche quelli gestiti dagli enti locali, da associazioni professionali, imprese, enti religiosi e assistenziali, fondazioni e associazioni culturali private. Per indicare l’intero ventaglio dell’offerta formativa e dei relativi servizi si è pertanto affermata l’espressione s. formativo, di cui il s. scolastico e quello della formazione professionale rappresentano i due sottosistemi più articolati. Anzi, proprio la necessità di coordinare fra loro i due principali sottosistemi ha suggerito di usare l’espressione s. formativo integrato, che sottintende la messa a punto di passaggi (passerelle) dall’uno all’altro sottosistema, nonché l’adozione della formula dei crediti formativi che rendono possibili quei passaggi.
La nozione stessa di s. si è imposta anche sotto il profilo dei modelli teorici di studio e valutazione dei complessi dispositivi coinvolti dai processi di istruzione e di formazione. Già in passato l’insegnamento scolastico è stato talvolta concepito come un insieme articolato di programmi, norme e relazioni formali all’interno di una comunità educante. Ormai, però, l’approccio sistemico non si limita a considerare la struttura dei corsi di studio, i programmi d’insegnamento, le procedure didattiche, i criteri di valutazione, lo statuto dei docenti, la conduzione degli istituti ecc.: esso deve considerare anche una serie di rapporti tra gli investimenti e la produttività dei servizi educativi, tra la competenza certificata dei docenti e i risultati scolastici degli alunni, tra le capacità di orientamento dell’azione educativa e i problemi incombenti del disagio giovanile, tra i tipi di formazione professionale e le esigenze del mondo produttivo ecc. Negli anni a cavallo fra la fine del 20° e l’inizio del 21° sec. l’esigenza di definire un quadro unitario delle opportunità formative è stata avvertita dal legislatore italiano, sebbene in modo parziale e con una terminologia non proprio definitiva. La normativa di riferimento essenziale è costituita dal d. legisl. 59/2004 riguardante la riforma della scuola dell’infanzia e del primo ciclo di istruzione e dal d. legisl. 226/2005 concernente il secondo ciclo del sistema educativo di istruzione e formazione.
Matematica
S. di equazioni
Definizione. Insieme di equazioni, in due o più incognite di qualsiasi genere (per es., numeri reali o complessi, funzioni, distribuzioni, matrici), che si pretendono simultaneamente soddisfatte. Tali equazioni possono essere ordinarie o differenziali, e si chiama soluzione un insieme di enti della stessa specie delle incognite che, posti in luogo di queste, rendono soddisfatte tutte le equazioni del s.; nel caso dei s. di equazioni differenziali, detti s. differenziali, una soluzione, che sarà un insieme di funzioni, si dice integrale del sistema. Un s. che ammette almeno una soluzione si dice compatibile o risolubile; se non ne ammette è incompatibile o impossibile (presenta cioè il caso di incompatibilità o impossibilità); un s. compatibile che ha una sola soluzione si dice determinato; se ne ha più di una si dice indeterminato. Spesso un s. di equazioni si esprime tramite una sola equazione vettoriale e le singole equazioni costituenti il sistema di partenza si dicono componenti di tale equazione. La teoria dei s. di equazioni si divide in tante teorie e tanti tipi quanti sono i tipi di equazioni (algebriche, lineari, omogenee, differenziali alle derivate ordinarie o parziali, integrali, integro-differenziali ecc.) ciascuna con i suoi sottotipi.
S. di equazioni algebriche
Insieme di equazioni algebriche, ottenute uguagliando a zero due o più polinomi in due o più indeterminate, che si chiamano incognite del s.; il prodotto dei gradi delle equazioni si dice grado del s.; l’insieme delle soluzioni, interpretato in uno spazio proiettivo come un insieme di punti, costituisce una varietà algebrica. In generale nei casi elementari la soluzione si ricerca applicando alcuni metodi di eliminazione e arrivando così a una sola equazione, detta risolvente, dalla cui risoluzione si risale alle soluzioni del s.; tra i metodi di eliminazione per risolvere tali s. i più comuni sono quelli di J. Sylvester e di L. Kronecker. Nel caso che le equazioni siano tutte lineari si ha una teoria completa per la risoluzione; per le equazioni non lineari la situazione è più complicata. Nel caso di due equazioni in due incognite numeriche, con coefficienti reali o complessi, con grado m ed n rispettivamente, le soluzioni nel campo complesso sono in numero di mn se contate con la dovuta molteplicità, e contando anche le eventuali soluzioni improprie (teorema di Bézout).
S. di equazioni differenziali
Insieme di equazioni differenziali, alle derivate ordinarie o parziali, in più funzioni incognite. Un insieme di funzioni, derivabili almeno fino all’ordine massimo che compare nel s. (detto ordine del s.), che sostituite al posto delle incognite rendono soddisfatte tutte le equazioni del s., si dice soluzione o integrale del sistema. Di solito esiste un’infinità continua di soluzioni, dipendente da un certo numero di parametri, che sono delle costanti per i s. di equazioni alle derivate ordinarie, e sono funzioni per s. di equazioni alle derivate parziali; tali costanti o funzioni possono venire determinate quando si assegnino opportunamente alcune condizioni, cioè quando si prescelgano i valori che devono assumere le incognite ed eventualmente anche alcune loro derivate in certi punti o lungo certe linee. Lo studio di una generica equazione differenziale di ordine n alle derivate ordinarie si può sempre ricondurre a quello di un particolare s. del primo ordine; il contrario non è sempre possibile; un s. di ordine k di n equazioni differenziali si può ricondurre a un s. di nk equazioni del primo ordine.
S. di equazioni lineari
S. in cui le incognite compaiono al primo grado; se le equazioni sono differenziali, compaiono al primo grado anche le derivate. La teoria per la risoluzione dei s. di equazioni lineari algebriche si basa sul teorema di Rouché-Capelli.
S. formali e assiomatici
Quando tutti gli elementi di una teoria deduttiva sono completamente simbolizzati e lo stesso calcolo logico in essa adoperato è completamente espresso, si dice che la teoria costituisce un s. formale. In un s. del genere ogni problema è formulato in termini puramente sintattici, cioè di calcolo tra i simboli senza riferimenti esterni a essi. In ultima analisi un s. formale è costituito da: a) un insieme di definizione dei segni base e delle espressioni; b) un insieme di premesse (dette assiomi o postulati); c) un insieme di regole di inferenza che consentono di trarre conclusioni dalle premesse; d) un insieme di espressioni logicamente giuste, in quanto ricavate dalle premesse mediante un numero finito di applicazioni delle regole di inferenza (teoremi o tesi). Per evitare un eccessivo appesantimento dell’apparato tecnico, la formalizzazione di una teoria non sempre è condotta fino alle estreme conseguenze; si parla perciò spesso, più in generale, di s. assiomatico. S. formali che hanno avuto una notevole importanza sono quelli di G. Frege, di B. Russell e A.N. Whitehead, di J. Łukasiewicz, di D. Hilbert e W. Ackermann, di D. Hilbert e P. Bernays.
S. ipotetico-deduttivo
Teoria matematica che si costruisce astrattamente fissando alcuni concetti primitivi, e alcune proposizioni a essi inerenti (s. di assiomi o di postulati). I concetti primitivi, che in generale rispecchiano concetti intuitivi, spesso derivanti dall’esperienza elementare, non vengono definiti, bensì vengono associati a un insieme i cui elementi sono, tutti e soli, quelli che soddisfano il s. di assiomi (definizione implicita): tale s. di assiomi è pertanto costituito dalle proprietà caratteristiche degli elementi di quell’insieme. Ovviamente il s. di assiomi deve essere coerente (o compatibile), cioè tale che due qualsiasi asserzioni logicamente dedotte da essi non siano contraddittorie. L’insieme di queste asserzioni dedotte costituisce il s. ipotetico-deduttivo. Non è necessario che questi postulati enuncino proprietà intuitive o evidenti; anzi può succedere che qualche postulato o qualche proposizione dedotta sia in contrasto con certe verifiche sperimentali della fisica; ciò significa semplicemente che quel s. ipotetico-deduttivo, pur essendo logicamente coerente, non è un modello matematico astratto dello spazio fisico. Normalmente si richiede che i postulati siano indipendenti, cioè che nessuno di essi sia conseguenza degli altri; talvolta invece, per poter semplificare certe dimostrazioni, si parte da un s. di assiomi sovrabbondante.
Nei s. ipotetico-deduttivi usati nella pratica, i postulati e i concetti primitivi sono suggeriti dall’intuizione, e si riferiscono agli aspetti fondamentali della teoria; inoltre la deduzione non è puramente meccanica, bensì è indirizzata verso i fini che la teoria si propone, implicitamente presenti già nel s. di assiomi. Nel s. ipotetico-deduttivo spesso è utile introdurre altri concetti sussidiari tramite loro proprietà o loro relazioni con i concetti primitivi, e la frase che precisa tale nuovo termine è una definizione. Un tipico esempio di s. ipotetico-deduttivo è l’aritmetica basata sui postulati di Peano: i numeri naturali (cioè interi positivi) soddisfano evidentemente tali postulati e qualsiasi proposizione da essi dedotta; viceversa qualsiasi teorema dell’aritmetica è deducibile da tali postulati; pertanto i numeri naturali costituiscono un modello del concetto astratto di ‘numero’. Tuttavia anche altre classi di enti, come le traslazioni su una retta aventi verso concorde e ampiezze multiple di una data, soddisfano i postulati, e costituiscono perciò un altro modello del concetto di ‘numero’. L’aritmetica coglie pertanto le proprietà comuni di tutti questi modelli. Altro esempio di s. ipotetico-deduttivo è la teoria assiomatica degli insiemi, la quale in alcune esposizioni ha come unico concetto primitivo il significato della frase ‘è elemento di’. Altro esempio è la geometria secondo Hilbert.
S. dinamici
S. lineari e non lineari
Un s. dinamico è governato da una legge di evoluzione deterministica che specifica il suo stato al tempo t, rappresentato matematicamente da un vettore x(t), a partire dal suo stato, x(0), all’istante iniziale: x(0)→x(t). Le più comuni leggi di evoluzione deterministiche sono le equazioni differenziali: dx/dt=f(x), e le mappe (o applicazioni), nelle quali il tempo assume valori discreti: x(t+1)=g(x(t)). I s. dinamici si dividono in due grandi classi: s. lineari, in cui le gi e le fi sono funzioni lineari delle xj; s. non lineari. Nel primo caso è sempre possibile risolvere le equazioni in modo esplicito con i metodi dell’algebra lineare. Per un s. non lineare, a parte il caso eccezionale dei s. integrabili, non è possibile trovare le soluzioni e inoltre si possono avere comportamenti non banali, come moti aperiodici e caos deterministico. Indipendentemente dalla difficoltà di trovare la soluzione esplicita è possibile classificare, almeno qualitativamente, il comportamento di un s. dinamico in base alla natura del suo attrattore e al valore degli esponenti di Ljapunov.
Attrattore
L’attrattore è il luogo dei punti percorsi dalla traiettoria, dopo un transiente sufficientemente lungo, che gode della seguente importante proprietà: se il punto x(0) appartiene all’attrattore allora vi appartiene anche x(t); in termini matematici si dice che l’attrattore è invariante per evoluzione temporale. Nei s. dinamici che hanno un attrattore, detti dissipativi, il volume nello spazio delle fasi si contrae nel corso dell’evoluzione; matematicamente questa proprietà è verificata se Σi∂fi/∂xi<0, nel caso di equazioni differenziali. Analogamente, una mappa è detta dissipativa se |detA|<1, dove gli elementi della matrice A sono Aij=∂gi/∂xj. La proprietà di contrarsi del volume nello spazio delle fasi è abbastanza comune, anche se esiste una notevole eccezione costituita dai s. meccanici senza attrito (s. hamiltoniani). L’esempio più semplice di attrattore si ha in s. con un punto fisso stabile. Un punto fisso, x~, è determinato dall’equazione: x~=g(x~) per le mappe, e f(x~)=0 per le equazioni differenziali. Il termine punto fisso deriva dal fatto che se all’istante iniziale x(0)=x~ allora si avrà x(t)= x~ per ogni tempo t>0. Se un punto fisso è stabile, x(t) si avvicina molto rapidamente a x~, se x(0) non è lontano da x~. La stabilità di un punto fisso può essere determinata studiando gli autovalori della matrice Aij, nel caso delle mappe, o Bij=∂fi/∂xj, nel caso delle equazioni differenziali, con le derivate che definiscono le matrici calcolate nel punto fisso x~. Un caso familiare di punto fisso stabile si ha per il pendolo con attrito in cui l’attrattore è un solo punto, il punto fisso stesso. L’attrattore più semplice dopo il punto fisso è il ciclo limite: in questo caso la traiettoria si avvicina velocemente a una curva chiusa (ciclo) e quindi, dopo un transiente, si ha un moto praticamente periodico. Oscillazioni periodiche (o quasiperiodiche) con N frequenze corrispondono al moto su un toro N-dimensionale. Nei casi considerati il moto è regolare e i corrispondenti attrattori sono oggetti regolari: un punto, una curva chiusa, una superficie o ipersuperficie.
Un s. caotico, nel quale si ha una forte dipendenza dalle condizioni iniziali, ha un attrattore che non è un oggetto regolare, ma ha una struttura generalmente molto complicata. In questo caso si parla di attrattore caotico o, usando la terminologia introdotta da D. Ruelle, attrattore strano (➔ anche complessità). Se un s. è dissipativo il suo attrattore non può occupare una regione con volume finito, infatti se così fosse l’attrattore non sarebbe invariante sotto l’evoluzione temporale. Sfruttando il teorema di esistenza e unicità della soluzione delle equazioni differenziali è possibile mostrare che l’attrattore di un s. caotico a tre dimensioni, la cui evoluzione è data da un’equazione differenziale, non può essere contenuto su una superficie regolare esprimibile nella forma F(x,y,z)=0. Si ha quindi che l’attrattore deve avere un volume nullo in R3 e tuttavia non può essere una superficie liscia; l’unica possibilità è qualcosa di intermedio: una superficie ‘molto rugosa’. Questa proprietà è generale: un attrattore strano è in genere un oggetto non regolare con dimensione frattale non intera.
Gli esponenti caratteristici di Ljapunov (o, semplicemente, esponenti di Ljapunov) λi forniscono utili informazioni sulla natura di un attrattore. In un s. dissipativo d-dimensionale, una sfera d-dimensionale con centro x(0), appartenente all’attrattore e di raggio molto piccolo ∊, sotto l’evoluzione temporale indotta dalle equazioni del moto si deforma in un’ellisse il cui volume diminuisce nel tempo. Se al tempo t l’ellisse ha semiassi li(t), gli esponenti caratteristici di Ljapunov λ1, λ2, λ3,...,λd (numerati in modo progressivo decrescente λ1≥λ2≥λ3...) sono definiti nel seguente modo: λi=(1/t)ln[li(t)/∊], dove t deve essere preso molto grande. Per poter parlare di ellisse, nella precedente equazione si deve considerare prima il limite di piccoli valori di ∊ e poi di grandi valori di t, in modo che li(t) non sia mai troppo grande. Valgono le seguenti proprietà: a) nei s. dissipativi si ha Σiλi<0; b) nei s. la cui evoluzione è data da un’equazione differenziale, almeno un λi è nullo se non ci sono punti fissi stabili. Per mezzo degli esponenti di Ljapunov è possibile caratterizzare un attrattore: a) per un punto fisso stabile tutti i λi sono negativi; b) in un ciclo limite λ1=0 e λi<0 per i>1; c) nel moto su un toro N-dimensionale λ1=λ2 = ... = λN=0 e λi<0 per i>N; d) in un s. caotico almeno un esponente caratteristico di Ljapunov è positivo. Gli esponenti di Ljapunov non solo caratterizzano un s. dinamico dal punto di vista qualitativo, bensì danno importanti informazioni su proprietà quantitative della dinamica caotica. Per es., la somma degli esponenti di Ljapunov positivi K=∑i:λ.>0λi è chiamata entropia di Kolmogorov-Sinai, o entropia metrica, ed è una misura del grado di caoticità del sistema (➔ entropia). 4.4 Complessità algoritmica. È possibile evidenziare la stretta analogia tra s. con caos deterministico e s. in cui è presente una componente casuale esterna mediante il concetto di complessità algoritmica, introdotto da A. Kolmogorov e G.J. Chaitin e definito nel seguito. Data una successione di N numeri x1, x2, x3, ..., xN (per semplicità si suppone che ogni xk possa assumere solo i valori 0 e 1), si considera il più corto programma per calcolatore, cioè quello con meno istruzioni, tra tutti quelli che generano questa successione; indicando con K(N) il numero di queste istruzioni, si definisce complessità algoritmica, C, della successione la quantità: C=limN→∞K(N)/N. Se esiste una regola semplice, esprimibile con poche istruzioni, la complessità è nulla, nel caso non esista alcuna regola diversa dall’elencazione esplicita della sequenza si ha la complessità massima Cmax; valori di C intermedi tra 0 e Cmax corrispondono a situazioni con regole non evidenti. Questa definizione di complessità è naturale in problemi connessi alla trasmissione di messaggi. È concettualmente importante mostrare che una successione può essere complessa anche se generata da un s. dinamico deterministico. Per es., nel s. dinamico retto dall’equazione: y(t+1)=2y(t) [mod 1] si può definire la successione x1, x2, x3, ..., xN prendendo xt=0 se y(t)<1/2 e xt=1 se y(t)≥1/2. La successione così costruita non è altro che un modo diverso di scrivere y(0): infatti ogni numero y(0) contenuto nell’intervallo [0,1] può essere espresso nella forma y(0)=a1/2+a2/4+... +an/2n+..., dove ogni an vale 0 oppure 1; xn risulta essere l’n-ma cifra binaria di y(0) e la complessità della successione data è quindi strettamente legata a quella di y(0). Potrebbe sembrare che la complessità algoritmica della successione generata nel modo appena esposto sia nulla, in quanto ottenuta da una regola esprimibile con un programma contenente poche istruzioni. Ciò non è vero perché il programma deve specificare anche y(0), quindi per ottenere una successione di lunghezza N si devono specificare N cifre binarie di y(0). Si ha allora che da una generica condizione iniziale y(0) si genera una successione che non è distinguibile da una successione ottenuta lanciando ripetutamente una moneta: la complessità algoritmica risulta essere la massima possibile. Questo esempio mostra come un comportamento complesso non debba considerarsi necessariamente associato al caso ma anche al caos deterministico e quindi il margine tra regole probabilistiche e deterministiche non è netto. In generale la complessità C di una successione, cioè il numero medio di bit per unità di lunghezza, necessari per trasmettere (con una data precisione) la successione, è strettamente collegata alle proprietà del s. dinamico da cui è generata attraverso la relazione: C=K/ln2, dove K è l’entropia di Kolmogorov-Sinai.
Teoria dei sistemi
La teoria dei s. (detta anche scienza dei s.) studia il comportamento di insieme di elementi interconnessi (funzionali o concreti), detti entità; ogni entità è caratterizzata da: a) grandezze (dette anche variabili) di ingresso provenienti da altre entità del s. o dall’esterno; b) grandezze di stato che descrivono la situazione in cui si trova l’entità; c) grandezze di uscita, il cui valore dipende da ingressi e stato, indirizzate verso altre entità del s. o verso l’esterno. Le grandezze di ingresso provenienti dall’esterno sono dette anche esogene, quelle interne al sistema endogene. Le grandezze esogene possono essere di vario tipo: grandezze controllate da una o più entità decisionali esterne che cercano di influenzare l’evoluzione del s. (grandezze di controllo); uscite di altri s. che evolvono indipendentemente o la cui evoluzione è legata a quella del s. in esame, disturbi dovuti generalmente a effetti combinati di entità esterne non facilmente caratterizzabili in termini di sistema. Le grandezze di ingresso provenienti dall’esterno sono dette ingressi del s., quelle di uscita dirette verso l’esterno sono dette uscite del sistema. La suddivisione delle grandezze che interagiscono con l’esterno in ingressi e uscite corrisponde generalmente a relazioni causa-effetto e viene detta orientamento del sistema. Gli elementi che formano il s. possono corrispondere a funzioni svolte (operazioni di trasformazione di materiali e/o informazioni) e/o a componenti fisici.
I s. vengono detti aperti se vi sono interazioni con l’esterno (attraverso ingressi e uscite), si dicono chiusi se la loro evoluzione non dipende da grandezze esterne (ovvero non vi sono ingressi, possono invece esservi uscite in quanto alcune grandezze possono essere misurate e tale misura essere portata all’esterno). Se le uscite di alcune entità del s. vengono misurate da un sottosistema di misura e, dopo opportune elaborazioni e trasformazioni, vengono utilizzate come ingressi in modo da formare cicli (il caso più semplice è quando una uscita di una entità viene riportata in ingresso della stessa entità), si dice che vi è una retroazione (feedback); l’evoluzione temporale di un s. con controreazione è un problema largamente studiato nella tecnica, in particolare nell’analisi della stabilità.
In un s. l’evoluzione dello stato delle varie entità dipende dallo stato iniziale e dagli ingressi del s., quella delle uscite del s. dallo stato e dagli ingressi. Se le funzioni che legano lo stato a un certo istante a stato iniziale e ingressi, e le uscite a ingressi e stato, sono lineari, il s. è detto lineare, in caso contrario è detto non lineare; se le funzioni sono lineari rispetto allo stato e lineari rispetto all’ingresso ma non lineari rispetto a entrambi (ovvero se compaiono dei prodotti fra variabili di stato e di ingresso), il s. è detto bilineare; se il tempo è discretizzato e le grandezze in esame sono considerate solo in particolari istanti o intervalli temporali (sia per l’introduzione di una approssimazione, sia perché ciò corrisponde alla situazione reale), il s. è detto a tempo discreto; se anche i valori che possono assumere le grandezze del s. sono discretizzati o appartenenti a un insieme finito, il s. è detto discreto; se alcune grandezze del s. sono variabili aleatorie, il s. è detto stocastico; se le funzioni che legano ingressi, stato e uscite sono equazioni differenziali alle derivate parziali, il s. è detto a parametri distribuiti; se la struttura delle funzioni che legano ingressi, stato e uscite può essere modificata (o comunque varia nel tempo), il s. è detto a struttura variabile (ed è generalmente non lineare).
La scienza dei s. offre una metodologia generale per la rappresentazione e l’analisi di situazioni in diversi ambiti applicativi, e per lo studio di possibili modalità di intervento per ottenere comportamenti desiderati del s., anche se le difficoltà di analisi ed elaborazione diventano spesso troppo elevate per utilizzazioni pratiche. Applicazioni significative sono state sviluppate in quasi tutti i settori della tecnica.
Metrologia
S. di unità di misura
Insieme delle unità di misura delle grandezze assunte come fondamentali e di quelle derivate. Nell’ambito della meccanica un s. di unità si dice assoluto oppure pratico (o tecnico) a seconda che siano assunte, come grandezze fondamentali, lunghezza, tempo e massa oppure lunghezza, tempo e forza. Sono s. assoluti il s. CGS (cm, g, s) e il s. MKS (m, kg, s). Da quest’ultimo, con l’aggiunta dell’ampere, deriva il s. MKSA dell’elettromagnetismo, e, con l’ulteriore aggiunta del kelvin, della mole e della candela, il S. Internazionale (SI), universale e definitivo per tutti gli usi scientifici e tecnici (➔ unità).
S. metrico decimale
S. di unità di misura che prende a base delle unità di lunghezza il metro, di area il metro quadrato, di volume il metro cubo; i multipli e i sottomultipli delle dette unità fondamentali si ottengono da esse per moltiplicazione o divisione per potenze di 10.
Politologia e scienze sociali
Modo in cui è organizzato un settore della vita di una collettività, di una nazione, o anche una sua istituzione, una sua struttura.
S. elettorale e s. partitico
Il s. elettorale e il s. partitico costituiscono due parti rilevanti, fra loro strettamente interrelate, rispetto al s. politico complessivo nel quale sono inserite e del quale contribuiscono a definire la forma del regime nonché il funzionamento degli strumenti di rappresentanza e decisione politica. In particolare, si intende per s. partitico l’insieme delle strutture di partito e delle loro interazioni reciproche in vista della conquista e dell’esercizio del potere politico; mentre il s. elettorale è a sua volta l’insieme delle procedure e dei meccanismi di rappresentanza politica, attraverso i quali si provvede a regolare in senso democratico la competizione fra partiti.
Per quanto riguarda la genesi storica dei s. di partito, occorre considerare, da una parte, il processo di strutturazione dei partiti nella società, per cui si realizza un notevole rafforzamento dell’organizzazione dei partiti e del loro radicamento sociale, in conseguenza dell’allargamento del suffragio e della formazione del partito di massa; dall’altra, il processo di specializzazione e di autonomia funzionale del s. partitico rispetto al s. politico. Laddove, al contrario, permangono rapporti di intercompenetrazione e sovrapposizione fra Stato e partiti – come nei casi dei s. a partito unico, ma anche nelle esperienze di degenerazione partitocratica delle democrazie competitive – alla lunga il s. dei partiti tenderà a controllare e assorbire ogni processo di sviluppo politico. Le prospettive di analisi comparata dei s. di partito si articolano su 2 piani: quello della tipologia dei s. partitici a seconda delle coalizioni di governo e delle maggioranze parlamentari che esso è in grado di esprimere (e quindi, indirettamente, del grado di stabilità o governabilità che favorisce); e quello dei condizionamenti che le procedure elettorali possono esercitare sulla configurazione del s. partitico. Sotto il primo profilo si possono distinguere nei s. politici occidentali alcune situazioni generali. Accanto alle modalità di alternanza al potere fra 2 partiti o 2 coalizioni di partiti (com’è nel caso paradigmatico del bipartitismo inglese e nella Francia della V Repubblica), vi sono casi di semi-turn-over, cioè di ricambio parziale, nei quali il cambiamento della coalizione di governo è determinato dagli spostamenti ‘a pendolo’ di uno o più partiti dall’uno all’altro schieramento, oppure di ricambio periferico con alcuni partiti sempre al governo e altri in relativa, parziale rotazione (l’esempio emblematico è quello dei governi italiani nel secondo dopoguerra), o ancora casi di grande coalizione (verificatisi, in particolare, in Austria, Germania e Italia) o infine casi di predominanza, dati da situazioni in cui l’opposizione è tanto frantumata da non potersi costituire come alternativa di governo e, per contro, le coalizioni al potere danno spesso vita a governi di minoranza. Sotto l’altro profilo, delle connessioni fra s. elettorale e s. dei partiti, l’opera pionieristica è senz’altro quella di M. Duverger (Les partis politiques, 1951), il quale collegò i sistemi maggioritari al bipartitismo e i sistemi proporzionali, insieme al doppio turno, al multipartitismo. Ma le tesi di Duverger hanno subito tali e tante confutazioni empiriche da indurre a capovolgere il senso delle relazioni fra s. elettorale e s. partitico, attribuendo piuttosto a quest’ultimo il ruolo di variabile indipendente. Ciò non significa tuttavia che le modificazioni del s. elettorale siano del tutto ininfluenti (a determinate condizioni) sul s. partitico e più in generale sul s. politico. Più specificamente questi effetti possono essere valutati con riferimento a 3 aspetti: il grado di manipolazione delle scelte elettorali (quanto e come gli elettori sono indotti a votare in un certo modo), il grado di dis;rappresentatività (in termini di sovra- o sottorappresentanza dei partiti), e il formato del s. partitico (numero dei partiti).
A loro volta, i s. elettorali vanno considerati nell’insieme dei loro elementi costitutivi, che sono: i modi di strutturazione della scelta elettorale attraverso il tipo di scheda (per es., voto di lista o voto individuale); l’ampiezza delle circoscrizioni o collegi (il numero dei seggi da assegnare per ciascuno di essi, da cui la differenza di base fra collegi uninominali e collegi plurinominali); la formula di conversione dei voti in seggi. Così considerati, i s. elettorali possono disporsi schematicamente lungo un asse ideale i cui estremi sono rappresentati, per un verso, dai s. forti (quelli che realizzano il massimo potenziale manipolativo, disrappresentativo e riduttivo sul s. dei partiti) e per l’altro dai s. deboli, nei quali questo potenziale è ridotto ai livelli minimi. Sul lato dei s. forti si collocano gli ordinamenti elettorali di tipo maggioritario, che tendono a massimizzare lo scarto fra voti e seggi. Solitamente basati su collegi uninominali, i s. maggioritari si distinguono nelle formule del plurality (maggioranza relativa), del majority (maggioranza assoluta) e del doppio turno, che tuttavia è spesso il risultato della combinazione di più formule in 2 successive tornate elettorali con una soglia di esclusione (o clausola di sbarramento) fra il primo e il secondo turno che provvede a ridurre drasticamente la competizione di liste e candidati in diversi modi: per es., attraverso un quorum di ammissione, o attraverso il vero e proprio ballottaggio che promuove solo i primi 2 candidati più votati (come avviene in Italia, dal 1993, per l’elezione dei sindaci nelle città più grandi). Sul lato opposto dei s. deboli si colloca la svariata gamma degli ordinamenti di tipo proporzionale, che tendono a ripartire i seggi fra i diversi contendenti in modo che rispecchino il più fedelmente possibile la distribuzione delle rispettive quote elettorali. La formula che adotta il criterio più puro di proporzionalità è quella detta del ‘quoziente naturale’ nell’ambito di un collegio unico nazionale (come, per es., nei Paesi Bassi, e in Israele fino al 1992). Fra questi estremi oscilla una grande varietà di s. misti, che contengono elementi correttivi in senso maggioritario o proporzionale: in particolare s. prevalentemente maggioritari, temperati da misure di garanzia per le minoranze e s. prevalentemente proporzionali che prevedono meccanismi di rafforzamento delle maggioranze (come, per la verità, fanno in diversa misura tutti i metodi di ripartizione dei seggi adottati dalle formule proporzionali, e come più esplicitamente si ottiene attraverso un qualche premio di maggioranza). Circa l’efficacia operativa del s. elettorale in ordine alla manipolazione delle scelte di voto e alla disrappresentatività, vale una regola molto semplice: le formule maggioritarie tendono, per definizione, a esercitare una pressione manipolativa e disrappresentativa, mentre quelle proporzionali tendono al contrario a non forzare la competizione elettorale e tanto più vi riescono quanto più ampi sono i collegi circoscrizionali nei quali operano.
Con riferimento invece all’attitudine riduttiva sul numero dei partiti, bisogna distinguere se le influenze del s. elettorale si producono su s. partitici forti o deboli, vale a dire su s. già strutturati e consolidati storicamente, ovvero su s. ancora in fase di formazione oppure ormai in crisi di decomposizione. Si può schematicamente ricavarne che, in presenza di s. partitici forti, un s. elettorale di tipo maggioritario può esercitare effetti riduttivi sul numero dei partiti a livello delle singole circoscrizioni, ma sul piano nazionale la sua efficacia si limita soltanto a congelare la situazione esistente (nel senso che se già esiste un s. bipartitico, questo verrà preservato); mentre un s. elettorale di tipo proporzionale ha esclusivamente un potere riproduttivo, quasi fotografico, sul s. partitico nel cui ambito è applicato (quindi non crea frammentazione, semmai, semplicemente, non l’ostacola). Al contrario, in presenza di s. partitici deboli, possono ben poco sia le formule maggioritarie sia e ancora di più quelle proporzionali. Per concludere, l’impatto degli strumenti elettorali sul s. partitico, seppure possa risultare di qualche efficacia operativa in talune circostanze e a determinate condizioni, è comunque condizionato da tutta una serie di fattori e di variabili storiche, culturali e istituzionali da cui dipende, in effetti, il successo di ogni strategia di mera ingegneria e alchimia politica.
S. politico
Insieme delle interrelazioni fra unità politicamente significative (individui, gruppi, strutture) e fra processi attraverso i quali si producono decisioni che riguardano una determinata collettività. Nella sua accezione più estesa, il concetto di s. politico è venuto a sovrapporsi alla nozione di Stato, propria della tradizione giuspubblicistica e filosofica e ritenuta inadeguata a descrivere e spiegare la molteplicità delle dimensioni e dei fenomeni che caratterizzano la politica nel mondo contemporaneo. Il s. politico funziona sostanzialmente come un meccanismo complesso che risponde alle sfide del proprio ambiente (sociale, economico, internazionale), vi si adatta attraverso equilibri omeostatici e cerca di modificarlo attraverso ‘allocazioni autoritative di valori’, cioè decisioni vincolanti per l’intera collettività, che distribuiscono risorse simboliche e materiali con una buona probabilità che queste vengano accettate e attuate dai membri della comunità politica. I processi attraverso i quali si realizza questa attività consistono nell’immissione di domande e sostegno (input), nella loro conversione in decisioni (output), nella valutazione di queste attuazioni (outcome) e negli effetti di retroazione che esercitano sulle nuove domande e sulle immissioni di sostegno (feedback). Ogni s. comunica dunque con l’ambiente cui è esposto e da cui riceve stimoli, mantenendo propri confini che delimitano la sfera politica dalle altre sfere della vita sociale: e la misura di questi confini segna il grado di rilevanza e di penetrazione del s. politico nella società, nel mercato o nell’arena internazionale (per es., in regimi a tutti gli effetti ‘interventisti’, i confini del s. politico saranno massimamente dilatati; viceversa, in regimi di tipo liberista gli stessi confini tenderanno a restringersi nella configurazione di uno ‘Stato minimo’). Infine, ogni s. politico comprende al suo interno più sottosistemi (per es., partitico, parlamentare, giudiziario ecc.) che interagiscono fra loro e con il s. politico cui appartengono, assumendone le stesse modalità di funzionamento, ma non anche la stessa cogenza e lo stesso ambito di efficacia per quanto riguarda gli output decisionali, di fatto destinati ai propri membri e non a tutti i membri della comunità politica.
I s. politici hanno un proprio ciclo di sviluppo durante il quale si consolidano, si modificano – fino ad assumere nuove configurazioni morfogenetiche (come avviene, per es., in seguito a processi anche radicali di cambiamento) – o possono estinguersi per effetto, per es., di rivolgimenti rivoluzionari. In conclusione, la prospettiva sistemica ha fornito contributi teorici importanti alla scienza politica, soprattutto per quanto riguarda l’analisi comparata orientata empiricamente, anche se presenta rischi di degenerazione in senso olistico quando se ne perda di vista la valenza essenzialmente euristica per assumere il s. politico non come modello ma, impropriamente, come realtà a sé stante.
S. sociale
Nella tradizione analitica delle scienze sociali, l’organizzazione complessiva dei rapporti e delle istituzioni collettive e le interazioni che in questa si stabiliscono secondo la logica compositiva che lega le parti al tutto. Nell’analisi sistemica della società si distingue un modello di riferimento di tipo analogico da uno di tipo logico e formale. Il s. analogico consiste nel rappresentare una realtà complessa attraverso il confronto con una realtà più semplice, descritte entrambe in termini di s., che si presume possa avere alcune proprietà simili a quelle che sono state scelte come oggetto di studio. In questo senso, l’idea di società elaborata dalla ‘protosociologia’ (da autori come A. Comte, H. Spencer, É. Durkheim) è spesso basata sul ricorso alla metafora dell’organismo vivente o alla similitudine con i s. meccanici (la piramide, la scala, la bilancia, l’orologio). A differenza di quello analogico, il s. formale è una costruzione logica e simbolica di una situazione reale, elaborata mentalmente, che non ricorre al paragone con realtà di altra natura né presume di valere essa stessa come realtà distinta. La ricostruzione teoricamente più sofisticata in questo senso si deve a T. Parsons e alla scuola struttural-funzionalista americana degli anni 1950, secondo cui il punto di partenza di ogni analisi della società è dato dallo studio dell’azione sociale, considerata appunto come s. nel contesto delle interdipendenze che la legano ad altri s. sottordinati attraverso un ordine di controllo cibernetico che procede, in linea ascendente, per contenuto di informazione e, in linea discendente, per contenuto di energia. L’analisi sistemica della società costituisce, in questa chiave, un modello di astrazione logica che serve a organizzare il dato empirico in proposizioni generali, che abbiano a loro volta la proprietà di essere connesse secondo relazioni di interdipendenza funzionale.
S. internazionale
Il complesso delle relazioni tra gli attori internazionali. In passato, vari s. internazionali si sono sviluppati, indipendentemente l’uno dall’altro, in regioni diverse del pianeta; oggi, per l’elevato grado di interdipendenza derivante da trasporti e comunicazioni di massa, il s. internazionale è globale. Fra gli attori, si distinguono in primo luogo gli Stati, che hanno un ruolo predominante in quanto detentori dei maggiori attributi della sovranità, quali, per es., il controllo del territorio e l’uso legittimo della forza; in secondo luogo, le organizzazioni internazionali, sia universali (per es. l’ONU), sia regionali (per es. l’OCSE). Il periodo post-bellico ha visto anche la nascita di svariate organizzazioni di carattere politico-militare, imperniate sulla rivalità tra USA e URSS. Tra quelle guidate dai primi, si ricordano la NATO (in Europa occidentale), ancora in vigore, la CENTO (in Asia sud-occidentale) e la SEATO (in Asia sud-orientale), oggi dissolte. L’URSS aveva risposto al riarmo della Repubblica Federale di Germania e alla sua integrazione nella NATO creando il Patto di Varsavia nell’Europa centro-orientale, poi sciolto a seguito dei mutamenti politici intervenuti dopo il 1989. Tra le organizzazioni internazionali si annoverano anche associazioni settoriali tra Stati che condividono particolari interessi economici o di mercato: per es., l’Organizzazione dei paesi produttori di petrolio (OPEC). Vi è poi l’emergere di comunità sovranazionali, come l’Unione Europea, alle quali gli Stati membri hanno devoluto alcuni attributi della propria sovranità. Infine, possono considerarsi alla stregua di soggetti del s. internazionale anche alcune grandi società multinazionali.
Un s. internazionale è definito soprattutto dal grado della sua ‘polarizzazione’: unipolare, bipolare o multipolare. Si ha un s. unipolare quando un solo attore (in passato una potenza imperialistica, oggi una superpotenza o un’alleanza globale) ha la capacità di influire sullo sviluppo del sistema. Si ha un s. bipolare quando due attori prevalenti sulle altre unità del s., e i loro eventuali alleati, bilanciano reciprocamente le proprie risorse di potere, mantenendo comunque una situazione di egemonia all’interno delle rispettive sfere di influenza. Il s. bipolare ha prevalso, anche se sotto forme sempre meno totalizzanti, dalla fine della Seconda guerra mondiale al 1989, anno che ha visto la disgregazione della sfera di influenza sovietica. In un s. multipolare le maggiori potenze manovrano per aumentare la propria influenza a discapito di quella delle altre, alternando forme di collaborazione e di competizione. Quando prevale la collaborazione, si parla di ‘concerto delle potenze’, come nel periodo immediatamente successivo al Congresso di Vienna del 1815. Quando prevale la competizione, si parla di ‘equilibrio di potere’, come dalla seconda metà del 19° sec. fino alla Seconda guerra mondiale.
Tecnica
S. articolato
Nella meccanica, genericamente, insieme di corpi rigidi vincolati tra loro mediante cerniere sferiche o cilindriche destinato a particolari impieghi tecnici. I corpi rigidi costituenti il s. sono generalmente sbarre, rettilinee o curvilinee. Gli impieghi più frequenti di tali s. si hanno nella cinematica applicata, nella realizzazione di molti meccanismi, e nelle costruzioni, dove i s. articolati (detti anche reticolari) vengono usati per coperture (a capriata, a volta, a cupola), per mensole, pensiline, piloni, travature varie, dette in tal caso travature reticolari. Ove concorrano particolari condizioni di vincolo (cerniere cilindriche ad assi normali a un medesimo piano) e particolari condizioni di simmetria (geometrica, materiale e relativa alla sollecitazione) un s. articolato può essere schematizzato come un s. piano; in tal caso un’asta viene assimilata a un segmento e una cerniera a un punto materiale detto nodo. Un s. articolato è di solito vincolato ad altri corpi, generalmente fissi, mediante cerniere, appoggi ecc., ed è pertanto sottoposto a un insieme di vincoli interni ed esterni. Se i vincoli interni sono tali da non consentire al s., quando esso sia liberato dai vincoli esterni, che una ben determinata configurazione, il s. si suole dire indeformabile; si dice invece deformabile nel caso opposto.