spinta

Fisica

Forza che si esercita sulla superficie esterna di un corpo, con direzione normale o no alla superficie medesima, tale che il corpo risulti in qualche modo sollecitato a spostarsi; la s. idrostatica (o s. di Archimede) è quella esercitata da un fluido su un corpo in esso immerso (➔ Archimede).

Con diverso, specifico significato, la s. è anche la forza esercitata dal propulsore di un qualsiasi veicolo che si muova in un fluido (nave, sommergibile, aereo, missile ecc.) o nello spazio interplanetario (missili, veicoli spaziali). La s. serve sia a vincere la resistenza al moto del veicolo, sia a imprimergli un’accelerazione.

Psicologia

In psicopatologia, analogamente al tedesco Schub e al francese poussée, accensione acuta di un processo psicotico, specie schizofrenico, in contrasto con un suo decorso cronico, uniforme, con modeste oscillazioni della sintomatologia; in psicanalisi, lo stesso che pulsione (s. alla fuga, al vagabondaggio; le s. compulsive degli ossessivi; le s. suicidarie).

Tecnica

Nella scienza delle costruzioni il termine s. è usato con particolare riferimento a due casi di preminente interesse nella statica: la s. delle terre e la s. delle strutture ad arco, a volta, a telaio ecc., cioè l’azione che queste strutture (dette per questo anche strutture spingenti) esercitano sulle strutture su cui sono impostate.

S. delle terre

fig.

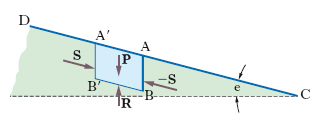
La s. delle terre è l’azione di un terrapieno sulle strutture che lo sostengono. La valutazione preventiva della s. è perciò importante soprattutto nella progettazione dei muri di sostegno (➔ muro); a tale valutazione, sempre piuttosto complessa, si può pervenire dopo prelevamento di campioni per la determinazione del peso per unità di volume della terra, dell’angolo di attrito e dell’eventuale coesione. La teoria del masso illimitato propone la determinazione del valore della s. S risultante delle azioni che si trasmettono, entro un ammasso illimitato di terra attraverso una parete verticale (come la parete di traccia AB in fig.). La terra è supposta perfettamente omogenea e totalmente esente da coesione (condizione questa che si verifica, per es., per le sabbie asciutte e non troppo costipate). Il masso è superiormente limitato da un piano CD (piano di campagna), inclinato sull’orizzontale di un angolo ε. Per ragioni di simmetria, pensando isolato nel masso un prisma di terra come quello di traccia ABB′A′ in fig. (e lunghezza unitaria), si stabilisce subito che la risultante S delle azioni che si trasmettono attraverso pareti verticali come la AB, è parallela alle rette di massima pendenza del piano di campagna, e la sua grandezza non dipende dal particolare punto A, ma è la stessa in A′B′ e per ogni altra parete come AB. Inoltre, le azioni che si trasmettono lungo la parete di fondo BB′ (parallela al piano di campagna) devono essere verticali e pari al peso P del prisma di terra sovrastante. La corrispondente pressione è pari cioè a γth, con γt peso specifico della terra e h altezza del punto considerato sotto il piano di campagna. Per quanto riguarda l’inclinazione della S, essa forma un angolo ɛ con l’orizzontale, mentre, per quanto riguarda la grandezza della S, essa è certamente compresa tra due valori corrispondenti rispettivamente a una condizione di equilibrio limite inferiore e a una di equilibrio limite superiore o, come si suole anche dire, corrispondenti rispettivamente alla condizione di s. attiva (minimo valore della S compatibile con l’equilibrio) e alla condizione di s. passiva (massimo valore della S). La teoria di Rankine è valida per la determinazione della s. attiva, salvo le ulteriori precisazioni sull’applicabilità della teoria stessa nel campo delle strutture di sostegno (precisazioni dovute a C.O. Mohr e M. Lévy); va rilevato infatti che essa fornisce il valore delle azioni che si trasmettono attraverso una parete ideale (verticale o inclinata) all’interno del masso. Perché si possano assumere quegli stessi valori per le azioni trasmesse da un terrapieno a una struttura di sostegno, è necessario che la distribuzione degli sforzi resti inalterata all’interno del masso, nonostante l’eliminazione di una sua parte e la sua sostituzione con una struttura capace di mantenere in equilibrio la parte restante del masso.

Metodo della perdita o della caduta di s. (o della s. addizionale)

Metodo di calcolo impiegato per il progetto di archi iperstatici, a 2 cerniere o incastrati. L’asse dell’arco viene tracciato come linea funicolare delle forze esterne agenti sull’arco, e perciò l’arco risulterebbe tutto compresso se i vincoli consentissero liberamente la deformazione che compete alla sola sollecitazione di pressione. In effetti la presenza dei vincoli di estremità impedisce l’accorciamento che dovrebbe avere la corda dell’arco nella deformazione indotta dalla pressione. Ciò equivale, se l’arco in esame è incernierato alle estremità, a una riduzione di valore della componente orizzontale della s. rispetto al valore che essa avrebbe in un arco uguale, ma reso isostatico con l’aggiunta di una terza cerniera intermedia; analogamente, si avrebbe una riduzione della componente medesima qualora si rendesse isostatico un arco incastrato agli estremi, trasformando gli incastri in cerniere e aggiungendo sempre la terza cerniera. In questo secondo caso alla riduzione di s. orizzontale si accompagna anche il sorgere di un momento flettente nella sezione d’incastro, il cui valore è facilmente deducibile dalla caduta di s. quando si conosce il centro elastico dell’arco.