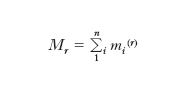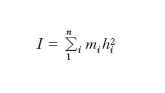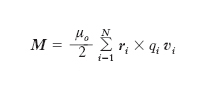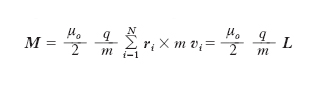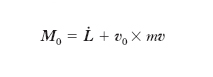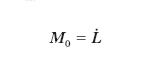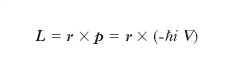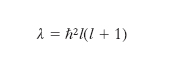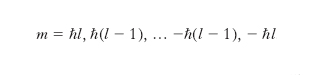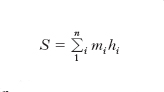momento

In fisica e tecnica, termine usato, con diverse specificazioni, per indicare varie grandezze, scalari o vettoriali, aventi in comune il fatto di poter essere definite come prodotto di una certa altra grandezza per una distanza (come nel caso del m. di una forza) o per il quadrato di una distanza (come nel m. d’inerzia). Per influsso della terminologia scientifica inglese e statunitense, il termine viene talora usato per indicare la quantità di moto.

M. di una forza rispetto a una retta e rispetto a un punto

fig. 1

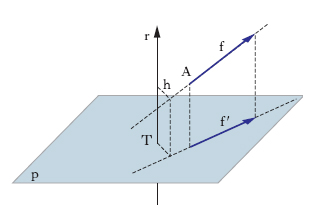
Una forza f sia applicata in un punto A e sia r una retta orientata. Per un punto qualunque T di r (fig. 1) si immagini condotto il piano π normale a r e sia f′ il componente normale della forza rispetto a r: si chiama m. di f rispetto a r, o m. assiale di f rispetto a r (asse) o anche m. scalare di f rispetto a r, il prodotto m_r del modulo di f′ per la distanza h tra la retta di applicazione di f e la retta r (h è il braccio della forza rispetto a r) preso col segno + o − a seconda che f (e quindi f′) sia levogiro o destrogiro rispetto a r: m_r=±hf′ (in fig., segno +). La definizione si generalizza in modo ovvio e immediato a un vettore applicato qualunque. Il m. assiale di un vettore si annulla soltanto se vettore e retta sono complanari (per incidenza: h=0; per parallelismo: f′=0). Se f è in un piano normale a r si ha semplicemente m_r=±hf: il m. è allora il prodotto (con segno) del modulo della forza per il suo braccio. Il trasporto di una forza o, genericamente, di un vettore applicato lungo la sua retta di applicazione non altera i m. assiali. Per un sistema di forze o di vettori applicati si definisce m. risultante assiale, o scalare, rispetto a una retta r, la somma algebrica dei momenti assiali dei singoli vettori:

fig. 2

Dati un punto O (fig. 2) e un vettore f (sia questo ancora, per es., una forza) applicato in un punto A, (A, f), si chiama m. polare (o m. vettoriale o semplicemente m.) di f rispetto a O (polo) il prodotto vettoriale m=OA×f. Si tratta di un vettore di modulo uguale al prodotto di f per la distanza h di O dalla retta di applicazione di f, di direzione normale al piano determinato dai due vettori OA e (A, f), di verso tale che la terna dei tre vettori, nell’ordine OA, (O, f), (O, m), risulti levogira. Se O si trova sulla retta di applicazione di (A, f), il m. è nullo; spostando f sulla sua retta di applicazione m non cambia. Il m. di un vettore applicato rispetto a un polo e il suo m. rispetto a un asse per il polo sono legati dalla proprietà che il secondo coincide con la componente del primo secondo l’asse considerato. Per un sistema di vettori applicati si chiama m. risultante polare, o semplicemente m. del sistema, rispetto a O, il risultante dei m. dei singoli vettori. Il m. M del sistema rispetto a un polo T è legato al m. M′ rispetto a un altro polo T′ dalla relazione M=M′+T T′×R, dove R è il risultante del sistema di vettori dato. Se R=0 si ha M=M′: il m. non dipende dalla scelta del polo. È questo il caso di una coppia di forze (o più genericamente di una coppia di vettori applicati), il cui m. polare, normale al piano della coppia, risulta uguale in modulo al prodotto dell’intensità di questa per il suo braccio: la proprietà di legame fra m. polari e m. assiali prima ricordata spiega perché il m. d’una coppia rispetto a un qualunque asse parallelo al suo piano è nullo, mentre rispetto a un qualunque asse normale è uguale al prodotto dell’intensità per il braccio.

M. flettente e m. torcente

fig. 3A

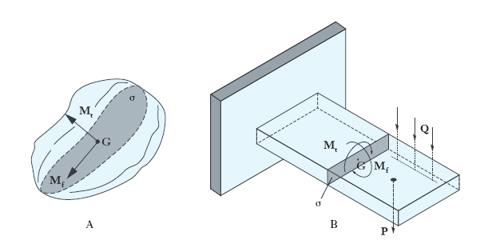
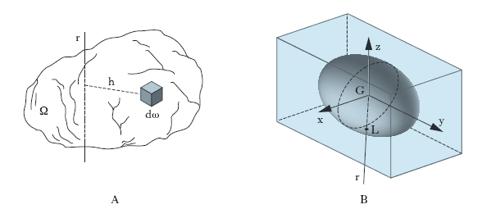
Tracciata una qualsiasi area piana σ all’interno di un generico solido continuo (fig. 3A), si definisce m. flettente sulla σ il componente tangenziale, rispetto alla giacitura di σ, del m. risultante, calcolato rispetto al centro di massa G di σ, delle forze molecolari che le particelle del solido poste da una parte di σ esplicano sulle particelle poste dall’altra parte. Il componente normale, rispetto a σ, del medesimo m. risultante ha invece il nome di m. torcente. Nel caso particolare dei solidi tubolari, e con riferimento a una generica sezione trasversale, come conseguenza delle equazioni cardinali della meccanica si riconosce che il m. flettente e il m. torcente sono rispettivamente uguali ai componenti tangenziale e normale del m. risultante rispetto a G delle eventuali forze d’inerzia e di tutte le forze esterne (di superficie e di massa) agenti sul tronco di solido compreso tra un’altra qualsiasi sezione, considerata di estremità e la sezione che si considera, ivi comprese le forze che si esercitano sulla sezione di estremità e che possono anche essere di natura molecolare. Nel caso statico (fig. 3B), che più direttamente interessa gli ordinari problemi di scienza delle costruzioni, manca naturalmente il contributo delle forze d’inerzia, sicché i m. flettente e torcente possono essere determinati operando sulle sole forze esterne. In altri termini, il m. flettente e il m. torcente relativi a una certa sezione σ del solido rappresentano lo stato di tensione interna indotto nel solido in corrispondenza a σ da una sollecitazione esterna capace di provocare rispettivamente flessione o torsione del solido.

M. d’inerzia

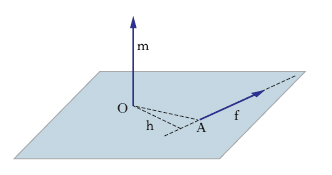
Per un insieme di n masse m₁, m₂, ..., m_i, ..., m_n, concentrate in altrettanti punti P₁, P₂, ..., P_i, ..., P_n, si dice m. d’inerzia rispetto a una retta r la somma I dei prodotti delle masse per i quadrati delle rispettive distanze da r:

fig. 4A

Per un sistema continuo Ω (fig. 4A), detta μ la densità e h la distanza da r del generico elemento (volumico, areico, o lineico) dω del sistema, si definisce m. d’inerzia rispetto a r l’integrale I=∫_Ωμh²dω. Le dimensioni fisiche di un m. d’inerzia sono in ogni caso quelle del prodotto d’una massa per il quadrato d’una lunghezza. I m. d’inerzia intervengono nella dinamica dei solidi rotanti, nella scienza delle costruzioni ecc. A fondamento della teoria sono due teoremi: il primo, noto come teorema di Huygens, stabilisce che il m. d’inerzia I di un sistema materiale Ω rispetto a una retta r è uguale al m. d’inerzia I_o del sistema rispetto alla parallela a r condotta per il centro di massa di Ω, aumentato del prodotto della massa totale m del sistema per il quadrato della distanza d fra le due rette: I=I₀+md². Il teorema di Huygens fissa in definitiva come varia il m. d’inerzia spostando la retta, cui esso si riferisce, parallelamente a sé stessa. Il secondo teorema stabilisce invece che, se si fa ruotare la retta intorno a un suo punto O, il m. varia secondo la legge

I=Aα²+Bβ²+Cγ²−2A′βγ−2B′γα−2C′αβ

essendo A, B, C i m. d’inerzia di Ω rispetto agli assi di riferimento x, y, z (scelti comunque ma con l’origine in O) e α, β, γ i coseni direttori rispetto ai medesimi assi della retta per O cui si riferisce I; A′, B′, C′ sono i cosiddetti prodotti d’inerzia o m. di deviazione.

Un’efficace rappresentazione geometrica del modo di variare del m. d’inerzia rispetto ad assi concorrenti in un punto si ha nell’ellissoide d’inerzia. Si pensi riportato sulla generica retta r per O, da una parte e dall’altra di O, un segmento OL=1/√‾‾I (ove I è il m. d’inerzia di Ω rispetto a r); al ruotare della retta attorno a O, l’estremo L del segmento OL descrive un ellissoide che si chiama appunto ellissoide d’inerzia relativo a O. Variando O l’ellissoide in generale varia, sicché per ogni sistema materiale esistono ∞³ ellissoidi d’inerzia (cioè tanti quanti sono i punti dello spazio). Gli assi dell’ellissoide relativo a O si dicono assi principali d’inerzia relativi a O; i m. d’inerzia rispetto a essi m. principali d’inerzia. Scegliendo gli assi principali d’inerzia come assi di riferimento si hanno notevoli semplificazioni per l’annullarsi dei prodotti d’inerzia A′, B′, C′. L’ellissoide d’inerzia relativo al centro di massa si dice ellissoide centrale d’inerzia (fig. 4B); i suoi assi si chiamano assi centrali d’inerzia; i m. rispetto a essi, m. centrali d’inerzia. Ove intervengano particolari condizioni di simmetria nella distribuzione delle masse intorno a O, il corrispondente ellissoide d’inerzia può ridursi a un ellissoide di rotazione o addirittura a una sfera. Se l’ellissoide centrale d’inerzia di un solido è rotondo, il solido si dice a struttura giroscopica; ciò si verifica di certo per ogni solido omogeneo di rotazione, il cui ellissoide centrale è rotondo intorno all’asse di rotazione del solido medesimo (giroscopio in senso stretto).

La ricerca, per un dato sistema materiale, degli assi principali relativi a un punto, e in particolare quella degli assi centrali, ha un’importanza notevole sia in problemi statici sia in dinamica. Essa riesce molto facilitata quando il sistema ammetta piani di simmetria ortogonale, e ciò per il fatto che la normale in un suo punto O a un tale piano di simmetria è uno degli assi principali d’inerzia relativi a O. Un sistema piano in particolare ammette sempre un piano, quello π in cui giace il sistema, che può considerarsi di simmetria. Poiché anche il centro di massa G appartiene in tal caso a π, uno degli assi centrali è sempre la normale per G a π.

M. magnetico (o m. di dipolo magnetico)

Per un sistema di N particelle, con masse mi, cariche qi, in moto con velocità vi (i=1,2, ..., N) in una regione limitata di spazio, il m. magnetico M è definito come

essendo r_i il raggio vettore della i-ma particella e μ_o la permeabilità magnetica assoluta del vuoto. Se il rapporto tra carica e massa è lo stesso per tutte le particelle (q_i/m_i=q/m), oppure se si considera una sola particella (di carica q e massa m) si ha:

cioè il m. magnetico è proporzionale al m. della quantità di moto.

M. della quantità di moto (o m. angolare) Grandezza di particolare rilievo in meccanica, in quanto a essa è legato uno dei teoremi fondamentali della dinamica (teorema del m. della quantità di moto ➔ dinamica). In particolare, per un punto materiale P in moto, di massa m, velocità v, il m. suddetto, rispetto a un polo O vale L=OP×mv, e il teorema ora ricordato si esprime nella relazione

dove M₀ è il momento rispetto a O, della forza totale F agente su P, L̇ il derivato di L rispetto al tempo, v₀ la velocità di O. Se O è un punto fisso, com’è il caso quando esso coincide con l’origine della terna (fissa) di riferimento, la relazione precedente si riduce a

se, più in particolare, è M₀=0, si ricava che dev’essere L=cost: relazione nota come integrale (primo) del m. della quantità di moto e che esprime la conservazione del m. della quantità di moto.

In meccanica quantistica il m. angolare, come ogni variabile dinamica, è rappresentato da un operatore. Nella rappresentazione delle coordinate, alla variabile quantità di moto p è associato l’operatore -ℏi ∇ (dove ℏ è la costante di Planck divisa per 2π e i è l’unità immaginaria) e il m. angolare si scrive, per una particella,

formula [1] .

La variabile L risulta quantizzata; in particolare: a) il modulo quadro del m. angolare può assumere i valori

,

con l = 0, 1, 2, ...; b) i valori possibili per ognuna delle componenti di L in uno stato in cui L² ha valore ℏ²l(l + 1) sono

.

I valori seminteri di l, che non sono ammissibili per l’operatore L definito nella [1] (chiamato anche m. angolare orbitale), sono invece permessi, insieme ai valori interi, per l’eventuale m. angolare intrinseco, o di spin della particella, che indicheremo con S. Tale m. angolare intrinseco, la cui esistenza ha solide basi sperimentali, è indipendente dalle variabili r, p, che descrivono il moto traslatorio della particella nello spazio, ma si riferisce a gradi di libertà interni (o di spin). Il m. angolare totale di una particella con spin diverso da zero è dunque J=L+S.

M. resistente

Nella scienza delle costruzioni, grandezza caratteristica della generica sezione trasversale di una trave soggetta a flessione semplice o a flessione e taglio, quando si adotti per il calcolo il metodo delle tensioni ammissibili. È definita dal prodotto del carico di sicurezza del materiale di cui è costituita la trave per il modulo di resistenza della sezione considerata. Esso rappresenta pertanto il massimo valore del m. flettente cui può essere assoggettata la trave nella sezione in esame, subordinatamente alla condizione che la tensione normale non superi il valore del carico di sicurezza.

Per un corpo in rotazione soggetto a forze resistenti, si chiama m. resistente il m. risultante di queste rispetto all’asse di rotazione. Al m. resistente si contrappone il m. motore che per un corpo in rotazione è il m. risultante dalle forze motrici rispetto all’asse di rotazione del corpo.

M. statico

Per un punto materiale P di massa m, si chiama m. statico, rispetto a un assegnato piano π, il prodotto di m per la distanza h di P da π presa, convenzionalmente, col segno + o − a seconda che P si trovi da una parte o dall’altra di π. La definizione si estende in modo ovvio ai sistemi. Per un sistema discreto il m. statico è la somma algebrica,

dei m. statici dei singoli punti; per un sistema continuo Ω è l’integrale esteso a Ω, ʃ_Ωμhdω, del m. statico elementare (μ densità, dω elemento del corpo, μdω massa elementare, h sua distanza con segno dal piano).

Secondo la regola dei m. statici, il m. statico di un sistema rispetto a un qualsiasi piano α coincide col m. statico rispetto ad α della massa totale concentrata nel baricentro. La regola, oltre che al più semplice calcolo di m. statici, può servire alla determinazione del baricentro. Anziché rispetto a piani si possono considerare, con analoga definizione, i m. statici rispetto a rette: anzi, per un sistema materiale piano generalmente ciò che interessa sono precisamente i suoi m. statici rispetto a rette del piano. L’intervento dei m. statici è sistematico in molte questioni attinenti alla scienza delle costruzioni.