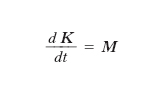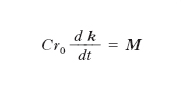giroscopio

fig. 1

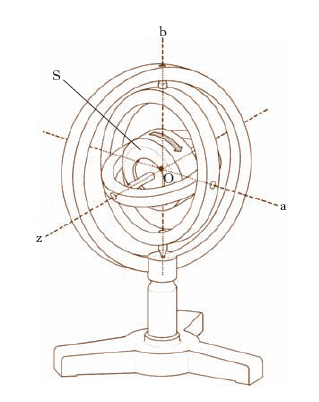
Solido con ellissoide centrale d’inerzia di rotazione intorno a un determinato asse (asse giroscopico), capace di essere posto in rotazione intorno a tale asse, il cui assetto nello spazio, grazie a un supporto cardanico, può essere qualunque. Nel g. semplice, o di Foucault (fig. 1) il solido in questione S è un disco omogeneo piuttosto massiccio. Posto che sia il disco in rapida rotazione (mediante vari artifici: a mano, svolgendo rapidamente una funicella avvolta sull’asse del disco, per finire a dispositivi ad aria compressa o elettromagnetici), il suo asse z, comunque si muova il supporto, resta sempre puntato, finché duri la rotazione, nella direzione iniziale, cioè in posizione immutabile rispetto alle stelle fisse (cosiddetta permanenza dell’asse giroscopico). Ciò per un g. libero, nel quale il momento della quantità di moto di rotazione è esattamente diretto lungo l’asse giroscopico; se, però, interviene una qualche forza esterna che fa insorgere un componente del detto momento in direzione trasversale all’asse, insorge un moto di precessione intorno all’asse (effetto giroscopico). Le accennate proprietà del g. danno luogo a una serie di importanti applicazioni, sia per determinare direzioni, come, per es., nelle bussole giroscopiche e nelle piattaforme inerziali, sia per stabilizzare movimenti di altri corpi, come, per es., negli stabilizzatori giroscopici delle navi.

Formulazione matematica

In base alla seconda equazione cardinale della dinamica dei sistemi di punti materiali, per un generico solido S in moto, indicando con K il momento risultante delle quantità di moto rispetto a un assegnato polo O, con M il momento risultante, sempre rispetto a O, delle forze esterne agenti su S, si scrive, se O è un punto fisso o coincide istante per istante con il centro di massa di S,

[1] formula,

essendo t il tempo, e in tali ipotesi per K vale l’espressione

[2] K = A p i + B q j + C r k,

essendo i, j, k i versori degli assi principali d’inerzia relativi a O assunti come assi x, y, z del riferimento solidale a S; A, B, C i corrispondenti momenti principali d’inerzia; p, q, r le componenti, secondo i medesimi assi, della velocità angolare ω da cui S è animato nel suo moto rispetto al riferimento fisso. Si supponga ora che S sia un g. fissato in un punto O dell’asse giroscopico z (fig. 1) e che a S venga impressa una forte velocità giroscopica, in modo che inizialmente ω risulti diretta secondo z, e il suo valore iniziale ω₀ sia quindi esprimibile nella forma ω₀ = r₀k. Se, inoltre, si verifica la circostanza che M sia nullo oppure normale all’asse giroscopico z, dalla [1] si trae che durante il moto la componente r di ω secondo z conserva sempre il valore r₀ che aveva inizialmente. Durante il moto, a rigore, r non è, come all’istante iniziale, l’unica componente di ω diversa da zero; ma se si spinge un pò più oltre l’analisi si riconosce che, se r₀ è molto grande, ciò si può ammettere con soddisfacente approssimazione almeno per un certo intervallo di tempo a partire dall’istante iniziale, e di conseguenza, a norma della [2], si può assumere per K l’espressione, approssimata,

[3] K = Cr₀k.

Nell’ammettere la validità della [3] consiste quello che si chiama il principio dell’effetto giroscopico. In conseguenza della [3], stante la costanza di C e di r₀, la [1] diventa

[4] formula,

fig. 2

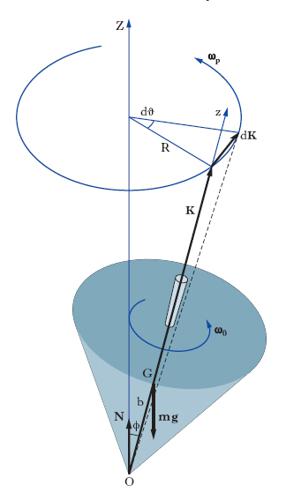
e il principio suddetto si può enunciare dicendo che i moti di S corrispondenti a una stessa posizione iniziale hanno, per r₀→∞, uno stesso comportamento asintotico definito dalla [4]. È in base a quanto detto che si può spiegare, per es., il comportamento di una trottola. Consideriamo una trottola che ruoti intorno al suo asse di simmetria con velocità angolare ω₀ (fig. 2). Il momento risultante delle forze (forza peso mg e reazione del piano di appoggio N) rispetto al punto di appoggio O della trottola è perpendicolare a K e in modulo vale M=mgb sen ϕ, essendo ϕ l’angolo compreso tra l’asse di simmetria z e l’asse verticale Z, e b la distanza del centro di massa G da O. In un piccolo intervallo di tempo il vettore K subisce una variazione dK=Mdt parallela a M. L’estremo libero del vettore K descrive una circonferenza, intorno all’asse Z, di raggio pari a R=K sen ϕ. La velocità angolare di precessione con la quale l’asse z della trottola ruota intorno all’asse Z (del riferimento fisso) è data da ω_p=dϑ/dt. Si ha pertanto dK=Rdϑ=K sen ϕ∙ω_pdt e quindi ω_p=M/K sen ϕ=mgb/Cr₀, nell’approssimazione K≃Cr₀k. Uno studio più approfondito mostra che in generale l’angolo ϕ non rimane costante ma oscilla tra due valori fissi, cioè l’asse della trottola compie delle oscillazioni (nutazione). Si può osservare che in ogni tempuscolo dt lo spostamento dk dell’estremo libero del vettore k applicato in O è, come risulta dalla [4], parallelo a M; questo fatto è ricordato come principio della tendenza al parallelismo dell’asse giroscopico al momento sollecitante. La grandezza dello stesso dk risulta poi, a parità di M e di C, tanto minore quanto maggiore è la velocità giroscopica r₀: principio della permanenza, o tenacia, degli assi giroscopici.

Altri dispositivi giroscopici

Accanto al g. comune altri semplici dispositivi giroscopici sono: il barogiroscopio e la bussola giroscopica, ambedue costituiti da un g. S il cui asse, oltre a essere fissato in un suo punto O, è vincolato, sempre senza sensibile attrito, a non uscire da un piano fisso alla Terra: nella bussola, O coincide col baricentro di S; nel barogiroscopio ne è distinto.

Gli effetti giroscopici vengono sfruttati per la stabilizzazione dei proiettili sulla traiettoria, nell’orizzonte artificiale, negli indicatori di virata, nei girostabilizzatori per navi ecc.

fig. 3

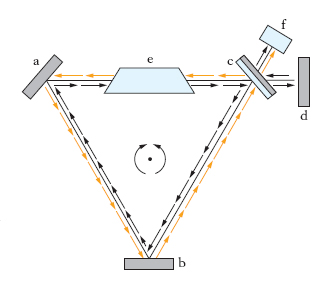
G. a laser Dispositivo costituito da un laser, la cui cavità ottica è il percorso chiuso triangolare indicato in fig. 3, realizzato mediante due specchi ordinari a, b, e uno specchio c parzialmente riflettente, dal quale si estraggono, mediante un altro specchio d disposto come indicato, i due sistemi di onde che, emessi dal materiale attivo e, procedono in versi opposti lungo il percorso anzidetto e interferiscono poi tra loro in un rivelatore fotoelettrico f; se il sistema ruota intorno a un asse ortogonale al piano del cammino e passante per il centro di questo, in virtù dell’effetto Doppler le frequenze dei due sistemi di onde variano, e ne risulta, nel rivelatore, una frequenza di battimento. Sullo stesso principio si basa il funzionamento dei g. a fibre ottiche, in cui i due sistemi di onde, emessi da un diodo laser, percorrono in senso inverso un lungo tratto di fibra chiuso su se stesso. L’insieme di tre dispositivi di questo genere, con cammini su piani mutuamente ortogonali, è in grado di evidenziare rotazioni rispetto a un riferimento inerziale, giustificando così la denominazione data al dispositivo.