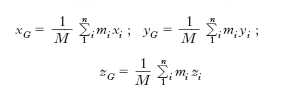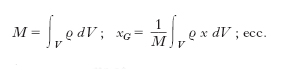baricentro

Centro di gravità di un insieme discreto di n masse m₁, m₂, ... m_i ,... m_n, concentrate in altrettanti punti P₁, P₂, ... P_i, ... P_n, coincidente col centro di un sistema di n vettori paralleli e concordi di lunghezze proporzionali alle masse, di orientamento arbitrario, applicati nei medesimi punti. Il b. coincide pertanto con il centro del sistema dei vettori peso dei singoli punti materiali, se si ipotizza che nei singoli punti il vettore g dell’accelerazione di gravità sia il medesimo. La definizione si può utilizzare per determinare, graficamente, il b. di un insieme piano di masse (➔ centro). Fissata una terna di riferimento, indicate con x_i, y_i, z_i le coordinate di P _i, con M la massa totale, cioè la somma di tutte le masse del sistema, le coordinate del baricentro G sono date da

Se, anziché con un sistema discreto, si ha a che fare con un sistema continuo S, valgono formule analoghe che si ottengono dalle precedenti sostituendo la massa elementare ρdV (ρ densità, dV elemento del sistema) alla massa concentrata m_i e gli integrali alle sommatorie. Si ha cioè per un sistema continuo:

Se poi il sistema continuo è omogeneo, ρ è costante e nelle formule che danno le coordinate di G essa si elimina fra numeratore e denominatore, sicché G viene a presentarsi come una caratteristica puramente geometrica del corpo e si può parlare del b. di un triangolo, di una sfera, di un cono ecc., senza precisare di quale sostanza il corpo sia costituito.

determinazione

La determinazione di un b. può essere immediata, o almeno risultare facilitata, applicando opportunamente le proprietà di simmetria e distributiva; per la prima, se un sistema ammette un centro, un asse o un piano di simmetria, il b. coincide col centro o sta sull’asse o sul piano di simmetria; per la seconda, se si divide un sistema in parti e di ciascuna di queste si determinano la massa e il b., il b. dell’intero sistema coincide con quello dei b. dei punti rappresentativi delle singole parti caricati ciascuno delle masse delle parti stesse. In virtù di queste proprietà si può subito dire, per es., che i b. di una sfera, di un cerchio, di un quadrato omogenei, cadono nei rispettivi centri geometrici; che il b. di un triangolo omogeneo è il punto d’incontro delle mediane.