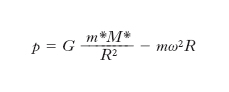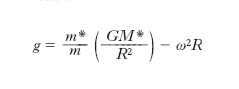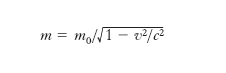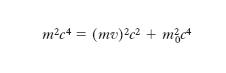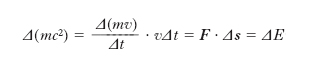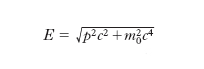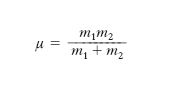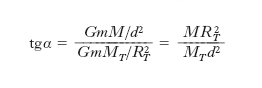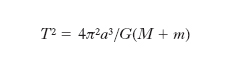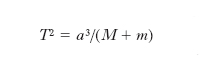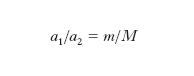massa

Fisica

Secondo la definizione introdotta da Newton, e spesso ancora usata, la m. è la quantità di materia contenuta in un corpo. Questa definizione non ha però un significato preciso in quanto non è basata su criteri operativi che ne fissano una procedura di misurazione. Il concetto di m. si precisa invece tramite la legge fondamentale della dinamica (il secondo principio della dinamica, enunciato dallo stesso Newton) come il rapporto (invariabile) fra la forza applicata a un corpo e l’accelerazione che ne consegue (in un sistema di riferimento inerziale).

M. inerziale e gravitazionale

A parità di forza un corpo subisce, nello stesso intervallo di tempo, una variazione di velocità tanto più piccola quanto più grande è la sua m.: quindi questa misura l’inerzia del corpo a rispondere alla forza che lo sollecita e per questo viene detta m. inerziale.

Si osserva sperimentalmente che in un dato luogo tutti i corpi sono attratti dalla Terra in ragione diretta della loro m. inerziale, cioè che l’intensità della forza peso è proporzionale alla m. inerziale con costante di proporzionalità (accelerazione di gravità) uguale per tutti i corpi: ciò sta a indicare che, entro i limiti di precisione sperimentali, la grandezza fisica responsabile della forza peso di un corpo, cioè la sua m. gravitazionale che interviene nell’espressione della forza di gravitazione universale, è proporzionale alla m. inerziale, di modo che facendo coincidere il campione di m. inerziale con il campione di m. gravitazionale il loro valore numerico si può far coincidere. Indicando infatti con m la m. inerziale di un corpo posto sulla superficie terrestre all’equatore (ma il discorso è facilmente generalizzabile a qualsiasi latitudine), con m* la sua m. gravitazionale, la legge sperimentale della proporzionalità tra intensità della forza peso p e m. inerziale può scriversi p=mg dove g è una costante che ha nello stesso luogo lo stesso valore per tutti i corpi; ma in termini di gravitazione universale l’intensità della forza peso può anche scriversi, tenendo conto del moto di rotazione della Terra,

,

dove G è la costante di gravitazione universale, M* la m. gravitazionale, R il raggio e ω la velocità angolare della Terra; uguagliando le due espressioni ottenute per p si ha

e poiché sperimentalmente g è lo stesso per tutti i corpi, discende che il rapporto m*/m deve avere lo stesso valore per tutti i corpi, cioè la m. gravitazionale è proporzionale alla m. inerziale. L’identità della m. inerziale e della m. gravitazionale costituisce una delle leggi fondamentali della relatività generale (➔ gravitazione e relatività).

M. relativistica

Nella meccanica classica viene postulata l’assoluta invariabilità della m. e in particolare la sua indipendenza dalle condizioni di moto del corpo, ciò che non è più vero per corpi in moto con velocità confrontabili con la velocità della luce per i quali bisogna far ricorso alla meccanica relativistica. Se m₀ è la m. a riposo (o di quiete) di un corpo, cioè la sua m. in condizioni di quiete, la m. m dello stesso corpo alla velocità v, detta anche m. relativistica, vale

,

fig. 1

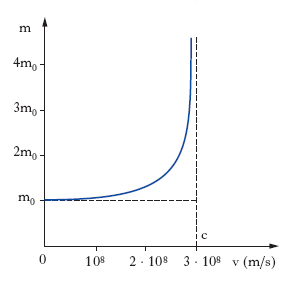
essendo c la velocità delle onde elettromagnetiche nel vuoto (ca. 3∙10⁸ m/s): la m. relativistica è sempre maggiore della m. a riposo, ma se la velocità del corpo è molto piccola rispetto alla velocità c, il rapporto v²/c² diventa trascurabile rispetto all’unità e con esso diventa trascurabile la correzione relativistica in modo da potersi ammettere, senza sensibile errore, che sia m=m₀ (fig. 1). È questo uno dei motivi per i quali, malgrado l’avvento della meccanica relativistica, la meccanica classica non ha perso la sua primitiva importanza nei confronti delle sue ordinarie applicazioni. Viceversa, per velocità dell’ordine di grandezza di c, la m. relativistica assume valori estremamente elevati (come è stato provato sperimentalmente dallo studio delle particelle elementari), divergendo quando v tende a c.

Dall’espressione della m. relativistica discende

[1] formula

e anche

quindi l’energia E di un corpo è data da

E = mc²

o anche da

Ponendo p=mv, la [1] fornisce inoltre

pertanto a un corpo fermo (v=0) è in particolare associata una energia

E₀=m₀c²,

connessa alla sua m. a riposo m₀. In definitiva, a ogni forma di energia è associata una m. (inerziale e gravitazionale) e a ogni m. (anche in quiete) un’energia, come è ampiamente verificato sperimentalmente; la m. è convertibile in energia e l’energia in m. secondo il rapporto di conversione c² (che esprime l’energia equivalente all’unità di m.), cioè m. ed energia sono equivalenti.

Misura della massa

Le varie grandezze dinamiche non possono essere espresse, come quelle cinematiche, in funzione soltanto di lunghezza e di tempo, le due grandezze abitualmente assunte come fondamentali nella cinematica. A queste occorre associare in dinamica o la m. o la forza; non tutte e due, perché esse, legate dalla relazione F=ma, non sono fra loro indipendenti. Quando alla lunghezza e al tempo si associa la m., il sistema di unità di misura che ne consegue si dice assoluto. Naturalmente, la scelta dell’unità di m. è in tal caso libera, mentre resta determinata l’unità di forza, che è allora grandezza derivata. Sistemi assoluti sono il sistema CGS, in cui l’unità di m. è il grammo (g), il sistema MKS e il Sistema Internazionale (SI), in cui l’unità di m. è il kilogrammo (kg). Accanto al kilogrammo e al grammo altre unità possono naturalmente essere usate per la misura delle m., e difatti lo sono sia nei paesi dove il Sistema Internazionale non è ancora entrato completamente nell’uso (per es., la libbra nei paesi anglosassoni) sia in particolari settori tecnici e scientifici (per es., l’unità di m. atomica in fisica e in chimica).

tab.

La m. viene correntemente misurata mediante le bilance. La m. degli atomi ionizzati e delle particelle subatomiche cariche viene generalmente determinata misurando la curvatura 1/R della traiettoria delle stesse in moto in un campo magnetico: 1/R=qB/mv (dove q è la carica elettrica e v la velocità della particella, B il modulo del vettore induzione magnetica). Per le particelle neutre si ricorre allo studio di processi (per es., collisioni, decadimenti ecc.) nei quali siano note le m. di tutte le particelle in gioco eccetto una: la m. incognita è determinata misurando le quantità cinematiche coinvolte nel processo e utilizzando la conservazione della quantità di moto e dell’energia. Nella tab. sono riportati i valori, per lo più puramente indicativi, di alcune masse.

M. atomica

La m. atomica di un elemento è la m. a riposo di un atomo di quell’elemento; correntemente, ma non propriamente, è detta anche peso atomico, tale uso è particolarmente seguito nella chimica. Le m. atomiche sono espresse di solito, anziché in kg o in g, in unità di m. atomica (simbolo u) definita come la dodicesima parte della m. del più importante e abbondante isotopo naturale del carbonio, il ¹²C. L’unità di m. atomica, uguale a 1,6605655∙10⁻²⁷ kg, è entrata a far parte del Sistema Internazionale come unità definita indipendentemente dalle sette unità di base. Nelle questioni di fisica nucleare e subnucleare è usuale esprimere la m. di corpuscoli in MeV/c² o anche talvolta per l’equivalenza m.-energia (E=mc²) in unità di energia; l’unità di m. atomica vale 931,554 MeV/c².

M. efficace (o effettiva)

Grandezza che va sostituita alla m. reale di un corpo, quando le proprietà inerziali di esso vengono apparentemente modificate dalla sua interazione con altri corpi o in generale con l’ambiente circostante. Così, s’introduce il concetto di m. efficace nella trattazione del moto di un corpo in un fluido, o dei moti degli elettroni in un solido conduttore. Nel caso specifico degli elettroni di conduzione nei metalli e nei semiconduttori, la trattazione quantistica del fenomeno porta alla conclusione che la m. effettiva è suscettibile di variare a seconda del livello energetico in cui si trovano gli elettroni medesimi, potendo in particolare assumere anche valori negativi.

M. ridotta

La m. ridotta è la quantità usata nelle questioni di meccanica riducibili allo schema del problema dei due corpi (➔ corpo), quali quelle relative ad astri con un satellite, all’atomo di idrogeno, ai sistemi idrogenoidi. In genere, per trovare l’orbita del corpo di m. minore, m₁, si suppone che l’altro corpo abbia una m. m₂ molto maggiore di m₁ e che perciò rimanga immobile; tale ipotesi molto spesso non corrisponde alla realtà. Si dimostra che i risultati trovati con quella ipotesi molto limitativa valgono ancora purché la m. m₁ sia sostituita con la m. ridotta

Si vede che per m₂ tendente a ∞, e cioè quando il baricentro del sistema coincide praticamente con quello del solo corpo di m. m₂, μ tende a m₁.

Astronomia

M. della Terra

fig. 2.

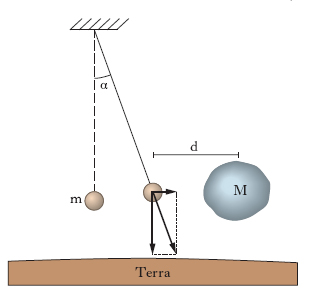
La Terra è stato il primo corpo celeste di cui si sia riusciti a determinare la massa. Le prime determinazioni vennero effettuate da P. Bouguer e C.-M. La Condamine intorno al 1740 e da N. Maskelyne intorno al 1770 con il metodo, in precedenza proposto da Newton, illustrato in fig. 2. Un pendolo di m. m è soggetto sia alla attrazione della Terra (di m. M_T) sia a quella di un corpo (di m. M), disposto lateralmente. Per la legge di gravitazione universale, se G è la costante di gravitazione, la prima forza ha intensità GmM_T/R²_T (dove R_T è il raggio della Terra) e la seconda GmM/d² (dove d è la distanza di m da M). Il pendolo, pertanto, si disporrà nella direzione indicata in figura, deviando dalla verticale di un angolo α, tale che:

Conoscendo M, d e R_T, si ricava M_T. Nell’esperimento di Maskelyne, la m. M era costituita da una montagna isolata (il Monte Shehallien in Scozia). Il valore di M_T ottenuto da Maskelyne (5,2∙10²⁴ kg) era sottostimato di circa il 13%. Misure più accurate della m. terrestre cominciarono a ottenersi quando H. Cavendish (1798) determinò il valore della costante di gravitazione G. Infatti, se questa è nota, si può ricavare M_T, misurando l’accelerazione di gravità g, dalla formula:

g=GM_T/R²_T

La precisazione della misura di M_T, ricavata con questo metodo, migliorò man mano che venne perfezionata quella della costante di gravitazione. Nel 1928, P.R. Heyl ottenne M_T=6∙10²⁴ kg, un valore assai vicino a quello oggi accettato (5,98∙10²⁴ kg).

M. dei corpi del sistema solare

La misura della m. di un pianeta è assai semplice, se intorno a esso orbita un satellite di m. relativamente piccola; infatti, se M è la m. del pianeta e m quella del satellite, la terza legge di Keplero può scriversi:

[1] formula,

dove T è il periodo di rivoluzione del satellite e a il semiasse maggiore della sua orbita. Misurando T e a e trascurando m (poiché si assume m≪M), dalla [1] si ricava M. Nel passato, con questa tecnica vennero determinate le m. di Marte, Giove, Saturno, Urano e Nettuno (tutti pianeti dotati di satelliti naturali). In modo analogo, applicando la [1] ai sistemi Terra-Luna e Sole-Terra, e utilizzando il valore noto della m. della Terra, vennero determinate la m. della Luna e quella del Sole. Queste misure sono state raffinate, utilizzando i satelliti artificiali: questi, rispetto ai satelliti naturali, offrono il duplice vantaggio di avere una m. del tutto trascurabile e di poter essere ‘tracciati’ con elevatissima precisione.

M. stellari

Misure dirette delle m. stellari sono possibili soltanto per le componenti di sistemi binari (➔ stella). Le misure più precise si ottengono per le binarie visuali (cioè le stelle doppie risolvibili al telescopio). Misurando la separazione angolare dei due astri, e conoscendo la distanza del sistema, si determina il semiasse maggiore (a) dell’orbita ellittica che la componente meno luminosa (‘secondaria’) descrive intorno a quella più brillante (‘primaria’). La terza legge di Keplero si può scrivere nella forma:

[2] formula,

dove M e m rappresentano le m., rispettivamente, della componente primaria e della secondaria, espresse in m. solari (M_⊙=1,99∙10³⁰ kg); T il periodo, misurato in anni; a il semiasse maggiore dell’orbita, misurato in unità astronomiche. Dalla [2] si ricava la m. totale del sistema (M+m). Occorre però tenere presente che quella che si osserva è l’orbita ‘apparente’, cioè la proiezione dell’orbita su un piano perpendicolare alla linea di vista. L’orbita ‘reale’ può essere calcolata misurando la distanza della componente primaria dal fuoco dell’orbita apparente (infatti, per la prima legge di Keplero, la componente primaria deve trovarsi proprio nel fuoco dell’orbita reale). La m. delle singole componenti può poi essere determinata se si riesce a osservare il moto di ciascuna di esse rispetto alle stelle di sfondo. In questo caso si può risalire al ‘moto orbitale assoluto’ dei due astri, cioè alle orbite che ciascuno di essi descrive intorno al centro di m. del sistema. Dalla definizione di centro di m. segue la relazione:

[3] formula,

dove a₁ e a₂ sono i semiassi maggiori delle orbite, rispettivamente, della componente primaria e di quella secondaria. Combinando la [2] e la [3], si ottengono M e m. Misure dirette di m. sono possibili per un numero limitato di stelle. È possibile, però, inferire la m. di molte altre, misurandone la luminosità (cioè la quantità di energia che esse irradiano nell’unità di tempo). Infatti, m. e luminosità di una stella sono legate fra loro dalla cosiddetta relazione m.-luminosità (➔ stella), che permette di determinare una delle due grandezze quando sia nota l’altra.

Per la misura delle m. delle galassie ➔ galassia.

M. mancante

In astrofisica, m. non osservata la cui esistenza è suggerita dalla dinamica di rotazione delle galassie a spirale e degli ammassi di galassie (nei quali la m. degli oggetti ‘visibili’, cioè che emettono radiazioni elettromagnetiche rilevabili dalla Terra, non è sufficiente a giustificare le velocità rispetto al centro di m. delle singole componenti del sistema). Il problema della m. mancante ha portato a ipotizzare l’esistenza di una forma di materia oscura (➔ materia) diffusa nell’Universo, che rivela indirettamente la sua presenza interagendo gravitazionalmente con la materia visibile.

Geologia

M. fondamentale Nei carboni fossili, m. amorfa, omogenea, colloidale, formatasi per coagulazione di sostanze vegetali decomposte in acqua, che ingloba frammenti di tessuto legnoso, cuticule di foglie, macro- e microspore, corpi resinosi ecc., talvolta sostanze minerali (calcite, pirite ecc.). È anche chiamata gelo fondamentale, gelo bruno-umico, materia fondamentale, sostanza fondamentale, substrato fondamentale.

Nelle rocce effusive o ipoabissali la m. fondamentale indica l’insieme (cristallino o vetroso) di quei componenti che rappresentano generazioni tardive rispetto ai fenocristalli. Nei confronti di questi, l’insieme risulta chimicamente differenziato denunciando un’evoluzione magmatica in senso acido. L’esame al microscopio di un consolidato effusivo, con riferimento alla sua m. fondamentale, permette, altresì, di distinguere termini di genesi intratellurica da termini d’ambiente subaereo o subacqueo.

Medicina

In anatomia, m. cerebrale, insieme dei tessuti nervosi contenuti nella scatola cranica; m. corporea, quantità totale di materia che costituisce il corpo; m. sanguigna, quantità totale di sangue di un organismo. In medicina, m. cristalline, residui del nucleo del cristallino che si rigonfiano in seguito a evento traumatico sul bulbo oculare o a intervento chirurgico per cateratta; m. neoplastica, insieme dei tessuti andati incontro a degenerazione neoplastica, localizzati in zone delimitate di organi.

Meteorologia

M. d’aria Porzione, generalmente abbastanza estesa, di aria che, per aver stazionato piuttosto a lungo sopra una regione terrestre avente caratteri fisici e geografici uniformi (oceano, continente esteso ecc.), acquista proprietà fisiche (temperatura e umidità) dipendenti dai caratteri della regione stessa. Se la m. d’aria così costituitasi si sposta su altre regioni, vi determina condizioni meteorologiche caratteristiche che dipendono dalle sue proprietà fisiche originali e dalle modificazioni successive da essa subite nel suo spostamento. Quindi ai cambiamenti delle m. d’aria conseguono di solito notevoli cambiamenti del tempo.

Se due m. d’aria diverse, per es. una calda di origine tropicale e una fredda proveniente da latitudini superiori, si incontrano, almeno in un primo tempo esse non si mescolano ma rimangono separate tra loro. Alle superfici di discontinuità che ne risultano (superfici frontali) sono connesse le maggiori perturbazioni atmosferiche.

Scienze sociali

Generalità

Di uso frequente nelle scienze sociali, il termine m. presenta significati ambigui o generici. Per quanto riguarda i suoi contenuti esistono almeno due referenti soggettivi: il proletariato come classe generale, perché incarna gli interessi della stragrande maggioranza della società, secondo quello che era il punto di vista prevalente delle teorie marxiste, e il ceto medio, cioè l’insieme dei gruppi che occupano le posizioni centrali nella piramide sociale, in quanto categoria residuale ma certamente assai estesa nei sistemi industriali. In ogni caso, le caratteristiche invarianti del concetto fanno riferimento a due dimensioni: una quantitativa, per cui la m. costituisce la base numericamente più ampia della società (‘i molti’ di cui parlava già Aristotele nella sua tipologia sulle forme di governo); l’altra qualitativa, per cui la m. definisce una collettività ‘emergente’ di individui, tale cioè da non poter essere ridotta alla loro somma, accomunati da qualche elemento per lo più oggettivo (lo stato di subalternità politica, la somiglianza degli stili di vita, la prossimità fisica o emotiva ecc.).

Nella tradizione degli studi sociologici si possono distinguere ancora due tendenze di massima. Da una parte, la tendenza a considerare, in negativo, la m. come un prodotto del processo di spersonalizzazione dell’individuo in collettività indistinte: in questo senso il concetto di m. verrebbe a coincidere con quello di folla, quale insieme di individui radunati occasionalmente che sviluppano pulsioni elementari ed emotive, o con quello di gente, un modo d’essere, un’attitudine conformista che forgia il cosiddetto uomo-m. in uno qualsiasi dei ruoli che si trova a occupare nella società. Dall’altra, la tendenza a considerare, in positivo, la m. come una formazione sociale di soggetti che mettono in comune le proprie esperienze di vita e agiscono solidalmente per un obiettivo condiviso o come una forma di sociabilità che si attua mediante la fusione parziale di un gruppo. Con l’intento di mediare fra queste posizioni e ottenere una definizione largamente denotativa del concetto di m., dopo averne passato in rassegna i possibili significati, W. Sombart (1924) escogita il concetto di m. statistica per dire di «una moltitudine di persone che agiscono in modo simile senza avere rapporti significativi fra loro».

È detta massificazione la tendenza, propria delle società industriali progredite, a portare a valori uniformi, standardizzati, il livello di vita, il comportamento e gli atteggiamenti spirituali dei singoli elementi di una comunità sociale, e il conseguente processo di annullamento dei caratteri e comportamenti individuali. Cultura di m. Tipo di cultura medio, diffuso dai moderni mezzi di comunicazione di m. (stampa, radio, televisione, cinema ecc.), prodotto con scopi prevalentemente commerciali e di intrattenimento, standardizzato, destinato al consumo nel tempo libero ma concepito anche come mezzo di innalzamento sociale di larghi strati popolari, tradizionalmente esclusi dalla fruizione dei beni culturali. Partito di m. Organizzazione politica sviluppatasi all’inizio del Novecento dopo l’introduzione del suffragio universale a opera, soprattutto, dei partiti socialisti, in grado di raccogliere consensi, rappresentare gli interessi e orientare le scelte politiche di vasti strati di popolazione. Scuola di m. Espressione usata, di solito in contrapposizione a scuola di élite, per indicare il fenomeno della generale estensione della scolarizzazione verificatasi nelle società contemporanee.

Teoria delle élite

La diffusione del termine m. nel linguaggio corrente delle scienze sociali deriva dagli sviluppi della teoria delle élite e dalle relative analisi sulla ineguale distribuzione del potere nella società. Il presupposto comune di queste analisi è che vi sia una dicotomia essenziale e irriducibile fra un ‘pubblico di élite’, composto dalla classe politica, dai gruppi dirigenti e dalle avanguardie intellettuali, e un ‘pubblico di m.’, contraddistinto come insieme di persone che posseggono un sistema di credenze cognitivamente povere ed emotivamente instabili, e che per questo si trovano in ogni caso esposte alla eterodirezione dei ‘pubblici’ di élite, sia nel caso si mobilitino per qualche progetto di mutamento sia nel caso si rivelino refrattarie a ogni ipotesi di coinvolgimento politico. Convergono verso queste conclusioni autori di formazione diversa ma in qualche modo legati alla teoria delle élite: da G. Mosca, capostipite di una letteratura ostile alla democrazia ‘di m.’, a C. Wright Mills, esponente di spicco della scuola americana, per il quale la m. (inerte e passiva) è l’esatto rovescio del concetto di opinione pubblica (critica e attiva), mentre altri autori come H. Arendt (1958) sottolineano l’opportunità di applicare il termine m. solo a quella maggioranza di persone politicamente neutrali o indifferenti che non possono essere integrate in nessuna organizzazione fondata su un interesse comune (e sarebbe questo, peraltro, il terreno sociale più favorevole allo sviluppo dei regimi autoritari o totalitari).

Le teorie sulla società di m. costituiscono dunque la naturale controparte della teoria delle élite, e mettono in luce come le conseguenze di taluni processi di modernizzazione – sviluppo economico, suffragio universale, urbanizzazione, consumismo, istruzione, tecnologia, mezzi di comunicazione – tendano a costruire una società di ‘uguali’ che, se da una parte poggia su una base assai estesa di democratizzazione, dall’altra tuttavia alimenta dinamiche di disgregazione e di isolamento individuale.

Tecnica

Il termine m. è usualmente sinonimo di terra: per es. collegamento a m., cioè con la terra. Alle volte, però, e più particolarmente in elettronica, collegamento a m. è il collegamento a una m. metallica (alla carcassa di una macchina elettrica, al telaio di un apparecchio radio ecc.), senza che ciò implichi necessariamente il collegamento della m. stessa alla terra; andare a m., si dice di un elemento di un apparecchio elettrico che accidentalmente vada a fare contatto con il telaio metallico dell’apparecchio stesso.