atomo

Secondo le teorie fisiche dell’antichità, particella di materia assolutamente semplice e non ulteriormente divisibile, dotata di qualità e quantità determinate. Nel linguaggio scientifico odierno, la più piccola particella di un elemento che rimane inalterata in ogni passaggio o reazione chimica. L’a. è cioè chimicamente inalterabile, indivisibile e indistruttibile, mentre può subire trasformazioni fisiche, come disintegrazione, trasformazione in altri atomi, eccitazione, fissione ecc.

L’a. nel 19° secolo

L’ipotesi della discontinuità della materia fatta propria da filosofi e scienziati moderni in formulazioni che riprendevano suggestioni dell’atomismo antico s’impose sul terreno della scienza sperimentale con la nascita della chimica, tra la fine del 18° e l’inizio del 19° sec. (J. Dalton, A. Avogadro ecc.). Restava tuttavia incerta e confusa la distinzione tra a. e molecole; fu soltanto nel 1858 che S. Cannizzaro poté dimostrare come le leggi di combinazione dei corpi e quelle della teoria cinetica dei gas trovino una giustificazione coerente solo se si ammette che a. e molecole siano cose diverse; che queste ultime siano formate dall’associazione di a. e a loro volta unendosi costituiscano i corpi. Nella seconda metà del 19° sec. la scoperta dei fenomeni inerenti al passaggio dell’elettricità nei gas, il simultaneo sviluppo della teoria elettromagnetica della luce e della spettroscopia, nonché una più approfondita indagine sui fenomeni elettrolitici, già da tempo noti, misero in luce come fosse infondata e insostenibile l’ipotesi dell’indivisibilità dell’a. e invece inevitabile quella dell’esistenza nel suo interno di particelle elettricamente cariche, alcune positive, altre negative (elettroni) in modo da compensarsi, poiché l’a. si presenta elettricamente neutro. Intanto, soprattutto a opera dei coniugi P. e M. Curie, si andavano sviluppando anche gli studi sulla radioattività, scoperta nel 1896 da H. Becquerel, dai quali veniva messo in luce che gli a. delle sostanze radioattive emettono sia radiazioni costituite da particelle elettriche positive e negative (raggi α e β), sia radiazioni di natura non più corpuscolare ma elettromagnetica (raggi γ).

Modelli atomici

All’inizio del 20° sec. per dar conto dell’intima struttura dell’a., vennero proposti diversi ‘modelli’.

L’a. di J.J. Thomson e di E. Rutherford. - Un primo modello atomico fu suggerito da J.J. Thomson, secondo il quale l’a. sarebbe stato costituito da una carica sferica positiva contenente al suo interno gli elettroni in numero tale da formare con l’elettricità positiva un insieme neutro; questo modello risultò però in netto contrasto con fatti sperimentali riguardanti sia la spettroscopia sia il passaggio delle particelle α attraverso la materia. Furono appunto questi ultimi fenomeni che suggerirono a E. Rutherford il suo modello (1911), secondo il quale l’a. è costituito da un certo numero Z ( numero atomico) di elettroni, più o meno grande a seconda dell’elemento chimico che si considera (idrogeno, elio ecc.), e da un’unica particella elettricamente positiva, detta nucleo. Dovendo l’a. essere elettricamente neutro, la carica del nucleo deve essere uguale, salvo il segno, a Z volte la carica e dell’elettrone. Le dimensioni degli elettroni e del nucleo sono trascurabili in confronto a quelle dell’a., in modo che si ritenne di potere, con approssimazione grandissima, considerare tali particelle come punti materiali. Il numero atomico Z coincide con il numero d’ordine del posto occupato dall’a. nel sistema periodico di Mendeleev (dall’idrogeno, che occupa il posto 1 della scala e il cui a. è costituito dal nucleo e da 1 elettrone, all’uranio che occupa il posto 92 e il cui a. è costituito dal nucleo e da 92 elettroni, agli elementi transuranici). La massa dell’a. è la somma delle masse degli elettroni e del nucleo; la massa totale degli elettroni è una frazione piccolissima della massa atomica (la massa di quiete, m₀, di un elettrone, 9,10710·10⁻³¹ kg, è circa 1/1840 volte la massa dell’a. d’idrogeno, che è l’a. più leggero). La massa dell’a. si può quindi praticamente considerare concentrata tutta nel nucleo, le cui dimensioni sono però estremamente piccole rispetto a quelle dell’intero a.: il diametro dell’a. è infatti dell’ordine di grandezza di 10⁻¹⁰ m, quello del nucleo di 10⁻¹⁵ m. Ciascun elettrone si muove intorno al nucleo sotto l’azione dell’attrazione elettrica. Secondo il modello di Rutherford, ci si può dunque figurare l’a. come una specie di microscopico sistema planetario, in cui il nucleo fa da Sole e gli elettroni da pianeti. Il modello di Rutherford dà conto della struttura dell’a. almeno nelle sue linee essenziali, ma contrasta con le leggi dell’elettrodinamica classica. Secondo questa, infatti, ogni carica elettrica animata di moto con velocità vettoriale non costante irradia nello spazio energia elettromagnetica: l’elettrone, essendo dotato di carica, dovrebbe, nel suo moto intorno al nucleo, irradiare continuamente energia elettromagnetica, ma in conseguenza di questa perdita di energia la sua orbita dovrebbe andare continuamente restringendosi e l’elettrone stesso finirebbe col cadere sul nucleo. Poiché ciò non si verifica, se ne deve concludere che le leggi dell’elettrodinamica classica non sono adatte alla descrizione dei fenomeni atomici. È questo il punto di partenza della teoria di N. Bohr (1913).

L’a. di N. Bohr. - L’ipotesi fondamentale della teoria di N. Bohr può enunciarsi nel modo seguente: i movimenti degli elettroni nell’a. sono determinati dalle leggi della meccanica classica, ma fra tutti i moti meccanicamente possibili possono realizzarsene solo alcuni (orbite permesse). Gli stati dell’a. che consentono il verificarsi dell’uno o dell’altro dei moti effettivamente possibili si dicono stati quantici o stati stazionari. Ammessa l’esistenza degli stati quantici, segue che anche l’energia dell’a. può assumere soltanto valori discreti: a ogni stato quantico corrisponde un diverso livello energetico e anche un’orbita diversa; le orbite più lontane dal nucleo hanno un livello energetico maggiore, cioè corrispondono a uno stato quantico più elevato. L’irraggiamento dell’energia elettromagnetica avviene soltanto quando un elettrone salta da un’orbita a un’altra che corrisponde a uno stato quantico minore. Precisamente se E_i e E_k sono le energie dell’a. nei due stati i e k, nel salto quantico i-k l’energia viene a variare di E_i−E_k e, se E_i>E_k la differenza di energia viene emessa sotto forma di radiazione elettromagnetica monocromatica di frequenza

[1]

dove h=6,6∙10⁻³⁴ J∙s è la costante di Planck. Il processo inverso avviene quando l’a. passa da uno stato quantico più basso a uno più elevato: l’a. allora assorbe energia in misura corrispondente alla differenza tra le energie dell’a. nei due stati quantici. La [1] non è che un’estensione al processo del salto quantico della relazione di Einstein W=hν tra l’energia W di un fotone e la frequenza ν della radiazione, ricavata nello studio della radiazione nera. Le ipotesi di Bohr, seppure semiempiriche, diedero impulso per una dozzina d’anni a uno sviluppo senza precedenti della fisica atomica. Esse sono state feconde di risultati specialmente nel campo della spettroscopia, consentendo il sistematico coordinamento di dati sino allora incoerenti. Secondo Bohr le orbite elettroniche corrispondenti agli stati stazionari sono circolari e sono, tra tutte le possibili orbite circolari, quelle il cui momento della quantità di moto è un multiplo intero di h/(2π). Tale ipotesi permette di arrivare a calcolare senza difficoltà il raggio r_n dell’orbita corrispondente allo stato quantico di indice n e l’energia E_n dell’elettrone nell’a. di idrogeno. Precisamente, indicando con ε₀ la costante dielettrica del vuoto, si trova

[2]

[3]

Per es., dalla [2], ponendo n=1, si ricava che il raggio della prima orbita stazionaria dell’idrogeno è 0,53∙10^–10 m, cioè 0,53 Å, valore che coincide, come ordine di grandezza, coi valori delle dimensioni atomiche già noti dalla teoria cinetica dei gas. Dalla [3], che si usa anche scrivere E_n=−Rh/n², dove R=m₀ e⁴/(8 ε₀² h³) è una costante detta di Rydberg, si può ricavare mediante la [1] la frequenza della riga spettrale emessa dall’a. nel salto quantico tra gli stati n′-mo e n-mo e si ottiene

[4]

fig. 1

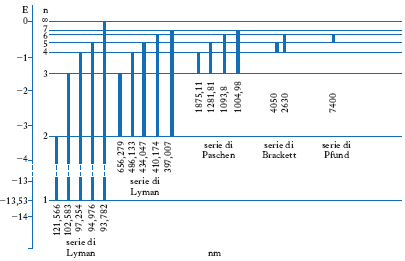
formula che dà risultati in perfetto accordo con l’esperienza (per n=1 e n′=2, 3, 4 ... si ritrova la serie spettroscopica di Lyman; per n=2 e n′=3, 4, 5 ... quella di Balmer; per n=3 e n′=4, 5, 6 ... la serie delle righe infrarosse di Paschen ecc.; fig. 1 ).

La teoria di A. Sommerfeld. - La regola data da Bohr per la scelta delle orbite stazionarie nel caso dei moti circolari venne generalizzata da A. Sommerfeld (1915-16) in modo da poterla applicare a una classe di movimenti molto più generali, e precisamente ai sistemi il cui moto è multiplamente periodico. Le condizioni di quantizzazione di Sommerfeld applicate all’a. d’idrogeno dettero ancora per l’energia degli elettroni dei diversi stati quantici l’espressione E_n=−Rh/n², ma misero in luce che, per un dato valore di n, quindi dell’energia, vi sono, non una sola, ma diverse orbite distinte per forma e per posizione. Precisamente per ogni valore di n esistono n possibili ellissi di differente eccentricità, contraddistinte con un numero d’ordine l che va da zero a (n−1), delle quali quella corrispondente a l=n−1 non è altro che la circonferenza considerata nella teoria di Bohr. Al numero l, il quale in definitiva fissa la forma dell’orbita, si dà il nome di numero quantico orbitale, o azimutale; a n, che determina l’energia di legame dell’elettrone, si dà invece il nome di numero quantico totale, o principale. Come abbiamo detto ora, l può valere 0, 1, 2, ..., (n−1) e n è un intero sempre maggiore di l, che quindi può valere (l+1), (l+2), ... Per n=∞ dalle [2], [3] si ricava r_∞=∞, E_∞=0; in tale caso l’elettrone sarebbe infinitamente lontano dal nucleo: l’a. è ionizzato. In relazione ai possibili valori di questi due numeri quantici, si hanno vari stati quantici, o livelli energetici, o, in concreto, si hanno varie orbite permesse. Seguendo un uso e una terminologia propria della spettroscopia, si conviene di raggruppare tali livelli in serie, indicate con una lettera a seconda del valore di l: per l=0 (n≥1), serie s; per l=1 (n≥2), serie p; l=2 (n≥3), serie d; l=3 (n≥4), serie f; l=4 (n≥5), serie g; l=5 (n≥6), serie h. Un livello energetico corrispondente a una certa coppia di valori possibili di n e di l viene indicato dando il valore di n e la sigla della serie corrispondente al valore di l: per es., livello 3 p, corrispondente a n=3, l=1. Si trova poi che si ha anche una quantizzazione spaziale, nel senso che l’orientamento delle orbite non può essere qualunque: la componente del momento della quantità di moto orbitale secondo una direzione assegnata deve valere m(h/2π), essendo m un intero, variabile tra −l e +l, che prende il nome di numero quantico magnetico. In definitiva, la teoria di Sommerfeld conferma i risultati di Bohr per quanto concerne l’energia di uno stato di dato numero quantico principale n, ma mostra in più che ciascun livello energetico E_n è degenere, nel senso che a esso corrispondono non uno ma diversi stati quantici aventi la stessa energia, corrispondenti a orbite differenti per eccentricità (differenti numeri quantici l) e orientamento (differenti numeri quantici m). Nel caso, che è poi quello generale, in cui gli elettroni dell’a. siano più di uno, per poter applicare le condizioni di Sommerfeld e ricavare i livelli energetici, sarebbe necessario risolvere il problema del moto di Z elettroni interagenti con il campo centrale del nucleo e tra loro: il problema presenta difficoltà matematiche tali da rendere praticamente impossibile una soluzione esatta.

Si usa chiamare anello elettronico l’insieme dei livelli, o, se si vuole, delle orbite elettroniche, corrispondenti a un medesimo valore di n; precisamente, per n=1 si ha l’anello K, per n=2 l’anello L, e così via (anello M, N, O, P per n=3, 4, 5, 6, rispettivamente). Il numero massimo di elettroni che possono costituire un anello si ottiene facilmente quando accanto ai tre numeri quantici prima definiti si aggiunga il numero quantico di spin, che dà conto della quantizzazione del momento della quantità di moto (o angolare) intrinseco (o di spin) dell’elettrone; la proiezione del momento della quantità di moto di spin secondo una direzione assegnata può assumere solo i valori ±(h/2π)/2, ai quali sono associati i valori 1/2 del numero quantico di spin. A norma del principio di esclusione di Pauli (1925), due elettroni non possono essere caratterizzati dalla stessa quaterna di numeri quantici; in uno stato corrispondente a un’assegnata terna di valori possibili per n, l, m possono quindi trovarsi al più due elettroni, dotati però di numeri quantici di spin di segno opposto: il numero di elettroni che possono trovarsi in un dato anello è quindi il doppio di quello che si ottiene considerando le possibilità offerte dai primi tre numeri quantici, cioè 2n². Si possono avere quindi al più 2 elettroni nell’anello K, 8 nell’anello L, 18 in M, 32 in N ecc.; un anello, e anche un livello, si dicono completi, o pieni, se contengono il numero massimo consentito di elettroni. Va ricordato, poi, che per spiegare alcuni fenomeni relativi all’emissione e all’assorbimento della radiazione elettromagnetica viene introdotto un altro numero quantico elettronico, e precisamente il numero quantico interno, j, pari alla somma del numero quantico orbitale l e del numero quantico di spin s (e quindi è j=1/2, 3/2, 5/2, ...). In conseguenza di ciò, è usuale suddividere gli anelli elettronici in vari sottoanelli in relazione ai possibili valori degli anzidetti numeri quantici.

Per rappresentare lo stato dell’intero a. si ricorre al modello vettoriale dell’atomo. Precisamente, si indica con L il risultante dei momenti delle quantità di moto orbitali dei singoli elettroni, con S il risultante dei momenti di spin dei singoli elettroni, con j il risultante di L e di S. Le condizioni di quantizzazione portano che il modulo di L sia nullo o multiplo intero di (h/2π), il modulo di S sia un multiplo intero o semiintero di (h/2π). Il modulo del vettore J può assumere uno dei valori ∣L−S∣, ∣L−S+1∣ ..., ∣L+S−1∣, ∣L+S∣. Tale simbolismo vettoriale si rivela particolarmente utile nella trattazione delle proprietà magnetiche della materia.

Configurazione elettronica dell’atomo. - La teoria di Bohr-Sommerfeld ebbe un brillante successo nell’interpretazione teorica delle ricerche sugli spettri degli a. complessi e delle molecole. L’ipotesi fondamentale della teoria di Bohr, cioè la possibilità dell’esistenza di diversi livelli energetici per l’a., poneva, tra gli altri, il problema del modo come si distribuiscono, a una data temperatura, fra i vari stati quantici gli a. di un determinato corpo. Con i metodi della meccanica statistica si dimostra che in generale i livelli più probabili sono quelli di energia più bassa; generalmente anzi i valori delle energie sono tali che, per temperature non elevatissime, la grande maggioranza degli a. si trova nello stato di minima energia, che viene perciò detto stato fondamentale. In tale stato fondamentale, dunque, gli elettroni si dispongono in modo da occupare ordinatamente i livelli di energia minima, e cioè, se si vuol parlare in termini di orbite, in modo da occupare quella tra le orbite permesse che sia più vicina al nucleo. In base a questo principio e a quanto detto precedentemente, è quindi possibile, assegnato che sia il numero atomico Z, ‘costruire’ la configurazione elettronica dell’a., cioè determinare i livelli che verranno successivamente occupati dagli elettroni disponibili.

fig. 2

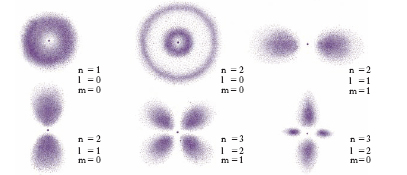
La ‘nuova meccanica’. - Anche nel periodo di maggior successo, gli anni dal 1913 al 1925, la teoria di Bohr-Sommerfeld appariva ben lontana dal dare una risposta definitiva ai problemi della fisica atomica. Oltre alla già accennata difficoltà matematica praticamente insuperabile di applicazione del metodo nel caso di a. con più elettroni, era dubbia la legittimità di una teoria alla cui base stava una specie di compromesso tra i principi della fisica classica, peraltro accolti, in modo arbitrario, solo in parte, e i principi quantistici. Queste e altre circostanze facevano sentire ormai viva la necessità di una profonda revisione delle stesse basi logiche della fisica atomica, revisione che doveva portare alla nuova meccanica o meccanica quantistica nelle due forme – dimostratesi poi sostanzialmente equivalenti – di meccanica delle matrici e di meccanica ondulatoria. Questa è sorta fondamentalmente a opera di W. Heisenberg e di E. Schrödinger, rispettivamente, tra il 1925 e il 1926. La nuova meccanica, alla quale contributi di essenziale importanza sono stati portati anche da P.A.M. Dirac, si è rivelata molto feconda d’idee nuove nel campo della teoria delle righe spettrali, finalmente costituita su basi razionali, nel campo della chimica, ove trovano la loro spiegazione i fenomeni della valenza, nella teoria della conduzione elettrica, della radioattività ecc. L’idea intuitiva dell’elettrone simile a un punto materiale che percorra nell’a. una delle orbite permesse secondo la teoria di Bohr-Sommerfeld è distrutta dalla nuova teoria: il principio di indeterminazione di Heisenberg stabilisce che non ha più un senso preciso parlare di posizione e di velocità simultaneamente e perfettamente determinate, e quindi viene meno il concetto classico di traiettoria. Se non si vuole abbandonare il linguaggio prima usato per descrivere la struttura atomica, occorrerà tenere ben presente ciò che va inteso per orbita elettronica. Dovendo rinunciare alla possibilità di determinare la posizione di un elettrone di data energia in un istante t, ci si dovrà riferire alla probabilità P che l’elettrone considerato si trovi, all’istante t, in un certo volumetto dv: potremo allora intendere, in via approssimata, come orbita elettronica il luogo dei punti dello spazio in cui P è massima. Nella fig. 2 è rappresentato schematicamente l’andamento della parte radiale di P intorno al nucleo per elettroni in vari livelli, la probabilità risultando tanto maggiore quanto maggiore è l’addensamento dei punti: sostituire rappresentazioni del genere con linee (orbite) circolari appare in effetti cosa largamente approssimata, se pure comoda ed espressiva.

Qualificazioni dell’atomo

A. eccitato A. nel quale elettroni si muovono su orbite corrispondenti a livelli energetici più alti di quelli che si hanno nell’a. non eccitato, cioè nel cosiddetto stato fondamentale A. esotico A. instabile nel quale una particella pesante carica negativamente si sostituisce a uno degli elettroni atomici.

A. ionizzato A. che ha un numero di elettroni minore (a. elettropositivo, ione monoatomico positivo) oppure maggiore (a. elettronegativo, ione monoatomico negativo) del numero atomico.

A. marcato A. radioattivo usato come indicatore radioattivo.

A. mesonico (o mesico) A. instabile nel quale un elettrone è rimpiazzato da un mesone negativo.

A. neutro A. non ionizzato, in cui cioè il numero degli elettroni è pari al numero atomico.

A. normale A. che non è ionizzato né eccitato.

A. nudo A. in condizioni normali, non vestito, cioè non circondato da alcun campo elettromagnetico né da particelle virtuali. A. padre A. radioattivo dal decadimento del quale si originano a. di specie diversa.

A. unito Insieme di due a. i cui nuclei siano talmente vicini da poterli considerare come se fossero uno solo, di carica pari alla somma delle cariche dei due nuclei.

A. vestito A. circondato da un campo elettromagnetico non risonante con alcuna delle sue transizioni: in tali condizioni le proprietà dell’a. sono connesse alle interazioni virtuali con il campo e risultano molto diverse da quelle di un a. nudo, cioè di un a. che non sia circondato da alcun campo.

A. gigante o di Rydberg A. il cui elettrone più esterno si trova in uno stato eccitato con un grande numero quantico principale (n≫1); ha dimensioni di alcuni μm con una forma che dipende dal valore del numero quantico azimutale (dalla forma sferica per l=0 alla forma di un disco circolare per l=n−1); le sue proprietà sono molto vicine a quelle previste dalla teoria semiclassica di Bohr. La presenza di a. giganti è stata riconosciuta nello spazio interstellare, dove sono generati dalla ricombinazione radiativa di elettroni e ioni e permangono indisturbati, a causa della bassa densità di materia presente, per tempi abbastanza lunghi, decadendo lentamente allo stato fondamentale.

Filosofia

L’atomismo è la concezione secondo la quale l’intera realtà è composta di a., cioè di particelle indivisibili. Nelle teorie fisiche dell’antichità, il ricorso a una concezione corpuscolare della materia, con cui si può far cominciare la storia dell’atomismo, rispose all’esigenza di spiegare alcuni fenomeni, come quello della condensazione e rarefazione e quello della combinazione e risoluzione di elementi diversi nei misti. L’a. veniva concepito come una quantità minima, di fatto non ulteriormente divisibile (gli a. tutti diversi per forma e grandezza si differenziano anche fra di loro per ordine e posizione): così nella più antica dottrina atomistica, quella di Leucippo e Democrito. Più tardi l’atomismo fu ripreso da Epicuro, il quale dotò gli a. di un intrinseco impulso al moto e concepì il loro aggrupparsi come provocato da una casuale ‘deviazione’ rispetto al moto di caduta verticale. Attraverso Lucrezio, l’atomismo di Epicuro passò nell’ambiente romano. Nel Medioevo restano scarse tracce dell’atomismo antico, dato soprattutto il prevalere di una fisica essenzialmente qualitativa: poi il trionfo della fisica aristotelica e la facile associazione polemica dell’atomismo con l’epicureismo (inteso come materialismo e immoralismo) fecero perdere ogni traccia di atomismo. Nel Rinascimento, la riscoperta di Lucrezio e di Epicuro (tramite Diogene Laerzio, che faceva anche conoscere l’atomismo democriteo) riporta l’a. in voga negli ambienti della nuova filosofia (G. Bruno) e della nuova scienza. La concezione atomistica si fece più precisa per merito in particolare di G. Galilei, di R. Descartes e di P. Gassendi, che si può considerare, nel 17° sec., il suo più coerente difensore (ancorché con una costante preoccupazione di conciliare l’epicureismo con le fondamentali verità della teologia naturale). Sull’atomismo si basò una generale concezione del mondo capace di eliminare la fisica aristotelica e di offrire un’ipotesi valida alla spiegazione ultima dei fenomeni naturali nella forma democritoepicurea. In seguito, il problema atomistico si spostò sempre più sul terreno della scienza sperimentale.