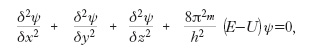meccànica quantìstica
meccànica quantìstica Teoria fisica che descrive in termini di probabilità statistica il comportamento dei sistemi di dimensioni atomiche o subatomiche (elettroni, nuclei, atomi, molecole ecc.) per i quali non sono verificate le leggi della meccanica classica e dell'elettromagnetismo. Un collegamento tra descrizione classica e quantistica è offerto dal principio di corrispondenza (→ corrispondenza, principio di) introdotto da N.H.D. Bohr.
Aspetti fondamentali
Elementi distintivi della teoria sono la discontinuità nella variazione delle grandezze fisiche (→ quantizzazione), la capacità di interpretare fenomeni che abbiano sia carattere ondulatorio sia carattere corpuscolare (→ complementarità, principio di), l'influenza dei procedimenti di misura sui valori delle misurazioni effettuate e l'impossibilità di determinare con precisione arbitraria grandezze tra loro coniugate come posizione e velocità (→ indeterminazione, principio di). La m.q. ha consentito una soddisfacente interpretazione di vari dati sperimentali, quali la diffrazione degli elettroni, gli spettri atomici, l'effetto fotoelettrico, l'effetto Compton ecc., e ha permesso di spiegare fenomeni macroscopici come la condensazione di Bose-Einstein, la superconduttività, la superfluidità.
Meccanica ondulatoria e meccanica delle matrici
La m.q. è sorta quasi contemporaneamente sotto due forme in apparenza molto diverse poi rivelatesi equivalenti: la meccanica ondulatoria di E. Schrödinger (1926) e la meccanica delle matrici di W.K. Heisenberg (1925). La meccanica ondulatoria si basa sull'intuizione di L.-V. de Broglie (1924) di associare a ogni particella un'onda ed è stata sviluppata in maniera sistematica da Schrödinger. La teoria si propone di determinare la probabilità che una particella si trovi in un dato istante in un elemento di volume, e per il calcolo di questa probabilità introduce una funzione, in genere complessa, ψ (x, y, z, t ), detta funzione d'onda. Il modulo quadro della funzione d'onda ∣ψ (x, y, z, t )∣2 moltiplicato per l'elemento di volume dà la probabilità (secondo l'interpretazione di M. Born) che la particella si trovi all'istante t in un intorno del punto di coordinate x, y, z. Se E è l'energia totale della particella, ψ può essere posta nella forma
ψ =u (x, y, z )−2πiνt
con ν =E/h; ψ deve soddisfare l'equazione di Schrödinger,
dove U è l'energia potenziale del campo di forza che agisce sulla particella. Nella formulazione della m.q., dovuta principalmente a Heisenberg (1925) e nota come meccanica delle matrici, a ogni grandezza fisica corrisponde una matrice i cui elementi sono numeri collegati a quantità direttamente osservabili e le ordinarie relazioni algebriche fra grandezze fisiche si traducono in relazioni tra le matrici corrispondenti.
Sviluppi successivi
A P.A.M. Dirac (1928) si devono i primi sviluppi di un formalismo in grado di coniugare m.q. e teoria della relatività ristretta (m.q. relativistica). In questo approccio, possono essere ricavate proprietà quali il momento angolare intrinseco (spin) dell'elettrone, il suo momento magnetico e l'esistenza dell'antimateria (→ positrone). Nella formulazione attuale della m.q. ogni stato del sistema viene rappresentato mediante un vettore appartenente a un opportuno spazio vettoriale astratto e ogni variabile dinamica è descritta come un operatore di stato definito sullo spazio. L'evoluzione temporale del sistema è affrontata considerando fissati i vettori e variabili gli operatori o viceversa, a seconda dell'approccio (rispettiv. di Heisenberg o Schrödinger) scelto.
La misura in meccanica quantistica
Uno degli aspetti più delicati della m.q. è rappresentato dall'operazione di misura. Assegnata una variabile dinamica A si otterrà un ben determinato risultato a dalla sua misura solo se il vettore di stato che descrive il sistema verifica la condizione Aψ =aψ. In tal caso ψ è un autostato di A e a è il corrispondente autovalore. Se il vettore di stato non soddisfa la precedente equazione per la variabile dinamica si può solo assegnare la probabilità di ottenere il risultato a effettuando la misura. Il carattere intrinsecamente probabilistico della m.q. ha trovato in A. Einstein un tenace avversario e ancor oggi i problemi sollevati dalla misura in m.q. rappresentano uno degli aspetti più controversi della teoria.