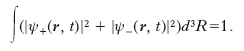spin

spin Termine («rotazione») introdotto inizialmente per indicare il momento della quantità di moto intrinseco dell’elettrone, ipotizzato (1925) da S.A. Goudsmit e G.E. Uhlenbeck allo scopo di dar conto di alcuni fatti sperimentali. La considerazione di questa grandezza è stata poi estesa alle particelle elementari in genere.

S. dell’elettrone

Lo studio teorico del comportamento di un atomo in un campo magnetico porta alla separazione di ogni livello d’energia imperturbato in (2l+1) livelli, dove l è il numero quantico azimutale. Tale risultato è in disaccordo con i risultati sperimentali offerti dall’analisi delle righe spettrali emesse in presenza di un campo magnetico omogeneo (effetto Zeeman), dove ogni livello si scinde in 2(2l+1) livelli, e dai risultati dell’esperienza di O. Stern e W. Gerlach, dove un fascio di atomi per effetto di un forte campo magnetico disomogeneo si scinde in più fasci anche nel caso che l’elettrone atomico sia in uno stato con l=0. Tali risultati sperimentali trovano una spiegazione soddisfacente se si assume che l’elettrone possieda un momento angolare intrinseco (momento di s. o semplicemente s.). Questo momento ha grandezza costante ed è tale che la sua componente in una direzione qualsiasi vale sℏ, essendo ℏ la costante di Planck ridotta, s il numero quantico di s., pari a ±1/2; talora anche questo numero quantico è chiamato s. per semplicità. A tale momento angolare è associato un momento magnetico intrinseco pari a un magnetone di Bohr. In rapporto a tale momento magnetico si parla a volte anche di s. magnetico, dando il nome di s. meccanico allo s. vero e proprio. In un atomo, gli s. dei vari elettroni si compongono con i momenti delle quantità di moto orbitali (accoppiamento s.-orbita), dando luogo al momento angolare totale: un tale tipo di accoppiamento spiega la struttura fine degli spettri atomici.

Analogamente a quanto si è constatato per l’elettrone, anche per i nuclei, partendo da osservazioni spettroscopiche, si è verificata l’ipotesi di W. Pauli secondo cui essi possiedono un momento angolare (s. nucleare o dei nuclei); quest’ultimo, accoppiandosi al momento angolare totale degli elettroni, dà luogo al momento angolare totale dell’atomo; in tal modo è possibile dar conto della struttura iperfine degli spettri atomici.

S. e meccanica quantistica

L’introduzione dello s. richiede una modifica nel formalismo della meccanica quantistica. Nel caso non relativistico, per una particella di s. 1/2, la funzione d’onda ψ(r, t) viene sostituita da una funzione, ψ(r, s, t), dipendente anche dalla variabile di s. s; poiché questa può assumere due soli valori, s=±1/2, la funzione d’onda di una particella di s. 1/2 equivale a una coppia di funzioni, ψ+(r, t), ψ−(r, t) il cui modulo quadro rappresenta la densità di probabilità di trovare, a un certo istante t, la particella nella posizione r, e con lo s. parallelo o antiparallelo a una direzione assegnata; la normalizzazione è

Le funzioni ψ+(r, t), ψ−(r, t) costituiscono le due componenti di un ente matematico, detto spinore o, anche, spinore di Pauli, caratterizzato da specifiche proprietà di trasformazione sotto le rotazioni spaziali. Gli operatori che agiscono sullo spazio di Hilbert degli stati della particella diventano matrici 2×2, i cui elementi sono, in generale, operatori che agiscono sulle coordinate spaziali e sul tempo. Ogni matrice 2×2 può essere espressa con una combinazione lineare della matrice unità e delle 3 matrici di Pauli σi, i=1, 2, 3; in particolare, si possono definire gli operatori Si=(ℏ/2)σi, che rappresentano il momento di s. e quindi generano le rotazioni intorno agli assi xi, per gli spinori di Pauli. Contrariamente a quanto accade per le funzioni ordinarie, che dopo una rotazione di 2π riacquistano il valore iniziale, gli spinori cambiano segno dopo un giro, ed è solo dopo una rotazione di 4π che riassumono, anche nel segno, il valore iniziale.

Se, per una particella con massa diversa da zero, si indica con μ il massimo valore che può assumere la proiezione, lungo una direzione arbitraria, del momento angolare della particella in un riferimento in cui essa sia in quiete, la particella è detta possedere s. μ ed è descritta, anche in una trattazione relativisticamente invariante, da una funzione d’onda con (almeno) 2μ+1 componenti; quando si considerano anche le simmetrie per inversione spaziale o temporale e per coniugazione di carica, il numero di tali componenti raddoppia. Gli stati di una particella di massa nulla sono caratterizzati da un parametro λ=0, ±1/2, ±1, ..., il cui modulo definisce lo s. di tale particella e il cui valore è interpretabile come la proiezione dello s. lungo la direzione del moto (➔ elicità); per es., si ha λ=±1 per il fotone, al quale si attribuisce s. 1, λ=−1/2 per i neutrini, il cui s. vale 1/2.

Un teorema generale collega lo s. delle particelle con le loro proprietà di simmetria rispetto allo scambio di tutti i gradi di libertà: le particelle di s. semintero si comportano in modo antisimmetrico rispetto allo scambio e seguono perciò la statistica di Fermi-Dirac, mentre quelle di s. intero si comportano in modo simmetrico e seguono la statistica di Bose-Einstein. La dimostrazione del teorema spin-statistica può essere fatta nell’ambito della teoria relativistica dei campi quantizzati, in cui si può vedere che l’attribuzione della statistica sbagliata comporta o la violazione del principio di causalità, oppure dà luogo a classi di soluzioni per cui l’energia non è limitata inferiormente e, quindi, impedisce l’esistenza di uno stato fondamentale stabile.

Locuzioni particolari

Con s. flip («rovesciamento dello s.») si indica un’inversione dello s., cioè il cambiamento di segno della sua componente lungo un determinato asse.

Lo s. isotopico è una grandezza, chiamata anche isospin, introdotta in fisica delle particelle elementari (➔) per contraddistinguere i vari stati di carica di uno stesso adrone (➔ isotopi).

Le onde di s. sono eccitazioni elementari di un sistema ferromagnetico, costituite da variazioni periodiche dell’orientamento dei momenti magnetici atomici; in una trattazione quantistica tali eccitazioni sono dette magnoni.

Con risonanza di s. si indica genericamente la risonanza paramagnetica e ferromagnetica.

In meccanica statistica, si dicono sistemi di s. quei sistemi costituiti da particelle la cui energia riceve contributo solo dall’accoppiamento magnetico tra le particelle ed eventualmente tra esse e un campo esterno. La descrizione di tali sistemi fa uso di variabili di s. che, in genere, possono assumere solo valori discreti. Al variare del range e del segno dell’interazione tra le particelle si passa da sistemi ordinati, per es., il modello di Ising (➔ Ising, Ernest), a sistemi disordinati, quali i vetri di s. (➔ vetro). I sistemi di s. sono molto studiati nella meccanica statistica perché per essi possono essere dimostrate molte proprietà con completo rigore matematico, evitando le complicazioni tecniche che sorgono nell’esame di sistemi di particelle le cui coordinate assumono valori in un insieme continuo; per es., è possibile mostrare rigorosamente che in alcuni sistemi ordinati si possono avere transizioni di fase. Lo studio di questi sistemi presenta ancora molti problemi: per es., i sistemi disordinati hanno una struttura di stati fondamentali che costituisce un campo di ricerca di grande attualità e in parte ancora non chiarito.