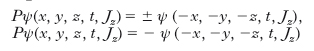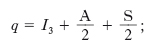particelle elementari
Denominazione generica dei costituenti ultimi della materia e della radiazione.
Definizione
Adottando l’atteggiamento pragmatico inaugurato da A.-L. Lavoisier nei confronti degli elementi chimici, si può riservare la denominazione di p. a quei costituenti della materia che non mostrano una struttura interna. In questa accezione sono da designare come elementari le particelle fondamentali (quark e leptoni), costituenti tutte le altre particelle note, e i bosoni di gauge, mediatori delle interazioni fra quark e leptoni. Peraltro, per ragioni storiche e pratiche, si qualificano comunemente come p. tutte le particelle (subnucleari) di dimensioni minori o uguali a ∼10−15 m (mentre quark e leptoni hanno dimensioni minori o uguali a ∼10−18 m). La definizione di p. richiede in effetti alcune considerazioni preliminari. La struttura interna della materia mostra vari livelli, ciascuno dei quali è pertinente a una ben determinata classe di fenomeni avente caratteristiche del tutto peculiari, in modo tale che ogni classe può sembrare una distinta branca della fisica. Ciascun livello è in particolare caratterizzato dall’ordine di grandezza delle dimensioni spaziali (R) dei sistemi in gioco e dei trasferimenti di energia (ΔE) che in essi hanno luogo. Allo stato attuale delle conoscenze sono noti quattro livelli: I) molecolare (R∼10−9 m, ΔE∼10−1 eV); II) atomico (R∼10−10 m, ΔE∼1 eV); III) nucleare (R∼10−14 m, ΔE∼106 eV); IV) subnucleare (R∼10−15-10−16 m, ΔE∼108-109 eV); la situazione è riassunta nella tab. 1.
In conformità alle leggi della meccanica quantistica i gradi di libertà interni di una struttura concernente un dato livello sono ‘congelati’ se non è messa in gioco un’energia sufficiente per eccitarli e la struttura stessa, confinata nello stato fondamentale, non si manifesta: per es., l’atomo si comporta come privo di struttura interna nella cinetica dei gas, il nucleo ha tale comportamento in fisica atomica ecc. Le p. in senso proprio sono quindi quelle fondamentali del IV livello, mentre l’accezione più comune (cui ci si riferirà anche nel seguito) include anche quelle fondamentali del III livello.
Per il concetto di p. in teoria quantistica del campo ➔ campo.
Cenni storici
L’idea che la materia consista di poche specie di costituenti elementari semplici e immutabili affonda le sue radici nell’antichità classica, in particolare nell’atomismo greco, ma solo all’inizio del 19° sec., grazie allo studio dei rapporti ponderali nelle reazioni chimiche (J. Dalton, W. Prout), la teoria atomica della materia comincia a poggiare su solide evidenze sperimentali. Nel corso del secolo la teoria atomica si va precisando (A. Avogadro, S. Cannizzaro) e trova ampia conferma nell’interpretazione microscopica dei fenomeni termici (R. Clausius, J.C. Maxwell, L. Boltzmann). Misurazioni indirette forniscono le prime stime delle dimensioni atomiche (∼10−10 m). Sul finire del 19° sec. le scoperte dell’elettrone (J.J. Thomson) e della radioattività (H. Becquerel) indicano chiaramente che gli atomi sono strutture complesse, come già suggerito dagli spettri di emissione e di assorbimento delle varie specie atomiche. Lo studio della distribuzione spettrale della radiazione elettromagnetica in equilibrio termico evidenzia (A. Einstein, 1905) il comportamento corpuscolare della radiazione (in termini di ‘quanti di luce’ o ‘fotoni’) che viene definitivamente confermato dalla scoperta dell’effetto Compton (1922). Ricerche condotte sulla diffusione a grande angolo delle particelle α emesse da sostanze radioattive nell’attraversamento della materia indicano (E. Rutherford, 1911) che gli atomi sono costituiti da un nucleo massivo molto piccolo rispetto alle dimensioni atomiche, intorno al quale sono distribuiti gli elettroni. Le dimensioni del nucleo risultano essere dell’ordine di 10−14 m.
Negli anni tra il 1900 e il 1927, nello studio dei fenomeni atomici e subatomici emerge l’inadeguatezza della fisica classica a trattare il comportamento dei costituenti dell’atomo e prende corpo (N. Bohr, W. Heisenberg, E. Schrödinger, P.A.M. Dirac) il nuovo approccio ai problemi microscopici costituito dalla meccanica quantistica. Ben presto anche il nucleo, grazie allo studio delle reazioni nucleari (e come indicato dai processi radioattivi che proprio in esso hanno sede), mostra di essere un sistema complesso: poiché bombardando nuclei leggeri con particelle α vengono espulsi protoni (E. Rutherford, 1919) e neutroni (J. Chadwick, 1932), queste particelle sono identificate come i costituenti del nucleo (nucleoni). Le dimensioni di protone e neutrone risultano essere dell’ordine di 10−15 m. A questo punto sembra completo il quadro delle particelle fondamentali, comprendente elettrone, protone, neutrone, fotone e l’antiparticella dell’elettrone (prevista teoricamente da P. A.M. Dirac, e osservata da C.D. Anderson nella radiazione cosmica nel 1932).
Nel 1933 E. Fermi formula la teoria della radioattività β in termini di decadimento di un neutrone del nucleo in un protone, un elettrone e un neutrino, quest’ultimo ipotizzato da W. Pauli per assicurare la conservazione dell’energia. Nel 1936 viene osservata da C.D. Anderson e S.H. Neddermeyer nella radiazione cosmica una particella instabile con massa intermedia tra quelle dell’elettrone e dei nucleoni, che viene allora denominata mesotrone (o mesone, oggi nota come muone) e identificata con il mediatore delle forze nucleari, previsto teoricamente nel 1935 da H. Yukawa. Nel 1946 M. Conversi, E. Pancini e O. Piccioni dimostrano sperimentalmente che il mesotrone interagisce debolmente con la materia nucleare e quindi non può essere la particella di Yukawa; questa (oggi nota come mesone π o pione) viene scoperta subito dopo, sempre nella radiazione cosmica, da C.M. Lattes, H. Muirhead, G. Occhialini e C.F. Powell. Poco dopo vengono scoperti nella radiazione cosmica in alta quota le prime particelle ‘strane’, i mesoni o kaoni, la Λ ecc. Nel 1956 C. Cowan e F. Reines rivelano per la prima volta un neutrino osservando la reazione νe+p→n+e+.
Negli anni 1950, con l’avvento delle grandi macchine acceleratrici, inizia lo studio sistematico delle particelle note e viene scoperto un gran numero di nuove particelle: gli stati eccitati dei nucleoni (a partire dal 1951 con E. Fermi) e degli iperoni, nuovi mesoni, l’Ω− (nel 1964), la particella J/ψ (nel 1974) e i suoi stati eccitati, i mesoni con charm D, il leptone τ o tauone (nel 1975), la particella Y (nel 1977) e i suoi stati eccitati, i mesoni B con beauty, i bosoni Z e W± (nel 1983).
Sono oggi note oltre 500 particelle subnucleari. È da sottolineare però che nonostante l’elevatissimo numero di tali particelle, la materia di cui è costituito l’Universo è composta quasi esclusivamente di elettroni, protoni e neutroni, di fotoni e di neutrini, cioè di particelle stabili che non decadono in altre particelle (si ricorda che il neutrone, instabile se libero, non può decadere quando compone un nucleo stabile). Tutte le altre particelle sono instabili e sono prodotte, direttamente o indirettamente, nell’urto di particelle stabili dotate di energia sufficientemente elevata, come quelle che costituiscono la radiazione cosmica o quelle che vengono ottenute in laboratorio con le macchine acceleratrici.
Inoltre, già a partire dall’inizio degli anni 1960 è emerso che i cosiddetti adroni, che costituiscono la quasi totalità delle particelle oggi note, sono combinazioni di sole 6 particelle, i quark, e questa ipotesi ha ricevuto numerose, significative conferme sperimentali.
Le particelle fondamentali
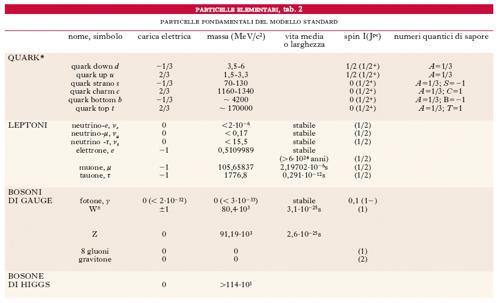
Allo stato attuale delle conoscenze il cosiddetto Modello Standard delle p. considera come particelle fondamentali i quark (di 6 tipi o sapori, ciascuno in 3 repliche di colore), 6 leptoni, 12 bosoni di gauge (fotoni) e uno o più bosoni scalari (bosoni di Higgs). A essi va aggiunto il gravitone, quanto del campo gravitazionale. La tab. 2 elenca queste p. fondamentali e alcune delle loro proprietà, che verranno discusse nel seguito.
Il primo gruppo di particelle che figura nella tab. è costituito dai bosoni di gauge, le particelle con spin 1 (in unità di ℏ) che mediano le interazioni fondamentali (➔ interazione): il fotone è il mediatore delle interazioni elettromagnetiche, i bosoni W± e Z delle interazioni deboli; si hanno solo evidenze indirette sugli 8 gluoni, di carica elettrica e massa zero, che mediano le interazioni forti. Il gravitone, mediatore delle interazioni gravitazionali, non è stato sinora rivelato sperimentalmente; per la loro piccolissima intensità, alle energie accessibili, le interazioni gravitazionali non danno effetti osservabili in fisica delle particelle elementari.
Il secondo gruppo è costituito dai leptoni, le 6 particelle a spin 1/2 che non sono soggette a interazioni forti.
Il terzo gruppo è costituito dai quark, le particelle fondamentali soggette a interazioni forti.
La sperimentazione
Fino agli inizi degli anni 1950 la radiazione cosmica ha costituito l’unico campo di indagine per la ricerca di nuove particelle subnucleari; ma a partire da quegli anni, la realizzazione di acceleratori sempre più potenti ha consentito lo studio sistematico delle proprietà delle particelle e la produzione di nuove particelle con massa sempre più elevata. Inizialmente la strategia impiegata nella sperimentazione con le macchine acceleratrici (sincrotroni e acceleratori lineari) era basata sullo studio delle collisioni di ‘particelle proiettile’ di alta energia (i protoni o gli elettroni accelerati, o particelle secondarie prodotte da questi) contro ‘particelle bersaglio’ ferme (i protoni, i neutroni, gli elettroni presenti in una qualunque porzione di materia). Questa strategia presenta però il grave inconveniente che al crescere dell’energia del proiettile una frazione sempre più piccola di questa energia è utile per produrre nuove particelle o per indagare la struttura del bersaglio. L’energia utile è infatti quella disponibile nel sistema di riferimento del centro di massa del sistema proiettile-bersaglio che, nel caso della collisione di due particelle di uguale massa M, una di elevata energia E≫Mc2 e l’altra ferma, vale circa (2Mc2E)1/2; la frazione utile di E, pari a circa (2Mc2/E)1/2, decresce quindi al crescere di E (per es., nella collisione contro un elettrone fermo di un elettrone con energia cinetica di 1 keV, l’energia utile è il 50%, mentre a un’energia cinetica di 1 GeV l’energia utile scende al 3% e si riduce al 3‰ a 100 GeV). Questo inconveniente non si manifesta se si realizza la collisione tra particelle animate da quantità di moto uguali e opposte, in quanto il sistema del centro di massa coincide in questo caso con quello del laboratorio e quindi tutta l’energia fornita dalle particelle è utile. Nel 1960 B. Touschek attuò questo tipo di collisione ideando e subito dopo realizzando presso i Laboratori nazionali di Frascati il primo anello di accumulazione a fasci collidenti per elettroni e positroni. Gradualmente gli anelli di collisione si sono imposti e oggi i più potenti acceleratori sono di questo tipo.
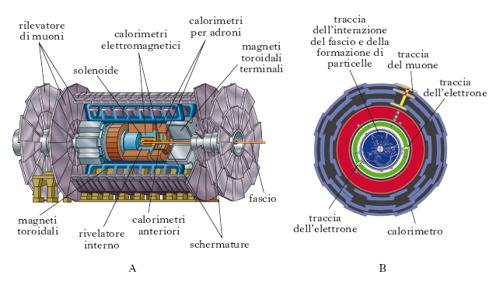
A partire dalla seconda metà degli anni 1970 ha ricevuto grandissimo impulso anche la ricerca sulle particelle condotta in laboratori sotterranei per lo studio di eventi rari (come l’eventuale decadimento del protone) in assenza quasi completa di fondo, dei neutrini solari (➔ neutrino) o di raggi cosmici di altissima energia. Per la rivelazione delle particelle subnucleari prodotte in una collisione ci si serve di complessi apparati sperimentali (che possono raggiungere dimensioni dell’ordine di 1000 m3; fig. 1) costituiti da un gran numero di rivelatori che permettono di misurare con notevole precisione l’istante e/o il punto in cui sono attraversati dalle particelle e quindi di ricostruire la traiettoria di queste. Data l’estrema complessità degli apparati, che possono comprendere svariate decine di migliaia di rivelatori, a ciascuno dei quali è connessa una catena di circuiti elettronici che ne elaborano i segnali, il loro controllo, la loro gestione, la memorizzazione dei dati forniti dai rivelatori, sotto forma di segnali elettrici, e la parziale ricostruzione geometrico-cinematica degli eventi prodotti nelle collisioni sono affidati a calcolatori elettronici on-line, che eseguono una prima selezione degli eventi, così come a potenti calcolatori off-line è affidata l’analisi completa degli eventi raccolti.
Gli apparati sperimentali generalmente forniscono la misura della quantità di moto delle particelle a partire dalla misura della curvatura delle traiettorie in un campo magnetico noto. In alcune circostanze è possibile misurare la velocità di una particella misurando il tempo che impiega a coprire una distanza nota o dalle caratteristiche della radiazione Čerenkov prodotta. L’energia delle particelle si determina facendole fermare in appositi rivelatori (‘calorimetri’) e misurando l’energia che così si sviluppa. L’identificazione di una particella è generalmente eseguita risalendo alla sua massa dalle misure della quantità di moto e dell’energia, e talvolta osservando il suo decadimento o il suo modo di interagire con la materia (per es., un elettrone di alta energia produce nell’attraversare la materia uno sciame elettromagnetico le cui caratteristiche sono diverse da quelle della catena di interazioni prodotte da un adrone, mentre un muone subisce perdite di energia per ionizzazione).
Le proprietà delle particelle
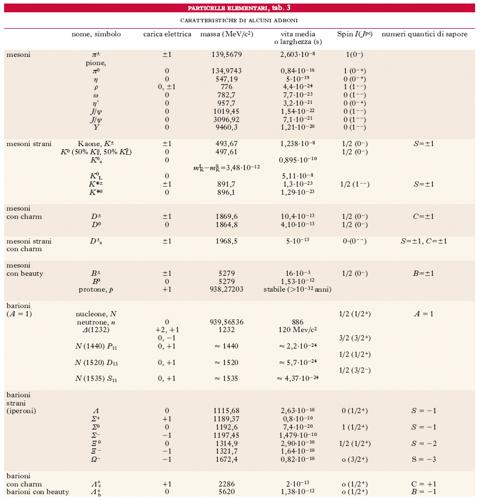
Famiglie di particelle. - Oltre alle particelle fondamentali elencate nella tab. 2 (bosoni di gauge, quark e leptoni), è utile considerare la vastissima famiglia degli adroni, le particelle subnucleari costituite da quark, e soggette a interazione forte. Alcuni delle varie centinaia di adroni sono elencati nella tab. 3; sono distinti in mesoni (gli adroni a spin intero) e barioni (a spin semintero).
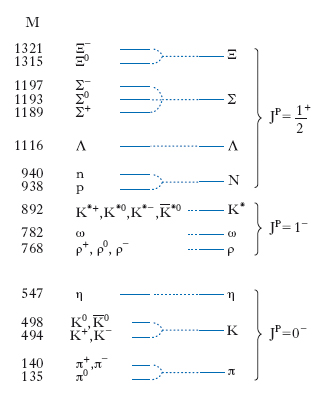
Riportando (fig. 2) i valori delle masse degli adroni sotto forma di trattini orizzontali, secondo uno schema simile a quello usualmente impiegato per rappresentare i livelli energetici di un atomo o di un nucleo, la cosa che maggiormente colpisce è l’esistenza di multipletti di massa, ossia adroni con diversa carica elettrica le cui masse differiscono molto poco fra loro. Usando la terminologia spettroscopica, si esprime questa osservazione dicendo che in natura esistono singoletti, doppietti, tripletti ecc. di massa e che i termini di uno stesso multipletto si distinguono per il valore della carica elettrica. Questi multipletti si interpretano estendendo a tutti gli adroni il concetto di spin isotopico o isospin, introdotto per la prima volta nel caso del protone e del neutrone, i quali sono considerati due diversi stati (di carica) di un’unica particella, il nucleone. I vari multipletti di massa a loro volta formano dei supermultipletti (ottetti, decupletti ecc.), gruppi di adroni con caratteristiche analoghe, anche se le loro masse differiscono in misura molto maggiore che all’interno di un multipletto. La proliferazione degli adroni e l’affiorare di queste regolarità hanno costituito all’inizio degli anni 1960 il punto di partenza delle ricerche teoriche e sperimentali che hanno portato a riconoscere negli adroni sistemi composti da particelle più piccole e alla formulazione del modello a quark.
Attributi delle particelle. - Nelle tab. 2 e 3 sono indicati, oltre ai valori della carica elettrica e della massa, anche quelli di altre grandezze che caratterizzano le particelle elencate.
La carica elettrica q di tutte le particelle a eccezione dei quark risulta pari a un multiplo intero (piccolo o nullo) della carica posseduta (con segno opposto) dal protone e dall’elettrone (pari a 1,60217733∙10−19C) che è quindi assunta come unità di misura.
La massa riportata è la massa a riposo (o di quiete) M espressa in MeV/c2 (1MeV/c2=1,78266270•10−30 kg); molto spesso, invece del valore della massa, viene dato quello dell’energia di quiete Mc2, con c velocità della luce nel vuoto.
Altra proprietà notevole di ogni particella è la sua vita media τ, l’intervallo di tempo (misurato nel sistema di riferimento in cui la particella è in quiete) che in media trascorre prima che la particella decada; cioè se si osserva una particella in quiete per un intervallo di tempo t, la probabilità che essa decada in questo intervallo è pari a 1−exp(−t/τ). Una determinata particella può in via generale decadere attraverso diversi processi alternativi o ‘modi di decadimento’, con probabilità o frequenze caratteristiche di ciascuno di essi.
Le p. posseggono inoltre un momento della quantità di moto intrinseco o spin, proprietà che le rende in qualche modo simili a microscopici giroscopi. Se si prende come unità di misura di questa grandezza la costante di Planck ridotta ℏ=h/2π=1,05457266∙10−34J∙s, lo spin risulta sempre uguale a un numero intero (o nullo) oppure a un numero semintero (1/2, 3/2 ecc.); esso viene di solito indicato con la lettera J ed è uno dei numeri quantici che caratterizzano le particelle elementari.
Una relazione fondamentale di carattere generale stabilisce che tutte le particelle con spin semintero seguono la statistica di Fermi-Dirac e vengono pertanto indicate come fermioni, mentre tutte le particelle dotate di spin intero (o nullo) obbediscono alla statistica di Bose-Einstein e vengono indicate come bosoni. Si tratta di categorie di oggetti con proprietà molto diverse descritti da funzioni d’onda con proprietà di simmetria peculiari. Come accennato, gli adroni sono suddivisi in base allo spin in mesoni e barioni: i mesoni, il più leggero dei quali è il pione, sono bosoni; i barioni, il più leggero dei quali è il nucleone, sono fermioni.
Ogniqualvolta lo spin J e la carica elettrica q di una particella sono diversi da zero essa possiede un momento magnetico parallelo alla direzione dello spin, proprio come ci si attenderebbe dal punto di vista classico per un corpuscolo carico ruotante su sé stesso. Secondo la meccanica quantistica, il valore del momento magnetico di una particella con spin 1/2 priva di struttura dovrebbe essere, a meno di correzioni dell’ordine dell’1‰, μ=qh/4πMc (magnetone, che in unità SI si esprime come μ=μ0qh/4πM). Sono stati misurati con grande precisione i momenti magnetici di elettrone e muone, che sono risultati in perfetto accordo con i valori previsti dall’elettrodinamica quantistica; quelli dei barioni dotati di una vita media abbastanza lunga sono risultati diversi, anche di un fattore 2, dal valore del magnetone nel caso di barioni carichi e diversi da zero (e dello stesso ordine di grandezza del momento magnetico dei barioni carichi) nel caso dei barioni neutri. Il fatto che i barioni sono dotati di momenti magnetici anomali è una chiara indicazione di una loro struttura interna.
Antiparticelle. - Per ogni particella esiste una corrispondente antiparticella, caratterizzata dall’avere rigorosamente la stessa massa, la stessa vita media e lo stesso spin, carica elettrica e momento magnetico rigorosamente uguali in valore assoluto ma di segno opposto; essa viene indicata con lo stesso simbolo della corrispondente particella, sopra il quale è tracciata una lineetta (a eccezione dei leptoni carichi e−, μ−, τ−, le cui antiparticelle sono indicate con e+, μ+, τ+). L’esistenza di antiparticelle, prevista da Dirac nel caso dei fermioni a spin 1/2, fu confermata sperimentalmente con la scoperta del positrone (1932), dell’antiprotone (1955), dell’antineutrone (1956), e successivamente con la scoperta di numerosissime altre antiparticelle. Nel caso dei fermioni, la produzione di un’antiparticella è necessariamente associata a quella di una particella (coppia particella-antiparticella). Come si vedrà più avanti, l’esistenza delle antiparticelle è connessa a una particolare operazione di simmetria, detta coniugazione di carica.
Le interazioni fondamentali. - Una caratteristica fondamentale di ogni particella è costituita dalla natura delle forze con cui essa interagisce con altre particelle subnucleari, caratteristica che, come abbiamo veduto, fornisce il primo criterio per la classificazione delle particelle stesse; per quanto riguarda le interazioni gravitazionali, sebbene siano estremamente importanti alla scala dei fenomeni macroscopici (in particolare alla scala dei fenomeni astrofisici e cosmologici), tuttavia, a causa della piccolezza delle masse in gioco, esse non danno luogo ad alcun fenomeno osservabile nell’ambito delle particelle subnucleari, almeno alle energie oggi accessibili; pertanto, nel seguito, saranno completamente trascurate.
Le interazioni elettromagnetiche, aventi raggio di azione infinito, si esercitano tra particelle dotate di carica elettrica; in particolare mantengono gli elettroni legati ai nuclei per formare gli atomi.
Le interazioni forti, aventi intensità molto maggiore di quelle elettromagnetiche (e corto raggio di azione a livello degli adroni), si esercitano tra tutte le particelle a esclusione del fotone, dei bosoni intermedi W± e Z e dei leptoni; in particolare legano tra loro i protoni e i neutroni per formare i nuclei (per questo erano dette in passato forze nucleari).
Le interazioni deboli, aventi cortissimo raggio d’azione e intensità molto minore di quelle elettromagnetiche, si esercitano tra tutte le particelle a eccezione del fotone e dei gluoni; in particolare sono responsabili della disintegrazione di molte particelle (neutrone, pioni carichi, muone ecc.) e giocano un ruolo fondamentale nelle reazioni nucleari che hanno luogo nelle stelle.
Particelle stabili e instabili. - In base alla vita media le particelle subnucleari sono divise in stabili, quasi stabili e instabili. Le particelle stabili sono quelle delle quali non è mai stato osservato il decadimento e per le quali si può quindi ritenere che la vita media sia infinita ovvero estremamente grande. Le particelle quasi stabili, pur decadendo spontaneamente in altre particelle, hanno una vita media sufficientemente lunga da poter percorrere, prima di decadere, un tratto osservabile sperimentalmente. Le particelle instabili (o risonanze) sono particelle che hanno una vita media così breve che, anche quando viaggiano a velocità confrontabili con quella della luce nel vuoto subendo la dilatazione relativistica del tempo, percorrono sempre tratti troppo piccoli per poter essere osservati. Questo diverso comportamento è dovuto al fatto che per le particelle quasi stabili il decadimento è determinato dalle interazioni deboli (n, μ, π± ecc.) o dalle interazioni elettromagnetiche (π0, η ecc.), mentre per quelle instabili è in genere determinato dalle interazioni forti; come regola qualitativa si può dire infatti che, a parità di condizioni cinematiche, più è intensa l’interazione che determina il decadimento, più è breve la vita media. Senza entrare nei dettagli, malgrado il valore brevissimo della vita media (anche 10−24 s), massa e vita media di particelle instabili possono essere determinate con ottima precisione. Alle masse si risale da misure di quantità di moto ed energia di tutti i corpuscoli prodotti nel decadimento. Alla vita media dall’analisi della sezione d’urto dei processi in cui sono prodotte particelle instabili.
Numeri quantici che caratterizzano le particelle
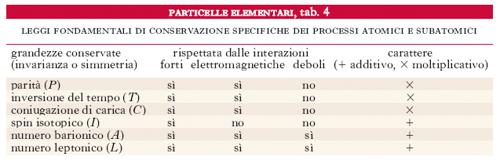
Leggi di conservazione. - Lo studio sistematico dei processi che hanno luogo nell’ambito delle p. ha permesso di riconoscere che essi si svolgono rispettando certe leggi di conservazione. Di queste, alcune sono le stesse che valgono per un sistema macroscopico isolato (conservazione della quantità di moto, dell’energia, del momento della quantità di moto, della carica elettrica), mentre altre sono specifiche dei fenomeni atomici e subatomici. Ogni legge di conservazione è connessa a una corrispondente proprietà di simmetria; le leggi di conservazione della quantità di moto e dell’energia vanno intese in forma relativistica, cosicché la seconda di queste comprende anche l’energia di quiete delle particelle. Dal punto di vista quantistico, ad alcune delle grandezze conservate corrisponde un numero quantico discreto: così, per es., nel caso di una singola particella in quiete, il momento della quantità di moto è espresso (in unità di ℏ/2π) da un ben determinato valore intero o semintero dello spin J.
Tuttavia, queste grandezze e i corrispondenti numeri quantici si possono comportare in due modi sostanzialmente diversi quando si considerano sistemi composti di due o più sistemi parziali. Alcuni, come il momento della quantità di moto, sono additivi (in questo caso vettorialmente) e sono indicati nella tab. 4 con il simbolo +, mentre altri, come la parità, sono moltiplicativi e sono indicati con il simbolo ×. Mentre alcune delle leggi di conservazione elencate nella tab. 4 sono di validità generale, altre sono rispettate da alcune ma non da tutte le tre interazioni fondamentali che interessano le particelle subnucleari.
Parità intrinseca. - Il concetto di parità di un sistema in un ben determinato stato, si ricollega al comportamento della corrispondente funzione d’onda ψ(x,y,z,t,Jz), quando a questa viene applicata l’operazione di parità, P, consistente nell’invertire il verso degli assi x, y, z, lasciando invariato il verso di scorrimento del tempo t. Questa operazione fa passare da una terna di riferimento destra a una terna sinistra (o viceversa). Per ogni stato di un sistema si può definire uno stato speculare che è connesso allo stato originario, come l’immagine di un oggetto prodotta per riflessione nell’origine è connessa all’oggetto stesso. Poiché, d’altra parte, l’applicazione per due volte successive dell’operazione di parità deve lasciare la funzione d’onda ψ(x,y,z,t,Jz) invariata, ne segue che, per uno stato con simmetria speculare, cioè per un autostato della parità, deve necessariamente verificarsi l’uno o l’altro dei 2 seguenti casi:
Si dice allora che lo stato considerato ha una parità ben definita, e più precisamente che ha parità pari, o +1, o semplicemente +, nel primo caso, che ha parità dispari, o −1, o semplicemente −, nel secondo. La parità di una particella in un determinato stato a parità definita si può scindere nel prodotto della parità della funzione d’onda che descrive il suo moto (parità orbitale), per la parità intrinseca del corpuscolo stesso. Mentre la parità della funzione d’onda che descrive il moto di una singola particella (o il moto relativo di 2 particelle) è data dalla semplice formula P=(−1)l, dove l è il valore del momento della quantità di moto cosiddetto orbitale (espresso in unità di ℏ/2π), la parità intrinseca è una proprietà (intrinseca) della particella: il suo valore è determinato purché si convenga di assumere come uguale a +1 la parità intrinseca di una particella scelta arbitrariamente: per es., la parità del protone. In queste condizioni, la parità delle altre particelle può essere stabilita sperimentalmente grazie alla legge di conservazione che afferma che, in tutti i processi in cui intervengono solo interazioni forti e interazioni elettromagnetiche, la parità dello stato finale, Pf, è sempre uguale alla parità dello stato iniziale Pi. Poiché la parità è un numero quantico moltiplicativo, sia Pf sia Pi sono date dal prodotto delle parità intrinseche delle varie particelle e della parità della funzione d’onda che descrive il loro moto relativo.
Fino al 1957 si riteneva che la legge di conservazione della parità dovesse valere in modo del tutto generale, ovvero per tutte le interazioni, in quanto essa deriva dall’ipotesi, plausibile, che i fenomeni elementari siano tali da non permettere di distinguere, se non con una nostra scelta arbitraria, una terna di assi destrorsa da una sinistrorsa. Ma nel 1957 fu scoperto che i processi che hanno luogo tramite le interazioni deboli non rispettano questa legge, mentre essa è rigorosamente valida nel caso di processi dovuti a interazioni forti e interazioni elettromagnetiche. Nel caso dei leptoni (che sono prodotti o mediante interazioni elettromagnetiche in coppia particella-antiparticella o mediante interazioni deboli e che decadono tramite processi deboli, che non conservano la parità) la parità non è definita e pertanto essa non figura fra i loro numeri quantici caratteristici.
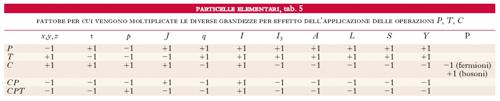
Inversione del tempo e coniugazione di carica. - Accanto all’operazione di parità P, si debbono considerare altre due operazioni di simmetria in qualche modo analoghe a P. La prima, indicata con T e detta inversione del tempo (➔ tempo), è connessa con la proprietà delle equazioni della dinamica classica di rimanere invariate quando si inverte il verso dell’asse dei tempi; la seconda, indicata con C e detta coniugazione di carica, è connessa con la simmetria dei fenomeni rispetto alle cariche elettriche dei due segni. Quest’ultima legge di simmetria non sembrava essere rispettata nell’ambito della fisica atomica e nucleare, dato che le particelle dotate di carica negativa (gli elettroni) sono molto più leggere di quelle dotate di carica positiva (i protoni e i nuclei) e che protoni e neutroni non posseggono cariche uguali e opposte. Ma la scoperta dell’elettrone positivo, dell’antiprotone e in generale delle antiparticelle ha portato a ristabilire la validità di questa proprietà di simmetria. Le operazioni T e C vengono applicate, al pari di P, alle funzioni d’onda che descrivono gli stati di un sistema (tab. 5). Si dice che un processo fra p. ubbidisce alla legge dell’invarianza rispetto all’inversione del tempo se il processo che si ottiene applicando l’operazione T (ossia cambiando il segno di tutti gli spin e di tutte le quantità di moto e scambiando contemporaneamente le quantità di moto iniziali e finali) ha luogo in natura come quello originario. L’operazione di coniugazione di carica C non solo cambia il segno della carica delle particelle ma anche il segno di tutti gli altri numeri quantici interni (numero barionico A, numero leptonico L, stranezza S, e ipercarica Y). L’esperienza ha mostrato che la legge di invarianza per coniugazione di carica è rispettata in tutti i processi che hanno luogo tramite le interazioni forti ed elettromagnetiche ma non in quelli dovuti alle interazioni deboli.
Teorema CPT. - Sotto ipotesi molto generali si dimostra nella teoria dei campi relativistici quantizzati che tutti i processi debbono essere invarianti rispetto alla operazione CPT, consistente nell’eseguire una dopo l’altra le 3 operazioni T, P, C (teorema CPT). Da questo teorema, tra l’altro, discende che la massa e la vita media di una particella debbono essere eguali a quelle della corrispondente antiparticella. Poiché si è osservato sperimentalmente nel decadimento dei kaoni neutri che le interazioni deboli non rispettano neppure l’invarianza rispetto a CP, segue, sempre dal teorema CPT, che queste interazioni (a differenza di quelle forti ed elettromagnetiche) non rispettano l’invarianza rispetto a T. La violazione di CP, anche se estremamente piccola, potrebbe spiegare l’asimmetria tra materia e antimateria osservata nell’Universo.
Numero barionico. - Dall’esame sistematico dei dati sperimentali è risultato che valgono altre 2 leggi di conservazione, ciascuna delle quali ha portato alla definizione di un nuovo numero quantico di importanza fondamentale per la classificazione delle particelle elementari. Senza alcuna eccezione, tutti i processi osservati fino a oggi si svolgono rispettando la legge di conservazione del numero barionico. Questo non è altro che una generalizzazione del numero di massa A; si tratta di una grandezza additiva che viene presa pari a +1 per il protone, il neutrone e per qualsiasi altro barione, uguale a −1 per le corrispondenti antiparticelle e uguale a zero per tutte le altre particelle, cioè per i mesoni, i leptoni e i bosoni di gauge. Si può allora affermare che in tutti i processi fra p. la somma algebrica dei numeri barionici Aj delle particelle presenti nello stato finale è uguale alla somma algebrica dei numeri barionici Ai delle particelle presenti nello stato iniziale.
Numero leptonico. - Una legge analoga vale anche per i leptoni: se si attribuisce a ciascun leptone un numero leptonico L=+1, a ciascun antileptone un numero leptonico L=−1 e a tutte le altre p. un numero leptonico L=0, tutti i processi finora osservati, senza eccezione, seguono la legge di conservazione del numero leptonico: in qualsiasi processo la somma algebrica dei numeri leptonici Lj delle particelle presenti nello stato finale è sempre uguale alla somma algebrica dei numeri leptonici delle particelle presenti nello stato iniziale Li. Sperimentalmente si è anzi osservato che la legge di conservazione del numero leptonico può essere ulteriormente precisata: attribuendo a elettrone e neutrino-e numero (leptonico) ‘elettronico’ Le=+1 (−1 alle loro antiparticelle e zero a tutte le altre particelle), a muone e neutrino-μ numero (leptonico) ‘muonico’ Lμ=+1 (−1 alle loro antiparticelle e zero a tutte le altre particelle), a tauone e neutrino-τ numero (leptonico) ‘tauonico’ Lτ=+1 (−1 alle loro antiparticelle e zero a tutte le altre particelle), risulta che in tutte le interazioni è conservato ciascuno di questi numeri.
Spin isotopico. - Come si è accennato, l’esistenza dei multipletti di massa (fig. 2) suggerisce l’idea che gli adroni appartenenti allo stesso multipletto debbano essere considerati come diversi stati di una stessa particella; da questo punto di vista, per es., il protone e il neutrone costituiscono i due stati di un doppietto, il nucleone; analogamente il π+, il π0 e il π− costituiscono esempi di tripletti, indicati semplicemente come π e Σ, mentre Λ è un singoletto, cioè la sola particella neutra Λ0. I membri di uno stesso multipletto, oltre ad avere approssimativamente la stessa massa, hanno sempre lo stesso spin J e la stessa parità P, che vengono per convenzione scritti nella forma JP; essi differiscono invece uno dall’altro per il valore della carica elettrica. In analogia con quanto si fa nello studio del nucleo per interpretare la molteplicità dei corrispondenti livelli, si associa a ciascun multipletto un operatore vettoriale I, lo spin isotopico o isospin (spesso indicato in fisica nucleare col simbolo T), il quale gode, in uno spazio rappresentativo astratto, detto isospazio, di proprietà matematiche analoghe a quelle di cui gode nello spazio ordinario l’operatore vettoriale J che rappresenta lo spin di un sistema. In particolare, come il vettore J può avere 2J+1 orientamenti tali che la sua componente Jz lungo l’asse z assuma i valori J, J−1, J−2, ..., −J, così la terza componente I3 di I può assumere solo i 2I+1 valori I, I−1, I−2, ..., −I, ciascuno dei quali individua un diverso membro del multipletto di spin isotopico. Il corrispondente valore della carica elettrica q, misurata in unità e, dipende solo dal valore di I3 ed è dato da
Così, per es., nel caso del nucleone si ha JP=1/2+, A=1, I=1/2. Si tratta di un doppietto, dato che 2I+1 = 2; e poiché I3 ha i due soli valori ±1/2, i membri del doppietto hanno carica q rispettivamente pari a +1 e 0 e corrispondono rispettivamente al protone e al neutrone. Si è inoltre osservato sperimentalmente che tutti i processi in cui intervengono solo interazioni forti si svolgono sempre in modo che non solo la carica elettrica e il numero barionico (e quindi I3) ma anche I abbia nello stato finale lo stesso valore che ha nello stato iniziale. Questa legge di conservazione viene spesso espressa dicendo che le interazioni forti sono indipendenti dalla carica elettrica, o, ciò che è lo stesso, che le interazioni forti, quando si trascurano le differenze di massa all’interno di ogni multipletto, sono invarianti rispetto alle rotazioni nello spazio rappresentativo dello spin isotopico. Si deve insistere sul fatto che la legge sopra enunciata vale solo per le interazioni forti, non per le interazioni elettromagnetiche, le quali ovviamente dipendono in modo essenziale dal valore della carica e quindi da I3: si può pensare che esse siano responsabili della piccola separazione fra i vari termini di uno stesso multipletto di massa. Questi sono ‘degeneri’ (cioè dotati della stessa energia) fintanto che si trascura l’interazione elettromagnetica, la quale costituisce una piccola perturbazione che toglie la degenerazione. Anche le interazioni deboli non rispettano la conservazione dello spin isotopico; ne segue che per i leptoni, i quali presentano solo interazioni deboli ed elettromagnetiche, e per il fotone, che possiede solo l’interazione elettromagnetica, il concetto di spin isotopico perde significato.
Stranezza, ipercarica e altri numeri quantici di ‘sapore’. - M. Gell-Mann e K. Nishijima introdussero indipendentemente nel 1953 un nuovo numero quantico additivo, chiamato stranezza (S), per spiegare il fatto ‘strano’ che le particelle scoperte nel 1947 fra i corpuscoli secondari della radiazione cosmica (cioè la Λ e il K°) decadono troppo lentamente rispetto all’abbondanza con cui sono prodotte. Essi enunciarono inoltre la legge della conservazione della stranezza: in un processo in cui intervengono solo interazioni forti ed elettromagnetiche, la somma algebrica delle stranezze delle particelle presenti nello stato finale è sempre uguale alla somma algebrica delle stranezze nello stato iniziale. La stranezza non si conserva invece nelle interazioni deboli e quindi in tutti i decadimenti delle particelle strane che sono dovuti proprio a queste interazioni. La stranezza di una particella veniva definita modificando l’espressione che fornisce la carica elettrica nel seguente modo:
questa relazione veniva scritta anche nella forma:
,
avendo introdotto l’ipercarica Y=A+S, e si riduceva evidentemente a quella trovata precedentemente per tutte le p. dotate di stranezza nulla (S=0). Per caratterizzare nuove particelle e il loro comportamento sono stati successivamente introdotti ulteriori numeri quantici additivi: il fascino o charm C, la bellezza o beauty o bottomness B, la verità o truth o topness T (detti con la stranezza numeri quantici di sapore, in inglese flavour), conservati nelle interazioni forti ed elettromagnetiche ma non nelle deboli, che compaiono nell’espressione che fornisce la carica elettrica di una particella alla stessa stregua della stranezza. Oggi si sa che la stranezza rappresenta il contenuto in quark s di un adrone: ovvero la stranezza è data da S=ns̄ − ns, dove ns,s̄ è il numero di quark s o di antiquark s̄ nell’adrone. Analogamente i nuovi numeri quantici di sapore C, B, T sono collegati al contenuto in quark c, b, t, di un adrone. Come la carica elettrica, il numero barionico e il numero leptonico, così anche la stranezza e gli altri numeri quantici di sapore cambiano di segno quando si passa da una particella alla corrispondente antiparticella.
Caratteristiche del Modello Standard
Negli anni 1960, dallo studio sistematico dei supermultipletti adronici ai quali si è accennato precedentemente, è emerso che gli adroni sono stati legati di costituenti più semplici con spin 1/2, carica elettrica e numero barionico frazionari, i quark; questa ipotesi è stata successivamente convalidata da numerose evidenze sperimentali indipendenti. Le principali caratteristiche dei quark sono riportate in tab. 2. Di conseguenza, il problema di inquadrare teoricamente le particelle che danno luogo a interazioni forti si è spostato dall’ambito degli adroni composti a quello dei quark componenti. Negli anni 1970 il problema delle interazioni forti è stato impostato nella cornice concettuale della cromodinamica quantistica (QCD) che è la teoria di campo delle interazioni tra i quark e i gluoni dotati della cosiddetta carica di colore (conservata) che svolge nelle interazioni forti un ruolo analogo alla carica elettrica nelle interazioni elettromagnetiche. Nello stesso periodo si è sviluppata la teoria unificata delle interazioni elettrodeboli tra i quark, i leptoni e un certo numero di bosoni che mediano le forze. Tutte le conoscenze teoriche e sperimentali acquisite sulle p. trovano coerente sistemazione in quello che viene detto Modello Standard delle particelle fondamentali e delle loro interazioni, che comprende la cromodinamica quantistica e la teoria elettrodebole.
Nel Modello Standard sono assunti come fondamentali 12 fermioni con spin 1/2 (i 6 leptoni e i 6 quark, ciascun quark in 3 repliche con diversa carica di colore) e i 12 bosoni di gauge con spin 1 (il fotone, i bosoni W±, Z e gli otto gluoni ‘colorati’) che mediano le interazioni elettrodeboli e forti tra i fermioni. Le interazioni sono descritte da teorie di campo con invarianza di gauge non abeliana (➔ deboli, interazioni). Gli adroni sono costituiti da 3 quark (i barioni) o da un quark e un antiquark (i mesoni) legati dallo scambio di gluoni che hanno massa e carica elettrica nulle. Mentre i quark possiedono carica di colore, gli adroni ne sono globalmente privi e le interazioni forti tra adroni sono interazioni ‘residue’ dovute allo scambio di composti neutri rispetto al colore, cioè di altri adroni per lo più leggeri, in particolare pioni e altri mesoni. Il confinamento dei quark negli adroni, cioè l’impossibilità di avere quark liberi, è riconducibile al fatto che possono sussistere come stati liberi solo p. prive di colore.
I fermioni fondamentali vengono raggruppati in tre famiglie o generazioni, ciascuna contenente due tipi o sapori di quark e due leptoni:
La somma delle cariche elettriche delle p. appartenenti a ciascuna famiglia è zero poiché il neutrino ha carica 0, il leptone carico ha carica −1, e i quark 3∙(2/3) e 3∙(−1/3): il fattore 3 è dovuto al fatto che di ogni quark vi sono 3 repliche con diversa carica di colore. Le masse delle p. appartenenti a una famiglia (con l’eccezione dei neutrini che potrebbero avere tutti massa zero) crescono passando da una famiglia alla successiva. La prima famiglia ha un ruolo particolare perché tutta la materia che ci circonda coinvolge solo i fermioni di questa generazione: ciò perché i membri della seconda e terza famiglia (con l’eccezione dei neutrini) sono instabili e quindi, dopo aver avuto un ruolo importante nell’Universo primordiale, negli istanti immediatamente successivi al big-bang, sono oggi presenti solo in eventi di alta energia prodotti dalla radiazione cosmica o dalle macchine acceleratrici. Misure estremamente precise della larghezza della distribuzione di massa del bosone Z eseguite a partire dal 1989 con il LEP, il grande anello di collisione per elettroni e positroni del CERN, hanno mostrato che esistono solo 3 specie di neutrini (con massa nulla o comunque all’incirca minore di metà della massa dello Z) e quindi solo 3 famiglie di fermioni fondamentali. Le ragioni di questa triplice replica dei fermioni fondamentali rappresentano uno degli aspetti più misteriosi della attuale fisica delle particelle.
I leptoni di ciascuna famiglia, (νe, e), (νμ, μ), (ντ, τ) costituiscono un doppietto del cosiddetto isospin debole T e non possono trasformarsi in quelli di un’altra (possono solo trasformarsi l’uno nell’altro per emissione o assorbimento di un bosone carico W±).
I quark di ciascuna famiglia (u,d), (c,s), (t,b), tutti con masse definite e diverse tra loro, non costituiscono invece doppietti di isospin debole e possono trasformarsi in quelli di un’altra: è però possibile costruire 3 combinazioni lineari d′, s′, b′, dei quark d, s, b, con carica elettrica −1/3 (oppure di quelli con carica 2/3) in modo che le interazioni deboli tra quark mediate da un bosone carico W± abbiano luogo sempre e soltanto nell’ambito di una delle coppie (u,d′), (c,s′), (t,b′), che costituiscono dei doppietti di isospin debole. Nello studio delle interazioni deboli si raggruppano quindi i fermioni fondamentali in tre famiglie o generazioni come quelle sopra riportate, ma con d′, s′, b′ al posto di d, s, b. I campi elettrodebole e forte (o di colore) responsabili delle interazioni tra i fermioni fondamentali sono costruiti sulla falsariga del campo elettromagnetico (➔ elettrodinamica) imponendo l’invarianza di gauge. Poiché i fermioni fondamentali, sorgenti dell’interazione elettrodebole, costituiscono dei doppietti di isospin debole, una trasformazione di gauge della loro funzione d’onda è individuata da tre parametri reali, che identificano una matrice speciale unitaria 2 × 2, più un parametro associato a una trasformazione di fase indipendente, che serve per unificare correttamente le interazioni elettromagnetiche e deboli; per assicurare l’invarianza di gauge locale tali parametri debbono essere funzioni arbitrarie dello spazio-tempo; come nell’elettromagnetismo, a ognuna di queste funzioni corrisponde un campo vettoriale: uno, il cui quanto è indicato con W°, dà luogo a interazioni che non causano cambiamenti di T3; due causano transizioni tra gli stati T3=1/2 e T3 = −1/2 dei fermioni, e i loro quanti sono indicati con W+ e W−; il quarto campo è associato alla trasformazione di fase indipendente e il suo quanto è indicato con B°. Il fotone e lo Z sono una miscela dei quanti elettricamente neutri B° e W°. I quanti associati ai campi di gauge (bosoni di gauge) debbono avere massa uguale a zero come il fotone; la massa molto elevata dei bosoni W± e Z è attribuita alla rottura spontanea della simmetria di gauge mediante il cosiddetto meccanismo di Higgs, per cui devono intervenire i bosoni di Higgs (➔ bosone). Poiché i quark, sorgenti delle interazioni forti, sono dei tripletti di colore, una trasformazione di gauge della loro funzione d’onda è descritta da una matrice speciale unitaria 3 × 3 e quindi da 8 parametri reali che per assicurare l’invarianza locale di gauge debbono essere funzioni arbitrarie dello spazio-tempo: a ciascuna di queste funzioni corrisponde un campo vettoriale e il relativo quanto (gluone). Come nell’elettromagnetismo, nel Modello Standard tutti gli accoppiamenti dei fermioni hanno la forma di un prodotto scalare tra una corrente (che descrive il trasporto di carica elettrica o di isospin debole o di colore) e un campo vettoriale.
Un’importante conferma del Modello Standard è stata fornita nel 1995 dalla definitiva verifica sperimentale dell’esistenza del quark t; un’ancor più significativa conferma potrà avvenire con la rivelazione di almeno un bosone di Higgs neutro con spin zero (è questo l’obiettivo principale delle ricerche condotte con il collisionatore LHC, inaugurato al CERN nel 2008).
Le teorie di ‘Grande Unificazione’
Nel Modello Standard non vi è alcuna relazione tra le interazioni elettrodebole e forte: sono allo studio teorie cosiddette di ‘Grande Unificazione’ che prevedendo transizioni quark-leptone dovrebbero correlare dette interazioni. Una diretta estrapolazione del Modello Standard suggerisce fortemente l’unificazione delle forze: le intensità delle interazioni forti, deboli ed elettromagnetiche, che sono molto differenti alle energie che caratterizzano i fenomeni che ci circondano, tendono a convergere verso un unico valore che dovrebbe essere raggiunto a energie dell’ordine di 1015 GeV; le interazioni che appaiono diverse alle energie oggi accessibili potrebbero scaturire da una teoria unificata basata su una più estesa simmetria tra quark e leptoni. Le interazioni responsabili delle transizioni tra quark e leptoni, che comportano la violazione della conservazione sia del numero barionico sia di quello leptonico e la conseguente instabilità del protone (la cui vita media risulta sperimentalmente maggiore di 1032 anni), sarebbero alle energie sin qui esplorate del tutto trascurabili perché mediate da quanti di massa enorme, dell’ordine appunto di 1015 GeV/c2, ovvero tali interazioni divengono importanti a distanze dell’ordine di 10−31 m. A distanze ancora più piccole il Modello Standard deve necessariamente essere ampliato. Infatti gli effetti della gravità divengono non trascurabili a distanze dell’ordine di 10−35 m, ma non esiste ancora una teoria consolidata della gravità quantistica. Il Modello Standard, che tratta i fermioni fondamentali come puntiformi, fornisce una interpretazione coerente e una descrizione dei fenomeni che coinvolgono le p. che risulta sperimentalmente corretta fino a distanze dell’ordine di 10−18 m.
Una questione aperta di grande interesse in fisica delle particelle è se il Modello Standard rappresenti una descrizione delle interazioni fondamentali valida fino alle distanze caratteristiche della Grande Unificazione o addirittura fino al limite ove gli effetti microscopici della gravità non possono più essere trascurati (10−35 m). In altre parole ci si domanda se con la scoperta del bosone di Higgs si potrà considerare chiuso il capitolo della fisica delle interazioni fondamentali per tutte le energie direttamente accessibili agli esperimenti con gli acceleratori. Secondo il punto di vista di gran lunga prevalente è molto improbabile che il Modello Standard risulti valido fino alle distanze caratteristiche della Grande Unificazione, ed è ragionevole invece aspettarsi di trovare nuovi fenomeni fisici a energie dell’ordine del TeV. Infatti, vi è un problema di stabilità della teoria rispetto alle fluttuazioni quantistiche legato alle divergenze tipiche delle teorie con campi fondamentali scalari (come i campi di Higgs).
Supersimmetria
Una possibile classe di soluzioni estende il Modello Standard introducendo per ogni stato fermionico un corrispondente stato bosonico, con gli stessi numeri quantici interni, e viceversa. Il modello viene così dotato di una simmetria bosone-fermione che è chiamata supersimmetria. Nel limite simmetrico le divergenze dovute ai bosoni si cancellano esattamente e il risultato è lo stesso che in una teoria con soli fermioni. Naturalmente la supersimmetria deve essere rotta, perché i partner supersimmetrici delle particelle note non sono stati osservati: l’ordine di grandezza delle loro masse dovrebbe essere non più di qualche TeV/c2 perché la teoria riproduca correttamente la grandezza osservata delle masse del W e dello Z. Il Modello Standard esteso con la supersimmetria è una teoria ben definita che non presenta per il momento problemi circa l’accordo con l’esperimento. Inoltre la supersimmetria è un ingrediente molto importante delle attuali teorie della gravità quantistica, e quindi, in qualche modo, il suo ruolo a basse energie potrebbe essere collegato alla teoria unificata di tutte le interazioni, inclusa la gravità. Gli esperimenti programmati per i prossimi decenni verificheranno l’effettiva esistenza delle p. supersimmetriche.
Abstract di approfondimento da Particelle elementari di Nicola Cabibbo (Enciclopedia della Scienza e della Tecnica)
Introduzione
La materia presenta una gerarchia di strutture: i corpi sono composti da molecole, le molecole da atomi, gli atomi da elettroni che orbitano intorno a un nucleo, il nucleo da protoni e neutroni, che, a loro volta, sono composti da quark. Per quanto ne sappiamo oggi, elettroni e quark sono privi di una struttura interna e sono quindi considerati ‘elementari’. Lo studio delle particelle muove dal grande verso il piccolo, ma ogni acquisizione in questo campo si riflette all’indietro fornendo una solida base alla comprensione delle strutture più grandi e più complesse: le proprietà degli atomi sono basate su quelle degli elettroni e dei nuclei, e le proprietà dei nuclei derivano in ultima analisi dal comportamento dei quark che li compongono e dalle loro interazioni. Detto questo, è bene ricordare che la trattazione matematica di sistemi complessi – che potremmo definire come i sistemi composti da molte parti in interazione tra loro – diviene rapidamente assai difficile al crescere del numero dei componenti. Dato che non siamo in grado di derivare esattamente le proprietà degli atomi o dei nuclei a partire dai principî primi, cioè dal comportamento dei loro componenti elementari, dobbiamo ricorrere a semplificazioni concettuali che, pur basate su leggi generali, come quelle della meccanica quantistica, sono specifiche dei rispettivi campi di studio, la fisica atomica e la fisica nucleare.
Non è possibile comprendere, nel dettaglio, il comportamento di un sistema veramente complesso, come per esempio un organismo vivente, nei termini delle particelle che lo compongono. Questo non significa affatto che la conoscenza delle particelle e delle loro interazioni non contribuisca in modo significativo alla comprensione dei sistemi a scala superiore. Per fare un esempio, la fisica delle particelle fornisce fondamentali contributi a campi apparentemente distanti quali l’astrofisica e la cosmologia, tanto da determinare la nascita della nuovissima disciplina delle astroparticelle, che utilizza la fisica delle particelle per la comprensione di fenomeni astrofisici quali la radiazione cosmica o i meccanismi legati all’origine dell’Universo, il big bang. Esempio nell’esempio: l’energia del Sole deriva da reazioni nucleari che si svolgono nella sua zona centrale, e queste reazioni sono accompagnate dall’emissione di neutrini; i recenti risultati ottenuti dallo studio dei neutrini solari hanno permesso una brillante verifica di tali teorie.
Piccole dimensioni e alte energie: gli acceleratori
La natura ondulatoria della luce implica un limite, poco inferiore a 1 mm (51026 m), ai dettagli che possono essere risolti con luce visibile, sia pure con l’ausilio di un microscopio: la lunghezza d’onda della radiazione con cui si illumina un oggetto – circa 0,5 mm per la luce visibile – essenzialmente coincide con la dimensione dei minimi dettagli che una tale radiazione può mettere in evidenza. Per raggiungere dimensioni più piccole occorrono radiazioni di lunghezza d’onda minore; passando dalla luce visibile ai raggi X si ottengono lunghezze d’onda paragonabili alle dimensioni di un atomo, circa 10210 m, e si può esplorare per esempio la struttura delle molecole. La luce è composta da quanti, i fotoni, la cui energia è inversamente proporzionale alla lunghezza d’onda: E5hc/l, dove l è la lunghezza d’onda, c la velocità della luce e h la costante di Planck. Nella luce visibile i fotoni hanno un’energia di circa 1 eV (elettronvolt, l’energia che un elettrone guadagna traversando una differenza di potenziale di un volt), mentre l’energia tipica dei raggi X si misura in migliaia di eV.
Il progresso nello studio di strutture sempre più piccole è indissolubilmente legato alla disponibilità di radiazioni di altissima energia, quindi di piccolissima lunghezza d’onda, in grado di rivelare i dettagli più minuti della struttura del nucleo atomico e dei suoi componenti. I grandi acceleratori di particelle hanno quindi un ruolo centrale negli studi sulle particelle elementari. Le energie sviluppate da queste macchine si misurano in MeV (milioni di eV), GeV (miliardi di eV) e TeV (migliaia di GeV). Mentre la radiazione elettromagnetica, sotto forma di fotoni di altissima energia, ha mantenuto un certo ruolo, si preferiscono attualmente fasci di particelle cariche, come protoni ed elettroni. Secondo la meccanica quantistica anche questi, come i fotoni e del resto tutte le particelle, presentano un aspetto ondulatorio e resta valida la relazione tra energia e potere risolutivo cui abbiamo accennato nel caso dei fotoni. Il grande vantaggio delle particelle cariche è che queste possono essere accelerate mediante campi elettrici e guidate da campi magnetici. Gli acceleratori di particelle si basano sugli stessi meccanismi che permettono il funzionamento dei tubi a raggi catodici nei televisori.
Gli urti tra le particelle e gli anelli di collisione
L’osservazione di un oggetto macroscopico è, con buona approssimazione, un atto neutrale e asimmetrico: la radiazione che illumina e l’oggetto illuminato sono entità ben distinte; inoltre l’illuminazione non modifica l’oggetto osservato. Nello studio delle particelle la situazione è totalmente diversa. Un fascio di particelle (che possono essere fotoni, elettroni, protoni) viene scagliato contro un bersaglio che contiene le particelle che si vogliono studiare. Quello che si osserva è l’effetto degli urti tra singole particelle appartenenti al fascio prodotto da un acceleratore e singole particelle del bersaglio; una situazione totalmente simmetrica tra agente illuminante e oggetto osservato. Inoltre l’urto tra particelle non è affatto un evento neutrale: si tratta di un evento violento che modifica le particelle che vi partecipano. Per effetto dell’urto possono essere create nuove particelle inizialmente non presenti, un fenomeno strettamente connesso all’equivalenza tra energia e massa espressa dalla celebre equazione E5mc2 della relatività di Einstein: parte dell’energia E delle particelle che si scontrano si trasforma nella massa m di nuove particelle.
Sia per ottenere il massimo potere risolutivo, sia per produrre nuove particelle, il parametro che conta è l’energia disponibile nel baricentro delle particelle che si urtano. L’effetto dell’urto è quindi esaltato se, anziché scagliare particelle ad alta energia contro particelle-bersaglio a riposo, si fanno scontrare fasci di particelle che si muovono in direzione opposta, provocando veri e propri scontri frontali. È questo lo schema adottato in molti esperimenti recenti, che fanno uso dei cosiddetti anelli di collisione: si tratta di macchine circolari, nelle quali si realizzano urti tra due fasci di particelle accelerati ad alta energia che si muovono in senso opposto. I due fasci vengono conservati per tempi relativamente lunghi (anche qualche ora) in modo da moltiplicare le occasioni di urto tra le particelle. Un importante progresso per gli anelli di collisione è stato lo sviluppo di macchine in cui si fanno collidere fasci di particelle con fasci delle corrispondenti antiparticelle: elettroni contro positroni, oppure protoni contro antiprotoni. La prima macchina di questo tipo, ADA (Anello di accumulazione), è stata realizzata all’inizio degli anni Sessanta del Novecento nei laboratori dell’Istituto Nazionale di Fisica Nucleare di Frascati, sotto la guida di Bruno Touschek. Da ADA discendono le macchine che hanno fornito i più importanti contributi sperimentali alla fisica delle particelle negli ultimi decenni. La più grande, il LEP (Large electron and positron collider) del CERN di Ginevra, si sviluppava lungo una galleria circolare di 27 km e raggiungeva un’energia di oltre 100 GeV. Recentemente il LEP è stato smontato per far posto a un nuovo anello di collisione, l’LHC (Large hadron collider), che raggiungerà un’energia di 14 TeV nell’urto tra due protoni, un notevole passo avanti nella capacità di scoprire nuove particelle ed esplorare possibili nuove strutture delle particelle che oggi consideriamo elementari.
Abstract di approfondimento da Particelle elementari. Esperimenti di Riccardo Faccini, Fernando Ferroni (Enciclopedia della Scienza e della Tecnica)
Ricerca di nuove particelle
L’enorme successo riscosso dal Modello Standard delle interazioni elementari è stato decretato dal fatto che le sue predizioni teoriche finora hanno trovato sempre conferma. Rimane da spiegare per quale motivo esistano tre famiglie di particelle, e diciannove parametri che assumono proprio i valori misurati; soprattutto, non è stata ancora osservata alcuna particella elementare scalare, in mancanza della quale il modello prevede che tutte le particelle siano prive di massa. Da quando è stata riconosciuta la sua necessità molti esperimenti l’hanno cercata; da ultimo il LEP, che sarebbe stato capace di vedere il bosone di Higgs se esso avesse avuto una massa minore di 115 GeV. Le particelle elementari, secondo il modello di Higgs, acquisiscono massa nell’interazione con il bosone omonimo. Ciò implica che quanto più una particella è pesante, tanto più è probabile che essa emetta tale bosone o che sia prodotta dal suo decadimento.
Come si presenterebbe all’osservazione un bosone di Higgs? Esso decadrebbe nella coppia di corpuscoli dotati di maggior massa tra quelli che gli sarebbero permessi; nell’intervallo di energia del LEP decadrebbe in una coppia di quark bottom. Il principio del confinamento, tuttavia, esclude che possano esistere quark isolati, per cui lo stato finale dovrebbe contenere due mesoni B e numerose altre particelle. Data l’alta energia disponibile e la breve vita media dei mesoni B, il decadimento del bosone di Higgs potrebbe essere riconosciuto dalla presenza di due getti di particelle, alcune provenienti da mesoni B .
In realtà, l’osservazione di un bosone di Higgs non sarebbe sufficiente a completare il modello, che ha gravi limitazioni teoriche: i calcoli necessari a giustificare i valori osservati delle masse appaiono ad hoc, ma tutti i modelli che sono stati sviluppati per cercare di porvi rimedio prevedono l’esistenza di almeno un bosone scalare neutro e di numerose altre particelle; in particolare, la supersimmetria (SUSY) prevede l’esistenza di una replica di tutte le particelle finora note, con le medesime cariche e gli stessi numeri quantici, a parte il momento angolare, e con masse maggiori. Questi modelli prevedono l’esistenza di bosoni di Higgs con carica elettrica non nulla, che decadono prevalentemente in un quark charm e in uno strange, oppure in un leptone t e nel corrispondente neutrino. Simili particelle sono state ricercate invano al LEP e sono l’oggetto d’indagine delle macchine acceleratrici con protoni, il Tevatron al Fermilab e l’LHC al CERN.
Anche gli esperimenti con i mesoni B offrono possibilità di ricerca dei bosoni di Higgs. Da diversi anni si è alla ricerca del decadimento del mesone B2 in un leptone t e nel corrispondente neutrino, che può avvenire se i due quark del mesone si fondono a formare un bosone W2. Il processo, però, potrebbe aver luogo anche per il tramite di un bosone di Higgs dotato di carica elettrica: se tale particella esistesse, la massa potrebbe essere ricavata sulla base delle deviazioni della probabilità di decadimento rispetto al caso in cui al processo partecipi il solo W. Ulteriori decadimenti utili nella ricerca di nuove particelle virtuali sono quelli in cui un leptone decade in uno di altro tipo senza emettere neutrini (LFV, Lepton flavour violation). Tali processi sono contemplati non dal Modello Standard, ma dalle estensioni che prevedono l’esistenza di repliche degli attuali leptoni. Gli odierni esperimenti con mesoni B, ossia BaBar e Belle, producono grandi quantità di leptoni t, i più facili da ottenere in abbondanza e in un ambiente pulito, e stanno cercando attivamente, anche se per il momento senza successo, tracce di LFV.
Prospettive future
Il Large hadron collider (LHC) del CERN si propone di raggiungere energie molto più elevate di quelle ottenute finora e dunque di cercare il bosone di Higgs, o altre particelle previste da nuovi modelli, esplorando intervalli di massa finora inaccessibili. Nel 2009 dovrebbe iniziare a produrre collisioni pp a 14 TeV nel centro di massa, mentre i due esperimenti ATLAS e CMS potrebbero registrare i primi segnali di nuove particelle nel 2010. Questi esperimenti saranno decisivi per determinare le prospettive a lungo termine: se, per esempio, gli esperimenti dell’LHC non dovessero osservare alcuna nuova particella elementare, occorrerebbe rivedere il modello e cercare particelle o forme di interazione nuove a energie estremamente più elevate. Ciò sarebbe possibile esclusivamente sfruttando le particelle di altissima energia provenienti dal cosmo e prodotte al di fuori dell’atmosfera. Se invece si cominciassero a osservare nuove particelle elementari, come il modello prevede, la sfida successiva sarà comprendere in che modo gli stati osservati debbano essere abbinati alle particelle previste. A tal fine occorrerà progettare esperimenti ad hoc per studiare le proprietà di interazione e decadimento di questi nuovi corpuscoli, in quanto gli acceleratori adronici come l’LHC non forniscono un ambiente sufficientemente pulito: a questo scopo si sta progettando l’ILC.
Anche per la fisica dei neutrini si prevede un grande sviluppo nel prossimo decennio. Da un lato, il fatto che i neutrini abbiano massa e che avvenga il mescolamento tra le loro tre famiglie sono scoperte molto recenti che vanno confermate. Dall’altro, alcuni parametri del modello sono ancora completamente ignoti: si tratta dell’angolo di mescolamento, del grado di violazione della simmetria CP nei decadimenti dei neutrini e infine della scala assoluta della loro massa. Le misurazioni degli angoli di mescolamento avvengono tipicamente in esperimenti con neutrini generati da fasci di particelle o da reattori nucleari, e gli apparati di prossima generazione, come Opera, Minos, T2K e Kamland, sono già nella fase della raccolta dei dati, o comunque in costruzione. La misurazione assoluta della massa dei neutrini è invece affidata allo studio dei decadimenti di un nucleo con emissione di due elettroni, come per esempio nell’esperimento Cuore che sarà condotto presso i Laboratori Nazionali del Gran Sasso. Le prospettive a lungo termine per la fisica dei neutrini sono legate alla possibilità di creare fasci molto intensi, quali si possono ottenere dal decadimento radioattivo di nuclei accelerati o di muoni accumulati in un anello.
Per quel che riguarda la fisica dei mesoni K e B, si stanno ancora discutendo le finalità e le modalità della prossima generazione di esperimenti. A parte la necessità di raffinare le misure attuali, si è già evidenziato come lo studio di processi rari a bassa energia possa fornire informazioni su nuove particelle di masse molto superiori. In particolare, la ricerca del decadimento K →πνν̅ o esperimenti con mesoni B ad altissima luminosità (le cosiddette super-B factories) potrebbero aiutare a comprendere la natura delle particelle eventualmente scoperte all’LHC molto prima che ciò sia permesso dall’ILC.