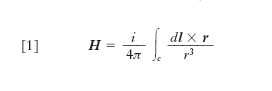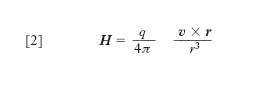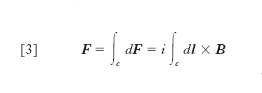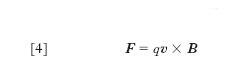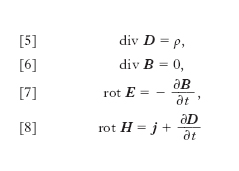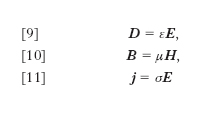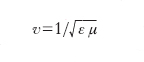elettromagnetismo

Settore della fisica avente per oggetto lo studio dei legami tra fenomeni elettrici e fenomeni magnetici. Tali legami sono fondamentalmente: a) una corrente elettrica genera un campo magnetico; b) un campo magnetico esercita una forza ponderomotrice su un conduttore percorso da corrente in esso immerso; c) un campo magnetico variabile o in moto relativo rispetto a un conduttore in esso immerso induce nel conduttore una forza elettromotrice.

E. premaxwelliano

Alla base dell’e. vi è la scoperta, compiuta da H.C. Oersted (1820), che in presenza di un conduttore percorso da corrente un ago magnetico devia dalla sua posizione ordinaria di equilibrio. A.-M. Ampère estese i risultati del fisico danese e pose i fondamenti logici e matematici della nuova scienza. Seguirono, nello stesso anno e nel successivo, le ricerche di J.-B. Biot e F. Savart e di P.-S. Laplace intorno alla valutazione quantitativa della forza esercitata da un circuito percorso da corrente su un ago magnetico. Sempre nel 1820, J.-F.-D. Arago e T.J. Seebeck magnetizzarono l’acciaio facendogli circolare attorno una corrente elettrica e crearono così il primo elettromagnete. Frattanto Ampère, proseguendo le sue ricerche sui legami tra correnti e magneti, era portato a concludere che fenomeni elettrici e magnetici sono tra loro intimamente connessi; che le proprietà dei corpi magnetizzati si possono attribuire a correnti permanenti circolanti negli atomi e nelle molecole; che tra due circuiti percorsi da corrente si destano azioni meccaniche (dette poi elettrodinamiche) analoghe a quelle esercitantisi tra una corrente e un magnete. Parallelamente, a opera di M. Faraday, venivano messi in luce i fenomeni dell’induzione elettromagnetica e dell’autoinduzione. I fondamenti dell’ e. classico possono essere riassunti in tre punti fondamentali.

Prima legge di Laplace

- Un circuito c percorso da una corrente stazionaria (o quasi stazionaria) di intensità i genera nello spazio circostante un campo magnetico la cui intensità H nel generico punto P vale

in unità del sistema internazionale (SI), dove dl è l’elemento generico di circuito, orientato nel verso della corrente e r la distanza orientata da dl a P. Questa legge non è verificabile in termini infinitesimi per l’impossibilità di isolare un elemento di circuito dl, o, se si vuole, un ‘elemento di corrente’ idl e intanto ha significato fisico in quanto dà conto del risultato globale, cioè dell’intensità del campo in P, grandezza, quest’ultima, suscettibile di misurazione diretta. Nel caso poi che a costituire la corrente sia una carica libera, q, in moto con velocità v costante e piccola rispetto a quella della luce nel vuoto, si ha

,

essendo, istante per istante, r la distanza orientata che va dalla posizione occupata dalla particella al punto P; se v non è molto piccola rispetto alla velocità della luce, occorre apportare opportune correzioni relativistiche. Se le particelle in moto sono più d’una, H è il risultante dei campi generati da ciascuna particella: la relazione [1] è un caso particolare della [2] applicata a un sistema di cariche in moto.

Seconda legge di Laplace

- Un circuito c percorso da una corrente di intensità i subisce da parte di un campo magnetico una forza:

,

dove dl è l’elemento generico di circuito, orientato nel verso della corrente e B l’induzione del campo. Nel caso infine che a costituire la corrente sia una sola particella di carica q, in moto con velocità v, il campo esercita su essa la forza (forza di Lorentz):

Come si verifica, la relazione [3] risulta dall’applicazione della [4] a un sistema di cariche in moto nel campo magnetico. La forza di Lorentz, risultando ortogonale alla velocità, non compie lavoro e non altera l’energia della particella.

Principio di equivalenza di Ampère

- Un circuito percorso da corrente è del tutto equivalente a un ago magnetico caratterizzato da un opportuno momento magnetico m, la cui intensità, direzione e verso dipendono dall’intensità i e dal verso della corrente nel circuito, nonché dalla configurazione di quest’ultimo. Nel caso, particolarmente semplice, che il circuito sia a forma di spira circolare piana, il momento dell’ago magnetico a esso equivalente si intende applicato nel centro della spira e vale m=µi Sn, essendo S l’area della spira, n il versore della normale alla spira, orientato (regola di Ampère) in modo che esso, personificato, veda la corrente scorrere nel circuito nel verso antiorario. Per l’equivalenza anzidetta, l’azione che il circuito risente da parte di un campo magnetico è la stessa che risentirebbe un magnete a esso equivalente, cioè di identico momento m; inoltre il campo magnetico generato dal circuito in punti abbastanza lontani da esso ha, come si deduce applicando la prima legge di Laplace, la stessa intensità di quello generato da un magnete a esso equivalente. È bene osservare peraltro che l’equivalenza tra campi magnetici generati da circuiti e campi generati da magneti non si estende alle proprietà dei campi stessi: infatti il campo generato da un magnete è conservativo, mentre quello generato da un circuito non lo è.

L’e. maxwelliano e postmaxwelliano

Le ricerche intorno all’e., tra la scoperta di Oersted del 1820 e la pubblicazione delle Experimental researches di M. Faraday ultimata nel 1855, costituiscono, specialmente gli ultimi lavori di Faraday, il presupposto fondamentale da cui si sviluppa l’opera di J.C. Maxwell (➔ elettricità), dominata peraltro da nuove geniali concezioni e principalmente dall’idea, tanto ardita quanto feconda, della corrente di spostamento (o di induzione) nei dielettrici. La teoria di Maxwell (1873) è una mirabile sintesi, tuttora valida nei suoi aspetti essenziali, non solo delle leggi e dei fenomeni dell’e., ma anche dell’elettrostatica e della magnetostatica. Essa si compendia nelle celebri equazioni di Maxwell: siano, in un generico punto di un certo mezzo e a un istante t generico, E e H rispettivamente il campo elettrico e il campo magnetico, D e B le corrispondenti induzioni elettrica e magnetica, ρ la densità di carica elettrica, j la densità della corrente elettrica di conduzione; istante per istante e punto per punto queste grandezze soddisfano a equazioni che, nel sistema internazionale di unità di misura (SI), si presentano nella forma:

Ognuna di queste equazioni ha un immediato e importante significato fisico. La [5] rappresenta il teorema di Gauss per il campo elettrico in termini differenziali: essa esprime il fatto che le sorgenti (positive o negative) del campo elettrico sono le cariche elettriche isolate (positive o negative). La [6] dà conto della inesistenza di sorgenti isolate (positive o negative) del campo magnetico, cioè che a ogni polo magnetico è sempre associato un polo di uguale valore e segno opposto. La [7] è la formula di Faraday-Neumann-Lenz dell’induzione elettromagnetica in termini vettoriali, e la [8] è il teorema della circuitazione del campo magnetico; le due, insieme, esprimono il fatto che un campo magnetico variabile dà luogo a un campo elettrico variabile, e viceversa, i due campi costituendo un tutt’uno inscindibile, il campo elettromagnetico. Alle quattro precedenti equazioni se ne aggiungono altre tre (equazioni costitutive); precisamente se ε, μ, σ sono la costante dielettrica assoluta, la permeabilità magnetica assoluta, la conduttività del mezzo, rispettivamente, si ha:

La [11] esprime la legge di Ohm. In generale, ε, μ, σ variano al variare del punto che si considera e del tempo; in particolare, poi, può anche risultare che ε sia funzione di E (mezzi ferroelettrici), che μ sia funzione di H (mezzi ferromagnetici), che σ sia funzione di E (mezzi conduttori non lineari).

Una delle caratteristiche essenziali dell’elettrologia maxwelliana rispetto alla precedente è che da essa resta eliminata ogni azione a distanza: ciò è analiticamente ben visibile dalle equazioni, in cui non intervengono a determinare il campo elettromagnetico altro che proprietà locali del campo medesimo (individuate da ∂D/∂t e ∂B/∂t). La teoria di Maxwell è stata sorgente di sviluppi estremamente importanti in vari campi: basterà qui ricordare una conseguenza che Maxwell medesimo trasse dalle equazioni, il fatto cioè che un campo elettromagnetico si propaga in forma di onde (➔ campo, onda), con velocità di propagazione

Nel vuoto questa formula dà per v il valore della velocità della luce: fu proprio da tale circostanza che Maxwell fu indotto a postulare la natura elettromagnetica della luce.

Le intuizioni di Maxwell aprirono la via alle esperienze di H.R. Hertz sulle onde elettromagnetiche generate da oscillatori elettrici ed ebbero da esse, meno di 20 anni dopo (1887), la più esauriente conferma sperimentale. La ragion d’essere e il significato più profondo dei fenomeni elettromagnetici hanno potuto peraltro essere in gran parte chiariti solamente attraverso la teoria della relatività. La fisica quantistica ha poi dato vita a una nuova teoria dell’e., l’elettrodinamica quantistica, per la descrizione dei fenomeni microscopici (➔ elettrodinamica).