induzione

Procedimento logico, mediante il quale si passa dalla considerazione di casi particolari a una conclusione universale.

Nel linguaggio scientifico, in genere, modificazione che determinate proprietà di un corpo subiscono per la vicinanza di un altro corpo.

Filosofia

Problema a lungo dibattuto è stato quello dei limiti e della giustificazione del processo induttivo. In Aristotele l’i. è contrapposta alla deduzione sillogistica e può raggiungere solo dei risultati parziali, non potendo scoprire l’essenza del genere esaminato: con essa ci si limita alla semplice indicazione di caratteri comuni rintracciabili nell’insieme di individui effettivamente osservati. Malgrado l’i. sia sempre imperfetta e non raggiunga la necessità propria della scienza, pur tuttavia può essere utilizzata nella retorica a fini persuasivi. La medesima svalutazione dell’i. è presente in tutta la filosofia antica e medievale, con la sola eccezione degli epicurei.

Nella filosofia moderna e contemporanea si assiste a un sempre più deciso rifiuto dell’i. come processo in grado di raggiungere conclusioni universali, ma questo rifiuto non sempre è accompagnato da una definitiva liquidazione dell’i. e dall’affermazione che essa ha un valore secondario rispetto alla via privilegiata della scienza. Nel 17° sec., infatti, se R. Descartes e i cartesiani riaffermavano la svalutazione sostanzialmente aristotelica dell’i., F. Bacone si impegnava a riqualificarla, per farne la base principale della scienza. Non si tratta più di fondare la conclusione universale su un’enumerazione completa dei particolari, quanto piuttosto di giungervi attraverso la convalida di un’ipotesi fondata sull’esperienza di un numero limitato di casi. Ma Bacone legava ancora l’i. all’universale. Nel 18° sec. la critica di D. Hume mise in crisi proprio questo legame, avviando l’analisi dell’i. nella direzione dello studio di una tecnica in grado di raggiungere conclusioni solo generali e probabili. Dopo Hume, malgrado il tentativo di I. Kant di fondare sulle condizioni trascendentali della conoscenza la capacità universalizzante dell’i., andò sempre più affermandosi nel 19° e nel 20° sec. la tendenza a concepire l’i. come una tecnica in grado di raggiungere solo conclusioni generali, valide per gli individui di una certa classe che non sono stati ancora osservati, con un grado maggiore o minore di probabilità e comunque mai con assoluta necessità. Il tentativo di J.S. Mill di riaffermare la validità oggettiva delle conclusioni dell’i. facendole dipendere da leggi causali rappresenta piuttosto un’eccezione. Per il resto, predomina lo sforzo di determinare i vari gradi di probabilità che una conclusione induttiva raggiunge a seconda dell’estensione dell’universo di individui osservati.

L’i. come processo probabilistico è stata spesso ritenuta nel 20° sec. la regola metodologica centrale della ricerca scientifica. Tuttavia, pur senza negare la legittimità dell’i., nella filosofia della scienza contemporanea non è mancato chi (come C.G. Hempel) ne ha messo in evidenza le insormontabili difficoltà logiche o chi, in contrasto con gli obiettivi neopositivistici di fondazione logico-probabilistica e in un rinnovato spirito humeano (come N. Goodman), ne ha segnalato il carattere di procedura eminentemente pragmatico-linguistica non ulteriormente riconducibile a qualche forma di inferenza logico-sintattica. Più radicale il punto di vista di K. Popper, che ha invece negato la legittimità stessa dell’i. e la possibilità di pervenire alla formulazione di leggi e teorie scientifiche attraverso l’accumulo dei casi di conferma di ipotesi date, ravvisando per contro nel metodo per prova ed errore, nel controllo empirico di asserti singolari dedotti da ipotesi escogitate in modo non induttivo, il carattere fondamentalmente deduttivo della ricerca scientifica.

Biologia

Embriologia

Il processo dell’i. embrionale si verifica quando una cellula o un gruppo di cellule differenziate governano lo sviluppo delle cellule vicine. La strategia seguita per dare origine a cellule organizzate in un individuo pluricellulare è ancora poco conosciuta se non nelle sue linee più generali: l’organizzazione comincia dalle semplici asimmetrie chimiche dell’uovo, nel quale componenti diverse sono concentrate in regioni specifiche del citoplasma o della membrana e viene completata e dettagliata dalle interazioni fra cellule. La diversificazione delle cellule che ne consegue dipende poi da informazioni posizionali fra le cellule e da programmi intercellulari che cambiano nel tempo in funzione dei segnali ricevuti. Per assumere infatti caratteristiche morfologiche e funzionali peculiari, ogni cellula del corpo in via di sviluppo deve, innanzi tutto, conoscere la sua posizione rispetto alle altre. Affinché un campo di sviluppo maturi in un organo o in un tessuto funzionale, tutte le cellule, nel giusto numero e nelle giuste proporzioni, devono essere indotte verso un loro specifico destino.

Le molteplici prove sperimentali accumulate in modelli di sviluppo animali ha consentito di stabilire la natura chimica di varie sostanze che possono fungere da induttori. Molto studiato è stato il differenziamento della vulva del nematode Caenorhabditis elegans, che costituisce un buon modello per identificare le molecole coinvolte nell’i. e capire l’organizzazione delle vie di trasmissione del segnale, che appaiono conservate nel corso dell’evoluzione nella maggior parte del regno animale. La vulva, deputata alla deposizione delle uova, è un’apertura ventrale nella pelle (ipoderma) del corpo del nematode. Varie cellule dell’ipoderma sono dotate della capacità potenziale di costruire le varie parti della vulva e costituiscono inizialmente un gruppo di equivalenza o campo di sviluppo. Esperimenti di microchirurgia hanno dimostrato che il determinante fondamentale dal quale dipende l’assegnazione dei diversi ruoli è un’unica cellula, detta ancora. Il gene lin-3 della cellula ancora codifica una proteina simile al fattore di crescita dell’epidermide (EGF) che si lega a un recettore tirosinchinasico presente in tutte le altre cellule. Solo la cellula che riceve il livello più alto di questo segnale, quella più vicina alla cellula ancora, attiva i fattori di trascrizione necessari per diventare la cellula primaria della vulva. Stabilito il suo destino, la cellula impedisce alle due cellule più vicine di interpretare i segnali inviati dalla cellula ancora. Questo processo di inibizione porta le due cellule vicine a seguire un diverso destino, quello di cellule secondarie. Le rimanenti cellule del gruppo di equivalenza, dette terziarie, contribuiscono alla formazione dell’ipoderma che circonda la vulva. Per ognuno dei tre tipi cellulari appartenenti allo stesso campo di sviluppo viene quindi attivato un gruppo di fattori di trascrizione specifici dello stato primario, secondario o terziario della cellula; si è osservato che i geni coinvolti codificano proteine molto simili a quelle che fanno parte di vie di trasmissione di segnali anche nei Vertebrati.

Genetica

In genetica molecolare, il processo di i. consiste nell’eliminazione della repressione di un gene o di un gruppo di geni che soggiace a un controllo negativo. La produzione di un determinato enzima da parte di una cellula avviene infatti in presenza di una sostanza specifica (detta induttore): per es., il batterio Escherichia coli utilizza come fonte di energia il glucosio, ma cresce anche in colture in cui il glucosio sia sostituito dal lattosio; in tali colture, infatti, la presenza di lattosio stimola la produzione dell’enzima β-galattosidasi (che normalmente non viene prodotto dalla cellula batterica), che scinde il lattosio in glucosio e galattosio. Le proteine, la cui sintesi è attivata dagli induttori sono dette inducibili (➔ regolazione). Dopo questi classici esperimenti, molti ricercatori hanno tentato di scoprire altri fenomeni di i. della trascrizione genica. Sebbene i loro sforzi abbiano avuto un considerevole successo, l’i. di geni da parte di fattori ambientali e nutritivi sembra essere un fenomeno diffuso più fra i Procarioti che fra gli Eucarioti. Gli esempi più studiati di espressione genica inducibile negli Eucarioti sono l’i. da parte di fattori ambientali (temperatura, luce) e l’i. dovuta alle molecole segnale quali, per es., gli ormoni e i fattori di crescita.

I. della trascrizione dovuta alla temperatura

Quando gli organismi vengono sottoposti ad alte temperature, rispondono sintetizzando un gruppo di proteine che aiuta a stabilizzare l’ambiente cellulare interno delle HSP (heat-shock protein), presenti sia negli Eucarioti sia nei Procarioti. In Drosophila melanogaster è stato ben studiato il processo di i. della trascrizione di Hsp70, una proteina di peso molecolare 70.000: quando la temperatura supera i 33 °C, un fattore di trascrizione chiamato HSTF (heat-shock transcription factor) viene fosforilato e si lega alle sequenze nucleotidiche a monte dei geni Hsp70 (dette HRE, heat-shock response elements), facilitando la loro trascrizione da parte della RNA-polimerasi.

I. della trascrizione dovuta alla luce

La proteina più abbondante sulla Terra è la ribulosio 1,5-bifosfato carbossilasi (RBC), un enzima che svolge un ruolo essenziale nella fotosintesi delle piante verdi. L’esposizione alla luce induce la produzione di questo enzima chiave della fotosintesi con un processo non ancora ben conosciuto. L’enzima è costituito da una subunità grande e una piccola. I geni che codificano le due subunità, in alcune piante, sono localizzati nel DNA del cloroplasto, mentre in altre piante i geni della subunità piccola sono localizzati nel DNA nucleare e quelli della subunità grande nel DNA del cloroplasto. I processi che determinano l’espressione del gene nucleare rbcS (ribulose biphosphate carboxylase Small), indotta dalla luce, sono solo in parte compresi: un evento importante è sicuramente l’assorbimento della luce da parte di una proteina citoplasmatica chiamata fitocromo, alla quale è legata una molecola che assorbe la luce (cromoforo). L’assorbimento della luce da parte del cromoforo causa un cambiamento conformazionale nel fitocromo che determina cambiamenti analoghi in altre proteine, le quali, presumibilmente, inducono la trascrizione di rbcS. Un processo simile sembra impiegato anche per la trascrizione della subunità grande di RBC.

I. della trascrizione per opera di molecole segnale

L’attività trascrizionale può essere indotta da ormoni peptidici, da vari tipi di proteine circolanti secrete, quali il fattore di crescita nervoso e il fattore di crescita dell’epidermide, e da molecole non circolanti associate alla superficie cellulare o alla matrice extracellulare. Sebbene ogni molecola abbia caratteristiche proprie, l’i. avviene secondo un processo comune durante il quale l’interazione fra la proteina segnale e un recettore legato alla membrana cellulare dà inizio a una catena di eventi all’interno della cellula che, alla fine, determina il legame di specifici fattori di trascrizione ai particolari geni che devono essere trascritti.

Chimica

Periodo di i.

In alcune reazioni chimiche si chiama così un intervallo di tempo iniziale durante il quale il processo appare quiescente. Un esempio viene offerto dalla reazione di riduzione degli ioni IO₃⁻ a iodio con acido solforoso secondo lo schema:

5SO₃⁻⁻+2IO₃⁻+2H⁺ → 5SO₄⁻⁻+I₂+H₂O. Se alla soluzione si aggiunge della salda d’amido, all’inizio resta incolore, come se non fosse presente iodio libero, e soltanto dopo un certo intervallo di tempo compare la colorazione blu, caratteristica della formazione del complesso tra lo iodio e l’amido. Il fenomeno si spiega ammettendo che la reazione si produca in tre fasi: lenta (a), veloce (b), molto veloce (c):

a) IO₃⁻+3SO₃⁻ → I^–+3SO₄⁻⁻

b) IO₃⁻+5I⁻+6H⁺ → 3I₂+3H₂O

c) I₂+SO₃⁻+H₂O → 2I⁻+SO₄⁻⁻+2H⁺.

All’inizio gli ioni iodio prodotti nella reazione a), vengono ossidati a iodio secondo la reazione b) e quindi ridotti di nuovo a ioni iodio secondo la reazione c). Quando la concentrazione degli ioni SO₃⁻⁻ è molto diminuita, la velocità della reazione c) diventa molto piccola e allora la concentrazione dello iodio libero aumenta e compare la colorazione blu.

In altri casi il periodo di i. è legato a fenomeni autocatalitici: così la reazione di ossidazione dell’acido ossalico con il permanganato in soluzione acida, lenta all’inizio, dopo qualche tempo diviene molto veloce perché catalizzata dagli ioni manganosi che si vanno via via formando.

Fisica

I. elettrica

fig. 1A

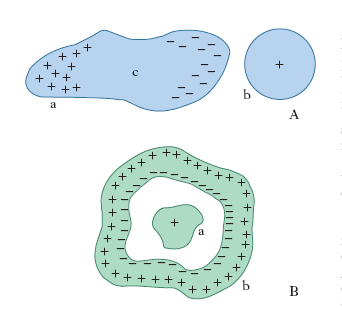
Fenomeno che si verifica quando un conduttore a (corpo indotto) viene esposto al campo elettrico generato da un corpo carico b (induttore), esso si elettrizza a sua volta: sulla sua superficie si manifestano infatti cariche elettriche (cariche indotte), di segno opposto alla carica di b nella parte vicina a b medesimo, di ugual segno nella parte lontana (fig. 1A). Allontanando sufficientemente a e b, le cariche indotte spariscono e l’indotto torna al suo stato di neutralità elettrica; se invece, tenendo a accostato a b, si asportano da a le cariche di un segno, per es., toccando con un dito l’estremità lontana, l’indotto resta carico anche quando sia estratto dal campo: è questo uno dei procedimenti per caricare un conduttore (elettrizzazione per i.). La spiegazione del fenomeno sta nel fatto che gli elettroni di conduzione, liberi di muoversi in a, vengono sollecitati dal campo elettrico ad addensarsi da una parte e a rarefarsi dall’altra, con il conseguente manifestarsi di una carica negativa da un lato e positiva dall’altro; tale separazione di carica non prosegue indefinitamente: in un tempo molto breve si raggiunge una situazione di equilibrio in cui nel corpo indotto l’azione del campo primario prodotto dal corpo induttore viene compensata esattamente da quella del campo secondario derivante dalle cariche separate sulla superficie dell’indotto, per modo che, come vogliono le leggi dell’elettrostatica, il campo nell’interno di quest’ultimo sia nullo e la superficie di esso sia equipotenziale. Com’è intuitivo, vi è tutta una zona della superficie dell’indotto, detta zona neutra (c in fig. 1A), in cui non si manifestano cariche indotte; l’estensione e la posizione di questa zona dipendono, in maniera non semplice, dalla forma e dalla posizione reciproca dei due corpi. Il campo elettrico generato dal corpo inducente risulta ‘deformato’ dalla presenza del corpo indotto: precisamente, in tutto lo spazio occupato dall’indotto, il campo, come abbiamo detto, diventa nullo e le linee di forza si modificano in modo da incidere perpendicolarmente sulla superficie dell’indotto.

Un caso assai importante è quello della cosiddetta i. completa, che si realizza quando le linee di forza uscenti dall’intera superficie dell’induttore terminano tutte sulla superficie dell’indotto. Ciò accade senz’altro se uno dei corpi circonda completamente l’altro, come nel caso della fig. 1B: se si comunica, in un modo qualunque, una carica Q al corpo induttore a, sulla superficie dell’indotto b affacciata ad a si desta una carica che complessivamente vale −Q, vale a dire che la carica indotta è, a parte il segno, uguale a quella inducente. La condizione che una delle due superfici conduttrici circondi completamente l’altra non è peraltro indispensabile perché si abbia i. completa: per es., se l’induttore e l’indotto sono due lamine parallele, piane o no, separate da una distanza piccola rispetto alla più piccola delle loro dimensioni l’i. tra loro può considerarsi completa se, com’è lecito fare, si trascura quel che accade ai bordi, dove, per l’inflettersi all’esterno delle linee di forza, alcune di queste potrebbero chiudersi su altri conduttori circostanti e non sull’altra superficie (fenomeno cosiddetto del flusso elettrico disperso). Sul fenomeno dell’i. completa sono basati i collettori di carica, gli schermi elettrici e, soprattutto, i condensatori elettrici.

Induzione elettromagnetica

fig. 2

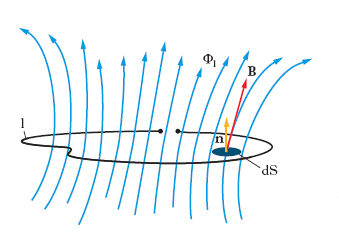
Fenomeno, scoperto da M. Faraday intorno al 1831, consistente nel fatto che se un circuito elettrico è posto in un campo magnetico, al variare del flusso d’i. magnetica concatenato con il circuito si manifesta in quest’ultimo una forza elettromotrice. Precisamente, si consideri un conduttore filiforme l disposto a spira (di forma qualunque, anche non piana), immerso in un campo magnetico di cui B sia il vettore induzione; se l è chiuso oppure se, essendo aperto, i suoi estremi sono abbastanza vicini tra loro, ha senso pensare l come contorno di una superficie S, peraltro arbitraria: dato che B è solenoidale, resta definito in modo univoco il flusso di i. magnetica concatenato con il circuito come il flusso di B attraverso S: Φ_l(B)=ʃ_sB∙ndS, dove n è il vettore, di modulo unitario, perpendicolare all’elemento di superficie dS considerato (fig. 2). Se Φ_l(B) varia con il tempo t, in l insorge una forza elettromotrice indotta, f=−dΦ_l(B)/dt (legge o formula di Faraday-Neumann-Lenz); il segno meno sta a significare che f è tale da opporsi alla variazione di flusso determinante il fenomeno (legge di E.C. Lenz). Se, in particolare, il conduttore l è chiuso, f determina in esso il passaggio di una corrente elettrica (corrente indotta) la cui intensità vale, ovviamente, i=[−dΦ_l(B)/dt]/R, essendo R la resistenza del circuito. La legge di Faraday-Neumann-Lenz, ove si ricordi che la forza elettromotrice è la circuitazione dell’intensità del campo elettromotore, E, e si tenga poi presente il teorema di Stokes della circuitazione, può essere scritta: rot E = −∂B/∂t; in tale forma tale legge costituisce una delle equazioni di Maxwell dell’elettromagnetismo.

L’autoinduzione elettromagnetica è un caso particolare di i. elettromagnetica consistente nel fatto che, se in un circuito varia l’intensità della corrente, nel circuito medesimo insorge una forza elettromotrice autoindotta, e quindi una corrente autoindotta (detta anche corrente parassita), tale da opporsi alla variazione di intensità che l’ha provocata. Ciò accade in quanto il circuito è immerso nel campo magnetico da esso stesso generato, la cui i. dipende dall’intensità i della corrente; se varia i, varia l’i. e, insieme, il flusso d’i. concatenato con il circuito; insorge allora una forza elettromotrice f. Come si riconosce, il flusso d’i. concatenato, o meglio autoconcatenato, Φ_a(B), è proporzionale a i: Φ_a(B)=Li, dove L, detto coefficiente di autoinduzione o induttanza, è una grandezza dipendente soltanto dalla forma del circuito e dalla natura del mezzo circostante; a norma della legge di Faraday-Neumann-Lenz, risulta poi f=−d(Li)/dt, o anche, se L può considerarsi indipendente dal tempo t, f=−Ldi/dt (perché quest’ultima relazione sia vera occorre che la permeabilità magnetica del mezzo non dipenda da i, il che accade senz’altro se, per es., il mezzo in questione non è ferromagnetico).

La mutua i. elettromagnetica è un caso notevole di i. elettromagnetica consistente nel fatto che, se si hanno due circuiti percorsi da corrente, variando l’intensità della corrente in uno insorge nell’altro una forza elettromotrice, e quindi una corrente, e viceversa. Com’è chiaro, ciò accade in quanto ognuno dei due circuiti è immerso nel campo magnetico generato dall’altro, di modo che è possibile considerare un flusso d’i. generato dal primo e concatenato con il secondo, Φ₂(B₁), e un flusso d’i. generato dal secondo e concatenato con il primo, Φ₁(B₂). Se si indicano con i₁ e i₂ le intensità della corrente che percorre il primo e il secondo circuito, rispettivamente, si trova che è Φ₁(B₂)=Mi₂, Φ₂(B₁)=Mi₁, essendo M, una grandezza, detta coefficiente di mutua i. (o induttanza mutua), dipendente soltanto dalla forma e dalla posizione reciproca dei due circuiti, nonché dalla permeabilità magnetica del mezzo circostante. I fenomeni di i. elettromagnetica hanno enorme importanza nel campo delle applicazioni pratiche; basterà ricordare che su di essi sono basate le macchine elettriche appunto dette a i. (alternatori, dinamo, motori elettrici, trasformatori statici).

I. magnetica

Fenomeno che si verifica quando un corpo (indotto) viene sottoposto all’azione del campo magnetico che esce da un corpo magnetizzato (induttore), si magnetizza a sua volta. La spiegazione del fenomeno sta nei processi di magnetizzazione, per precessione di Larmor e per orientamento, che avvengono nel corpo indotto sotto l’azione del campo generato dall’induttore (➔ magnetismo). La magnetizzazione indotta scompare all’allontanarsi dall’induttore se il corpo che subisce l’i. è dia- o paramagnetico; permane invece, si ha cioè una magnetizzazione permanente, se il corpo è ferromagnetico. Converrà anzi aggiungere che il fenomeno ha rilevanza pratica soltanto per i corpi ferromagnetici, dato che negli altri avviene con intensità normalmente trascurabile.

Il vettore i. magnetica

È la grandezza vettoriale che dà conto delle azioni che un campo magnetico esercita su circuiti percorsi da corrente o, più in generale, su cariche elettriche in moto; la relazione di definizione operativa per B è dunque la 2ª legge di Laplace dell’elettromagnetismo. La proprietà fondamentale di tale vettore è espressa dalla relazione divB=0: il campo di i. magnetica è dunque solenoidale, cioè non ha sorgenti discrete o, che è lo stesso, le sorgenti sono dipoli e non poli isolati. È legato all’intensità del campo magnetico H dalla relazione B=μH, essendo μ la permeabilità magnetica assoluta del mezzo in cui esiste il campo. Unità di misura di B è, nel sistema internazionale SI, il tesla (1 T=1Wb/m²).

I. nucleare

Polarizzazione magnetica di un materiale, per orientamento dei momenti magnetici intrinseci dei nuclei atomici; è rivelabile mediante il fenomeno della risonanza magnetica nucleare (➔ risonanza).

Matematica

Definizione per i.

Un insieme I (o una proprietà P) si dice definito per i. se la sua definizione soddisfa le seguenti condizioni: 1) elementi di un dato tipo, detti elementi-base, appartengono a I (o godono di P); 2) comunque si scelgano elementi che appartengono a I (o godono di P), anche i risultati ottenuti applicando a quegli elementi delle operazioni prefissate appartengono a I (o godono di P); 3) si esclude che enti diversi da quelli indicati appartengano a I (o godano di P). Per es., una tipica definizione per i. è quella nell’insieme N dei numeri naturali. L’elemento-base è lo zero, l’operazione è quella di «successore»; si dirà allora: 1) zero appartiene a N; 2) se n appartiene a N, anche il successore di n deve appartenere a N; 3) nient’altro appartiene a N. Dimostrazione per i. Data una successione infinita di proposizioni matematiche: A₁, A₂, ... , A_n, A_n+1 ..., se risultano verificate le due seguenti condizioni: 1) la prima proposizione, A₁, è vera; 2) supponendo vera una qualsiasi proposizione della successione, per es. A_n, se ne deduce con un ragionamento la verità della successiva, A_n+1, allora tutte le infinite proposizioni della successione sono vere. È questo il cosiddetto principio di i. completa. Molto spesso tale principio si incontra in forme diverse, come per es.: «se una proprietà A è vera per il numero 1, e se supponendola vera per un intero n qualsiasi, si deduce che essa è vera anche per il successivo (ossia n + 1), essa è vera per tutti i numeri interi». In questa forma il principio (noto anche con il nome principio di i. forte) non può appartenere a una teoria del primo ordine in cui non si può esprimere il concetto «per ogni proprietà», non essendo quantificabili le variabili predicative. In queste teorie quindi il principio avrà una formulazione molto più debole.

Il principio di i. fornisce la giustificazione anche per le cosiddette definizioni ricorsive di funzioni aritmetiche. In generale, esse stabiliscono il valore di una funzione per l’argomento zero (e per eventuali parametri); poi stabiliscono il valore della funzione per l’argomento n+1, in dipendenza (oltre che dai parametri) da n e dal valore della funzione per n, utilizzando, se del caso, anche altre funzioni già note.

L’i. forte permette di dimostrare, data una definizione ricorsiva, che esiste una e una sola funzione definita per ogni numero naturale, avente come valori dei numeri naturali e soddisfacente le condizioni della definizione stessa. Si badi però che in una teoria dei numeri del primo ordine, in cui, come si è detto, il principio di i. sia esprimibile solo in modo attenuato, la dimostrazione di cui sopra non è più possibile; si è quindi costretti ad assumere le definizioni ricorsive, o almeno alcune di esse, quali assiomi. Mentre il principio di i. completa è generalmente accettato dai matematici per i numeri interi (sia pure come un postulato dell’aritmetica come fece G. Peano, 1899), vi è ancora discussione sulla sua estensione ai numeri ordinali transfiniti. Il principio di i. transfinita per i numeri transfiniti di classe I e II si enuncia così: per dimostrare che un teorema T è vero per ogni numero ordinale di classe I e II, basta provare che: 1) esso è vero per il numero 0; 2) se è vero per a è vero per a+1; 3) se è vero per una successione infinita crescente di numeri è vero anche per il numero limite di questa successione (numero che non ha un precedente immediato, e che pertanto non può essere raggiunto ripetendo il ragionamento 2) un numero finito di volte).

Molto importante, specialmente nelle scienze sperimentali, è un’altra forma di i. detta i. empirica o i. incompleta. Essa consiste nell’enunciare una legge valida in generale, basandosi soltanto su una successione finita di osservazioni, e ha un valore e un senso solo quando si suppongono validi certi caratteri di regolarità nel fenomeno studiato.

Medicina

I. ossea

La capacità, posseduta da alcuni tessuti e da particolari sostanze da essi estratte, di promuovere la formazione di tessuto osseo da parte dei connettivi normalmente privi di potere osteoformativo.

Psicologia

I. psichica

Trasferimento di idee e convinzioni da una persona a un’altra tramite procedimenti psichico-suggestivi.

Si indica con il termine psicosi da i. (follia indotta, contagio psichico) quel disturbo mentale la cui causa specifica è l’influenza immediata di un malato mentale, i cui convincimenti deliranti vengono assunti e accettati dall’indotto (folie à deux) o dagli indotti (i. di massa) senza alcuna critica, sia per suggestibilità sia per imitazione.

Tecnica

Dispositivi, apparecchi, procedimenti in cui vengono sfruttati fenomeni d’i. (per es., forno a i., macchina elettrica a i., tempra a i.) sono detti a induzione.