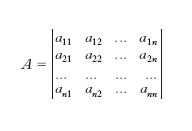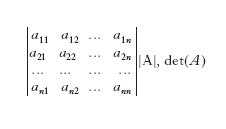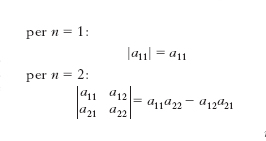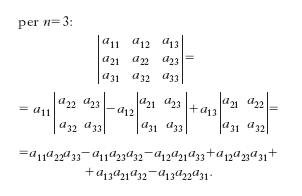determinante

Biologia

Termine introdotto da A. Weismann per indicare presunti aggregati di molecole contenuti nel nucleo delle cellule sessuali e che conterrebbero i fattori per la determinazione delle cellule.

In immunologia, d. antigenico, sito dell’antigene contro cui è diretta la specificità di un anticorpo; d. aptenico, macromolecola trasportatrice alla quale si lega una molecola di piccole dimensioni (aptene). Il legame tra l’aptene e il d. aptenico provoca la formazione di un complesso molecolare in grado di indurre una reazione anticorpale da parte dell’organismo.

Matematica

Si dice d. il valore che si associa, con ben determinata regola, a una matrice quadrata

e che si indica con una delle seguenti notazioni:

Il numero n è l’ordine del d.; la regola per il calcolo di un d. di ordine n è la seguente. Si considerino i prodotti a_1h1∙a_2h2∙...∙a_nhn, essendo h₁, h₂, ..., h_n i numeri 1, 2, ..., n in una delle loro possibili permutazioni (tali prodotti sono in numero di n!) e a ciascuno di tali prodotti si attribuisca il segno + o il segno – a seconda che la permutazione h₁, h₂, ..., h_n sia, rispetto alla permutazione 1, 2, ..., n, di classe pari o dispari: valore del d. è la somma algebrica dei prodotti considerati. Si ha, in particolare,

D. minore di ordine k del d. di ordine n di una matrice data A, è il d. di una sottomatrice quadrata di ordine k formata dagli elementi che si trovano all’incrocio di k righe e di k colonne di A. Per il calcolo effettivo di un d. di ordine qualunque si può utilizzare il primo teorema di Laplace: il d. di una matrice quadrata è uguale alla somma dei prodotti degli elementi di una prefissata riga (o colonna) per i rispettivi complementi algebrici, cioè per i minori quadrati estratti dalla matrice di partenza cancellando la riga e la colonna dell’elemento in esame e attribuendo a ciascun minore il segno + o − a seconda che sia pari o dispari la somma degli indici di riga e di colonna dell’elemento di cui è complemento. Si ha in particolare,

_.

Nel calcolo dei d. riescono inoltre utili talune regole e proprietà, tra le quali le seguenti. a) Se una matrice quadrata ha due linee (righe o colonne) uguali o proporzionali, ovvero se una linea è tutta nulla, ovvero se una linea è combinazione lineare di più linee parallele, il suo d. è nullo. b) Il valore del d. non si altera se a una linea si aggiunge una combinazione lineare qualunque di più linee parallele né se si scambiano di posto due linee parallele intervallate da un numero dispari di linee; cambia di segno se si scambiano di posto due linee parallele intervallate da un numero pari di linee. c) Se in una matrice gli elementi di una linea sono somme di n addendi, il suo d. è uguale alla somma degli n d. che si ottengono mettendo, al posto di quella linea, una volta la linea formata con i primi addendi, una volta la linea formata con i secondi, e così via, lasciando inalterate le altre linee.

La teoria dei d. permette di rendere assai compatti sviluppi analitici anche complessi: caso tipico è l’applicazione di questa teoria alla risoluzione dei sistemi di equazioni lineari. Di seguito sono riportate alcune proprietà dei d. che riguardano vari tipi di matrici e di operazioni tra di esse. Prodotto di matrici Siano A e B due matrici quadrate n×n a valori in un campo K, allora det(AB)=det(A)det(B) (teorema di Binet). Da questa proprietà discende immediatamente che, per ogni scalare c, det(cA)=cⁿdet(A); basta infatti scrivere cA=cI_nA, essendo I_n la matrice unità n-dimensionale, e ricordare che det(cI_n)= cⁿ. Matrice inversa Una matrice quadrata A a valori in un campo K è invertibile se e solo se det(A)≠0. In tal caso det(A⁻¹)=1/det(A). Matrice trasposta Il d. di una matrice A è uguale a quello della sua trasposta A^T: det(A)=det(A^T). Matrici hermitiane Il d. di una matrice complessa hermitiana, tale cioè che aik= āki, è reale.

Matrici emisimmetriche Il d. di una matrice emisimmetrica, tale cioè che a_ik=−a_ki, è nullo, se di ordine dispari, e uguale al quadrato di un polinomio, detto pfaffiano, costruito con i suoi elementi, se di ordine pari. Matrici triangolari In una matrice quadrata n×n gli elementi con due indici uguali (a_rr) costituiscono la diagonale principale, quelli per cui la somma degli indici è n+1 (ossia: a₁n, a₂,n₋₁, ..., an₁) la diagonale secondaria: se sono nulli tutti gli elementi al di sopra (o al di sotto) della diagonale principale, allora la matrice si dice triangolare e il suo d. è pari al prodotto degli elementi di tale diagonale; se sono nulli tutti gli elementi al di sopra (o al di sotto) della diagonale secondaria, il d. è pari al prodotto degli elementi di questa moltiplicato per (−1)^n(n−1)/2. Autovalori Siano λ_i, i=1,2,…,n, gli autovalori di una matrice A complessa di dimensione n×n, si ha allora det(A)= λ₁λ₂…λ_n. Da questa proprietà segue l’identità det(eA)=e^Tr(A), che permette di mettere in relazione il d. e la traccia di A.