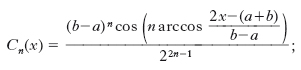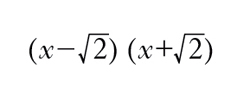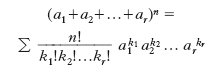polinomio

In matematica, somma di monomi (in senso proprio, solo con riferimento a monomi interi), detti termini del p.: binomio, trinomio, quadrinomio ecc., è un polinomio rispettivamente di 2, 3, 4 ecc. termini; coefficienti di un p. sono i coefficienti dei suoi monomi; grado di un p. rispetto a una lettera è il massimo grado, rispetto a quella lettera, dei monomi che lo compongono; il grado complessivo di un p. (o semplicemente il suo grado), rispetto a tutte le variabili, è il maggiore dei gradi dei suoi monomi, gradi valutati anch’essi rispetto al complesso delle variabili. Si ha un p. omogeneo quando tutti i termini hanno lo stesso grado; un p. ridotto quando siano stati sommati eventuali termini simili. Un p. di grado n in una variabile x si indica di solito con la scrittura

essendo a₀ il coefficiente direttore del polinomio. Un p. in r variabili di grado n si indica invece abitualmente con il simbolo

dove a_n1n2…_nr sono coefficienti e la somma va estesa a tutti i valori interi non negativi di n₁, n₂, …, n_r tali che n₁+n₂+…+n_r≤n; se il p. è ridotto, il numero complessivo dei suoi termini è espresso dal coefficiente binomiale (r + nn ) purché si tenga conto anche di eventuali termini nulli.

Anello dei p. in una indeterminata

I p. con coefficienti in un anello A e con un’unica variabile x (che si chiama, per lo più, indeterminata) hanno una struttura di anello che si indica con A [x] e si chiama anello dei p. in un’indeterminata su A. Molte proprietà dell’anello A (dette teoremi di trasporto) si ritrovano in A [x], come: a) il fatto che A [x] sia dotato di unità; b) che A [x] sia commutativo; c) che A [x] sia euclideo, ossia che in esso valga l’algoritmo euclideo delle divisioni successive (➔ Euclide); d) che A [x] sia principale ossia che ogni suo ideale sia costituito dai multipli di un opportuno elemento di A [x].

Anello dei p. in più indeterminate

I p. con coefficienti in un anello A e con 2, 3 o più indeterminate costituiscono ancora degli anelli che si indicano, a seconda dei casi, con A [x, y], A [x, y, z] ecc. Valgono ancora, come nel caso di una sola indeterminata, teoremi di trasporto. C’è tuttavia una differenza importante rispetto al caso di una sola variabile, e cioè che gli anelli A [x, y] ecc. non sono più principali. La nozione di ideale dei p. in più indeterminate ha grande importanza perché è alla base della definizione di varietà algebrica (➔ varietà).

P. di Čebyšev

Sono particolari p. di notevole importanza nella teoria dell’interpolazione. Precisamente, considerato un intervallo (a, b) dell’asse reale, si chiama p. di Čebyšev di ordine n relativo ad (a, b) e si indica con C_n(x) il p. monico (cioè un p. in una variabile il cui coefficiente direttore è uguale a 1), di ordine n, caratterizzato dal fatto di avere, tra tutti i p. monici del suo stesso ordine, il massimo del valore assoluto (relativamente all’intervallo a, b) più piccolo possibile. L’espressione analitica di C_n(x) è

che, nel caso che l’intervallo sia (−1, 1), si semplifica in cos(n arccosx)/2^2n–1; il massimo del modulo di C_n(x) è rispettivamente (b−a)ⁿ/2^2n–1 oppure 1/2ⁿ⁻¹. I p. di Čebyšev relativi all’intervallo (−1, 1) sono ortogonali rispetto al peso (1 − x²)^–1/2, e sono definiti per ricorrenza nel modo seguente: C₀(x)=1, C₁(x)=x, C_n+1=2xC_n(x)−C_n−1 (x), (n=1, 2 …). In ogni caso, C_n(x) ha n zeri reali tutti situati nell’intervallo base. L’importanza dei p. di Čebyšev è in relazione al problema di interpolare una data funzione f(x) mediante una successione di p. che converga uniformemente a f(x) nell’intervallo base considerato. Si tratta di sapere dove conviene scegliere i nodi dell’interpolazione, ossia i punti dell’asse x in relazione ai quali i p. interpolanti abbiano la medesima ordinata della funzione f(x). È stato stabilito da S.N. Bernštejn che se la funzione f(x) ha derivata prima limitata nell’intervallo base e se i nodi di interpolazione per il p. interpolante di ordine n si scelgono proprio nei nodi del p. di Čebyšev C_n, allora si è certi che la successione dei p. interpolanti converge uniformemente a f(x).

P. irriducibili

Un p. P(x) con coefficienti in un campo K si dice irriducibile su K se non può ottenersi come prodotto di due p. P₁(x) e P₂(x) anch’essi con coefficienti in K e di grado inferiore al grado di P(x). L’irriducibilità di un p. P(x) dipende in maniera essenziale dal campo K, e può accadere che un p. irriducibile in K divenga riducibile in un sopracampo K′ di K; così, x²−2 è irriducibile nel campo razionale ma è riducibile e uguale a

nel campo reale.

P. ortogonali

Un insieme di p. ortogonali è ogni insieme (finito o infinito) di p. che, relativamente a un certo intervallo (a, b) dell’asse reale, siano funzioni ortogonali, ossia tali che il prodotto di due qualunque di essi abbia integrale nullo su (a, b). Una proprietà generale dei p. ortogonali è che i loro zeri sono tutti reali, differenti l’uno dall’altro e contenuti nell’intervallo base (a, b). I p. ortogonali hanno applicazioni in varie questioni di analisi numerica: così talora, dovendosi approssimare una data funzione f(x) con uno sviluppo in serie, può essere preferibile utilizzare non una serie di Taylor ma una serie i cui termini siano appunto p. ortogonali di un particolare tipo, per es., i p. di Čebyšev.

P. trigonometrico

È ogni p. nelle funzioni seno e coseno: per es., cost+sen²t+cos³t. Un p. del genere si scrive abitualmente nella forma:

l’intero k si chiama grado del p. trigonometrico considerato.

Formula del polinomio

È la formula, detta anche formula di Leibniz, che generalizza la formula del binomio e dà lo sviluppo della potenza n-ma di un p.:

ove la sommatoria è estesa a tutti i valori dei numeri interi, non negativi, k₁…k_r, tali che k₁+k₂+…+k_r = n. I numeri n!/(k₁!k₂! … k_r!) si chiamano coefficienti o numeri polinomiali. Il numero dei termini dello sviluppo è, in generale, (r + n − 1n ). La formula del p. (come del resto quella del binomio) non vale se l’anello A nel quale si opera non è commutativo: in questo caso infatti non è possibile in generale eseguire la riduzione dei termini simili. Viceversa, se A, oltre a essere commutativo, ammette divisori dello zero, la formula può risultare ulteriormente semplificata.

Zeri di un polinomio

Sono le radici dell’equazione algebrica che si ottiene uguagliando a zero il p. stesso. Se il p. viene considerato nel corpo complesso C i suoi zeri sono tanti quant’è il grado del p. (teorema fondamentale dell’algebra), ma ciò non è più vero se a C si sostituisce un anello A. A questo proposito: a) se A è commutativo e privo di divisori dello zero, un p. di grado n a coefficienti in A ha al massimo n zeri in A, ma può non averne nessuno: si pensi, per es., a un qualsiasi p. a coefficienti reali; b) se A è commutativo ma ha divisori dello zero, un p. di grado n può avere più di n zeri ma può ancora viceversa non averne nessuno: per es., nell’anello Z₁₅ delle classi resto modulo 15, il p. x²−1 ha quattro zeri, e cioè 1, 4, 11, 14 (in effetti, 1²−1 = 0; 4²−1, 11²−1 e 14²−1 sono interi divisibili per 15 e perciò sono nulli in Z₁₅); viceversa, nell’anello Z₄ il polinomio x³+2x+2 non ha nessuno zero e infatti per i valori 0, 1, 2, 3 della variabile x assume rispettivamente i valori 2, 1, 2, 3; c) se A non è commutativo, un p. può avere addirittura infiniti zeri: per es., nel corpo H dei quaternioni il p. x²+1 ha come zeri tutti i quaternioni privi di parte reale e con modulo unitario.

Per il p. caratteristico di una matrice ➔ matrice; per il p. di Hermi;te ➔ Hermite, Charles; per i p. di Laguerre ➔ Laguerre, Edmond-Nicolas; per i p. di Legendre ➔ Legendre, Adrien-Marie.