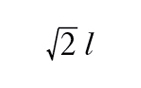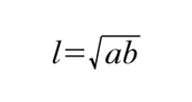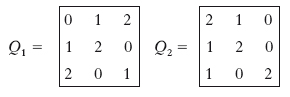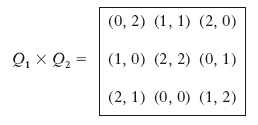quadrato

Matematica

fig. 1

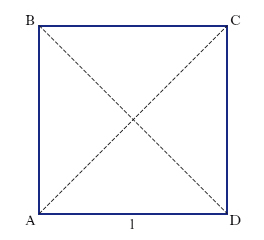
In geometria, figura piana costituita da un quadrilatero avente i 4 lati, e così pure i 4 angoli, fra loro uguali (fig. 1).Il q. è un parallelogramma (i lati opposti sono paralleli); è, insieme, un rettangolo (giacché è equiangolo) e un rombo (giacché è equilatero); le sue diagonali sono uguali e perpendicolari, e bisecano gli angoli interni: se l è la lunghezza del lato, l’area è data da l2 e la lunghezza della diagonale da

Il lato l del q. equivalente al rettangolo di lati a e b è medio proporzionale tra a e b, cioè

il q. circoscritto a un dato cerchio ha area doppia del q. inscritto nello stesso cerchio; il q. è uno dei 3 poligoni regolari (q., triangolo, esagono) con i quali è possibile ricoprire completamente il piano (pavimentazione a piastrelle regolari uguali).

Q. latino

Si chiama q. latino di ordine n una tabella quadrata di n righe ed n colonne nella quale ogni riga e ogni colonna è costituita dai numeri 0, 1, 2, …, n−1 disposti in un ordine qualsiasi, per es.:

I q. latini devono il nome al fatto che in un primo tempo si usava indicare con lettere latine gli elementi che li costituiscono; sono importanti perché forniscono la tabella moltiplicativa di un quasigruppo. A partire da due q. latini A, B dello stesso ordine n si può poi costruire il q. anch’esso di ordine n, che ha in ogni casella le coppie ordinate dei numeri che, in A e in B, occupano quella casella; tale nuovo q. si chiama q. greco-latino prodotto di A per B. Nel nostro caso:

Poiché Q₁×Q₂ è costituito da coppie tutte distinte si dice che Q₁ e Q₂ sono ortogonali. Non per ogni valore di n esistono però coppie di q. latini ortogonali; Eulero congetturò, nel 1782, che tali coppie non esistessero per n = 6, 10, 14, 18, …, ma la congettura è stata dimostrata esatta (Tarry, 1900) per il solo valore n = 6 e confutata (Parker, 1959) per gli altri valori.

Q. magici

Definizione

Si dà la denominazione di q. magico di ordine n a una tabella quadrata costituita dai primi n² numeri naturali disposti in maniera che la somma dei numeri contenuti in ciascuna riga, in ciascuna colonna e in ciascuna diagonale sia sempre la stessa (costante magica del q.). Poiché la somma 1+2+ … +n² è uguale a n²(n²+1)/2, la costante magica vale n(n²+1)/2. Non esiste nessun q. magico di ordine 2, mentre ne esiste uno solo di ordine 3 se si conviene di identificare un q. magico e tutti quelli che se ne ottengono per rotazione attorno al centro o per simmetria rispetto a una linea mediana. Esistono invece 880 q. magici di ordine 4 e circa 60.000 di ordine 5. Sono noti procedimenti per ottenere q. magici di ordine comunque elevato.

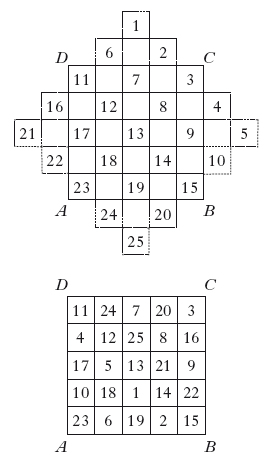
I q. magici sono noti fin dall’antichità: i matematici indiani conoscevano e sapevano costruire q. magici di ordine dispari. Ai q. magici si attribuivano spesso significati occulti e poteri misteriosi; la non esistenza di quelli di ordine 2 indicava, per es., l’imperfezione dei 4 elementi: terra, acqua, aria, fuoco. Lo studio dei q. magici costituisce un interessante capitolo della teoria dei numeri. 2.1 Costruzione di q. magici. Gli schemi seguenti illustrano uno dei metodi di costruzione valido per n dispari, nel caso n = 5 (metodo delle terrazze). Si passa dal primo schema al secondo facendo scorrere di 5 posti i numeri scritti nelle caselle aggiuntive (verso il basso, verso l’alto, verso destra e verso sinistra a seconda che si tratti delle caselle al di sopra di DC, al di sotto di AB, a sinistra di AD o a destra di BC):

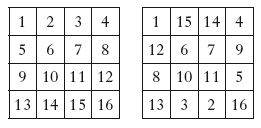
Gli schemi seguenti illustrano invece un procedimento, dovuto a P. de Fermat, per costruire q. magici di ordine 4; partendo dal q. di sinistra si lasciano fermi gli elementi sulle diagonali e si sostituisce a ciascuno degli altri il suo simmetrico rispetto al centro del q.:

Indichiamo infine un metodo, ideato da A. Makowski, per costruire q. magici di ordine m∙n partendo da un q. magico di ordine m e da uno di ordine n: si ottiene un q. magico di ordine m∙n sostituendo a ogni elemento h del primo q. il q. ottenuto dal secondo addizionando n²(h‒1) a ciascuno dei suoi elementi.

Utilizzando contemporaneamente i vari metodi esposti si possono costruire, oltre a q. magici di un ordine dispari qualsiasi, anche q. di ordine 12 (= 3∙4), 16 (= 4∙4), 20 (= 4∙5), 24 (= 3∙8) ecc.

Astronomia

Q. di Pegaso

Designazione popolare dell’aspetto caratteristico della costellazione di Pegaso, le cui stelle principali costituiscono in cielo i vertici di un grande quadrato.

Telecomunicazioni

fig. 2

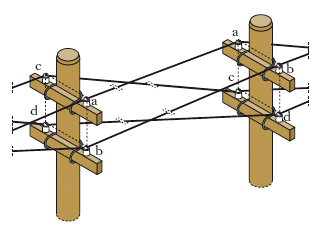
Nella tecnica delle linee telefoniche in fili aerei, insieme di 4 fili a, b, c, d (fig. 2) tesi sulla palificazione in modo che risultino disposti ai 4 vertici di un q.; con i 4 fili si costituiscono 2 circuiti bifilari, prendendo per ciascun circuito i fili disposti su una diagonale (circuiti bifilari a, d e b, c). La disposizione in q. consente di ridurre al minimo l’accoppiamento sia induttivo sia capacitivo tra i circuiti stessi e inoltre di realizzare, sui due circuiti che lo costituiscono, un circuito virtuale nelle migliori condizioni di disaccoppiamento verso gli altri circuiti. Al fine di ottenere che anche gli accoppiamenti con la terra e con altri circuiti esistenti sulla stessa palificazione siano minimi, la posizione nel q. dei 4 fili viene variata spostando di un posto sempre in uno stesso senso di rotazione la posizione dei fili sugli isolatori.