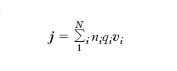corrènte

Astronomia

Correnti stellari

Locuzione, oggi in disuso, introdotta agli inizi del Novecento da J.C. Kapteyn per descrivere il moto d’assieme di gruppi di stelle. Nel 1927 J.H. Oort interpretò questi moti come un effetto della rotazione differenziale della galassia.

Fisica

Corrente elettrica

Corrente elettrica di conduzione

Con tale denominazione (spesso semplicemente c. elettrica) si intende un ordinato movimento d’insieme di cariche elettriche e anche l’insieme delle cariche in movimento. A prescindere dalla natura delle cariche e dalla natura del mezzo, perché in quest’ultimo scorra una c. occorre che le cariche siano sollecitate da un campo elettrico, cioè che i punti del mezzo siano a potenziale elettrico diverso. Il caso più semplice è quello in cui il mezzo considerato sia sostanzialmente vuoto: in questo caso la probabilità di interazione delle cariche elettriche con le particelle del mezzo è molto bassa e il moto delle cariche risulta uniformemente accelerato in presenza di campi elettrici costanti e uniformi, mentre esso è uniforme quando il campo elettrico è nullo. Molto più complesso è il caso in cui la c. elettrica abbia luogo in mezzi materiali, quali i conduttori. In tal caso le interazioni delle cariche elettriche con le particelle del mezzo sono molto frequenti e dipendono sia dalla natura del mezzo considerato sia dalla temperatura: in presenza di campo elettrico uniforme, le singole cariche elettriche subiscono successive azioni frenanti da parte del mezzo, con associata trasformazione di energia elettrica in calore (effetto Joule) per cui il moto d’insieme risulta sostanzialmente uniforme. Dal punto di vista macroscopico, si ottiene pertanto che le linee di c., cioè le linee del campo delle velocità di scorrimento delle cariche elettriche, coincidono con le linee di forza del campo elettrico. Quanto al verso positivo di percorrenza di esse, si è convenuto di assumere quello stesso delle linee del campo elettrico, il che equivale a dire che la c. scorre da punti a potenziale più alto verso punti a potenziale più basso.

Si chiama densità di c. il vettore j, orientato come il campo elettrico, il cui modulo è pari al rapporto tra la quantità di elettricità che attraversa nell’unità di tempo un elemento di superficie s ortogonale alla velocità di scorrimento e l’area di s. Se le cariche sono tutte della stessa specie è, evidentemente, j = nqv, essendo n il numero di cariche per unità di volume, q il valore di ogni carica, v la velocità di scorrimento. La definizione può essere generalizzata nel senso che se la c. fosse costituita dal moto di N specie di cariche, ciascuna caratterizzata da una densità ni, da un valore qi e da una velocità di scorrimento vi, si avrebbe

o anche, introducendo la mobilità ui = vi/E dei vari tipi di cariche (essendo E il campo elettrico),

.

La quantità che, in questa relazione, moltiplica E dipende dalla natura del mezzo in cui la c. si svolge: precisamente, essa è la conduttività σ del mezzo o, se si vuole, l’inverso della resistività ρ del mezzo in questione; cosicché è j = σE = E/ρ, relazione che costituisce la forma vettoriale della legge di Ohm. La quantità i = ʃ_S j ∙ n dS, vale a dire il flusso della densità di c. attraverso una sezione S di un circuito, ha il nome di intensità (istantanea) della c. nella sezione considerata; essa rappresenta la quantità di elettricità che nell’unità di tempo transita attraverso la sezione S, ed è suscettibile anche di una definizione diretta. Precisamente, i può essere definita come il rapporto tra la quantità di elettricità dq che in un intervallo di tempo infinitesimo dt transita attraverso S, e dt medesimo: cioè i = dq/dt. Unità di misura per l’intensità di c. è l’ampere (A), mentre per la densità di corrente è l’ampere al metro quadrato (A/m²).

Le linee del campo del vettore densità di c. coincidono, com’è evidente, con le linee di c. sopra definite. La proprietà fondamentale di tale vettore è espressa dalla relazione (equazione di continuità della c. elettrica): div j = − dρ/dt, dove ρ è la densità di carica e t il tempo. Tale relazione può leggersi dicendo che l’intensità complessiva della c. attraverso una superficie chiusa è eguale alla variazione nell’unità di tempo della carica elettrica complessivamente racchiusa dalla superficie (la relazione esprime cioè il principio di conservazione della carica elettrica). Il caso in cui la densità di carica non vari nel tempo lungo il circuito della c. è molto importante: è il caso delle cosiddette c. stazionarie, per le quali, dunque, il vettore densità di c. ha divergenza nulla, cioè è solenoidale, le linee di c. sono chiuse e l’intensità della c. è costante lungo il circuito, cioè non dipende dalla particolare sezione alla quale ci si riferisce.

C. di spostamento

In un mezzo di costante dielettrica assoluta ε nel quale agisca un campo elettrico variabile E, e quindi un campo di spostamento elettrico D = ε E, si instaura una c. di spostamento, la cui densità vale ∂D/δt. Gli effetti elettromagnetici di tale c., ipotizzati da J.C. Maxwell, sono stati poi verificati direttamente e indirettamente da esperienze con radioonde. Come c. totale dovremo allora intendere quella definita, punto per punto, dal vettore densità di c. totale J = j + ∂D/∂t o anche, ricordando la precedente relazione in termini di conduttività del mezzo, J = σE + ∂ (εE)/∂t. Linee di c. sono le linee del campo di tale vettore; posto che, com’è noto, è div D = ρ, dall’equazione di continuità sopra ricordata si deduce immediatamente che la densità di c. totale è un vettore solenoidale; conseguentemente, come non accadrebbe in generale se si considerassero le sole c. di conduzione, le linee di c. sono linee chiuse: come brevemente si usa dire, una c. elettrica (quando si consideri anche la eventuale c. di spostamento) è sempre chiusa. Dalla definizione del vettore D = ε₀ E + P (➔ dielettrico), dove ε₀ è la costante dielettrica assoluta del vuoto e P il vettore di polarizzazione, segue che contribuiscono alla c. di spostamento i due termini ε₀ ∂E/∂t e ∂P/∂t, il primo dei quali è presente anche nel vuoto e il secondo tiene conto del moto localizzato delle cariche di polarizzazione del dielettrico.

Tipi di corrente

Corrente alternata

C. variabile la cui intensità varia nel tempo con legge sinusoidale.

Corrente di buio

C. elettrica erogata da una cellula fotoelettrica o da un fotomoltiplicatore in assenza di illuminazione.

Corrente continua

C. la cui intensità non varia nel tempo.

Corrente di diffusione

C. costituita dal movimento di ioni che diffondono a causa di gradienti di concentrazione o di temperatura.

Corrente di Foucault

C. elettriche indotte che si generano in seno a un conduttore soggetto all’azione di un campo magnetico variabile oppure mobile entro un campo magnetico non uniforme. Trovano talora utili applicazioni (per es., nei forni a induzione e nei freni elettromagnetici), ma in generale costituiscono un inconveniente e provocano serie perdite di energia (di qui l’altra denominazione di c. parassite).

Corrente di regime

C. elettrica che scorre in un circuito durante le fasi non transitorie; in concreto, quella nella quale sono trascurabili le componenti (extracorrenti) derivanti dalla chiusura del circuito o da manipolazioni effettuate in esso.

Corrente diretta

In un circuito comprendente un elemento non simmetrico (per es., un raddrizzatore), quella che scorre nel verso di facile conduzione di quest’ultimo; la c. nel verso di difficile conduzione ha il nome di c. inversa.

Corrente elettronica

C. costituita da elettroni in moto.

Corrente fotoelettrica

C. elettrica la cui intensità è regolata da una cellula fotoelettrica.

Corrente ionica

C. costituita da ioni in moto.

Corrente termoelettrica

C. elettrica generata da una termocoppia.

Corrente vaganti

C. elettriche che, in linee tranviarie o ferroviarie a c. continua utilizzanti il binario come conduttore di ritorno, circolano in una fascia di terreno a cavallo del binario, larga anche qualche centinaio di metri e variamente profonda. Danno luogo a dannosi fenomeni di corrosione elettrochimica nei conduttori interrati in prossimità della linea.

Corrente variabile

C. la cui intensità varia nel tempo con legge qualsiasi.

Geofisica

Corrente marina

Per il moto d’assieme permanente di masse liquide marine in direzione costante ➔ corrènte marina.

Corrente a getto

C. aerea a getto, detta c. subtropicale, che spira al livello della tropopausa, con elevata velocità (varie centinaia di km/h) da O verso E, a una media latitudine (intorno a 30°) all’incirca al di sopra della zona di separazione tra le masse calde di origine subtropicale e le masse fredde di origine polare. Un’altra secondaria, meno intensa e detta c. subpolare, fluisce sempre al livello della tropopausa, a latitudine più alta, tra 50° e 60° (➔ circolazione). Le c. a getto, la cui scoperta è avvenuta intorno al 1946, hanno una grande importanza per le previsioni metereologiche: è stato infatti riscontrato come le grandi perturbazioni, in particolare i cicloni, si sviluppino al di sotto di esse, per cui l’individuazione del loro andamento può fornire utili informazioni per la previsione dello sviluppo delle perturbazioni.

Corrente di torbida

Movimento dovuto alla differenza di densità con il liquido circostante di masse fluide con elevato sedimento in sospensione. Queste c. sono flussi catastrofici che rappresentano un mezzo di trasporto e deposito di sedimenti in ambiente subacqueo, e in particolar modo marino (torbiditi).

Informatica

Programma corrente

È il programma in corso di elaborazione nel caso di procedure che prevedono l’esecuzione di programmi diversi. In ricerca operativa, il problema c. è quello in corso di risoluzione, nel caso di algoritmi che prevedono di operare su problemi diversi.

Musica

Danza vivace, in tempo ternario (misura 3/4) e formula ritmica iniziale in levare, diffusa in Italia e in Francia nel 16° e 17° sec. e successivamente anche in Germania. Compare spesso, idealizzata in musica strumentale pura, nella suite sei-settecentesca, ponendosi tra l’allemanda e la sarabanda.