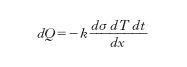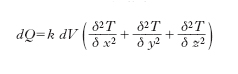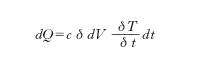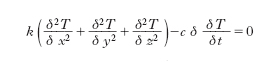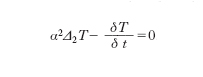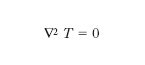conduzione

Fisica

In elettrologia, c. dell’elettricità nei mezzi materiali, l’insorgere nei mezzi stessi di correnti elettriche sotto l’azione di campi elettrici. Si presenta con modalità estremamente diverse a seconda della natura del campo e, soprattutto, a seconda della natura e delle condizioni fisiche del mezzo. La c. nei solidi è quella che offre la più grande varietà di fenomeni, non tutti ancora ben noti in dettaglio. Nei conduttori propriamente detti, i metalli, la c. è di tipo elettronico: la corrente è costituita dal moto di scorrimento, nel verso opposto a quello delle linee di forza del campo elettrico, di elettroni, gli elettroni di c., liberi di muoversi nell’ambito della banda di c. del metallo (➔ banda). Nei semiconduttori, la c. è affidata a elettroni (conduzione c. per elettroni) e a lacune (conduzione c. per lacune), forniti da atomi del semiconduttore o da atomi di impurità (➔ semiconduttore). Negli isolanti, infine, l’eventuale c., che peraltro avviene in regime di scarica distruttiva, è affidata a elettroni che passano, sotto l’azione di intensi campi, dalla banda di valenza a quella di conduzione. A parte questi casi, la c. nei solidi è dunque generalmente elettronica; la conducibilità (➔) è data dalla relazione σ=n e v/E, dove E è l’intensità del campo elettrico, e è la carica elettronica, n il numero degli elettroni di c. per unità di volume, v la velocità di scorrimento degli elettroni di c., cioè il valor medio della componente della velocità degli elettroni nella direzione del campo elettrico. Come accennato prima, la c. è fortemente influenzata dalle condizioni fisiche: l’aumentare della temperatura, per es., ostacola in genere la c. nei metalli e favorisce invece la c. nei semiconduttori e negli isolanti (per la c. alle basse temperature ➔ superconduzione). La c. nei metalli liquidi è ancora di tipo elettronico; è invece di tipo ionico nei conduttori elettrolitici e negli aeriformi.

In termologia, la c. del calore fra due punti di un materiale si verifica in presenza di una differenza di temperatura fra detti punti (il passaggio avviene dai punti a temperatura più alta verso quelli a temperatura più bassa); non è accompagnata da moto macroscopico di materia, ma si spiega con una trasmissione di energia tra costituenti elementari contigui (molecole, ioni ecc.). Lo studio matematico classico della c. è dovuto a J.-B.-J. Fourier (1822) e costituisce un significativo esempio di applicazione dell’analisi matematica alla fisica. Si applica quando, come effettivamente avviene nella maggior parte dei casi di interesse applicativo, l’incremento di temperatura fra due punti che distano fra loro di un libero cammino medio dei costituenti elementari del sistema è piccolo rispetto alla temperatura stessa (ci si riferisce qui alla temperatura assoluta, misurata in K). I fondamenti della teoria di Fourier sono i seguenti: se a un certo istante un punto qualunque di un corpo viene portato e mantenuto a una temperatura diversa, per es. superiore a quella degli altri punti, a partire da quell’istante ha inizio il fenomeno della propagazione. Si ha dapprima il cosiddetto periodo variabile, durante il quale la temperatura di ogni punto del corpo varia con il tempo; segue poi il periodo stazionario o permanente, caratterizzato dal fatto che la temperatura (diversa in generale da punto a punto) è in ciascun punto del corpo a ogni istante la medesima. Le superfici isotermiche, luoghi dei punti del corpo che si trovano a un certo istante alla stessa temperatura, sono nel periodo stazionario fisse e costanti. Il calore deve propagarsi secondo le traiettorie ortogonali alle superfici isotermiche, cioè secondo le cosiddette linee di flusso; la quantità di calore dQ, che nel tempuscolo dt passa da un elemento di una superficie isotermica σ′ a una temperatura T + dT a un elemento della vicinissima superficie isotermica σ a temperatura T, viene assunta proporzionale all’area ds dell’elemento che si considera, al salto dT di temperatura e al tempuscolo dt e inversamente proporzionale alla distanza dx fra i due elementi:

Il fattore k ha il nome di coefficiente di conducibilità termica interna (➔ conducibilità) e varia da sostanza a sostanza. La quantità di calore dQ complessivamente assorbita o ceduta dall’elemento di volume dV del corpo nel tempo dt è quindi data da

D’altra parte, a una somministrazione o sottrazione di calore dQ deve corrispondere una variazione di temperatura, legata a dQ dalla relazione

(c calore specifico, d densità). Uguagliando le due espressioni così ottenute per dQ si ha l’equazione

che più semplicemente si suole scrivere

essendo α²=k/(cd) e ∇² l’operatore di Laplace. Questa equazione differenziale alle derivate parziali è nota come equazione di Fourier. In regime stazionario, T non dipende più dal tempo, e si ha

L’integrazione dell’equazione di Fourier è possibile, per via analitica, solo in casi particolari, negli altri, per via numerica; per determinare in maniera completa la funzione T (x, y, z, t) bisogna assegnare le cosiddette condizioni al contorno.

Medicina

In fisiologia, il propagarsi dell’eccitamento lungo una fibra nervosa o dell’attività contrattile del miocardio, la quale è regolata dal sistema specifico di c., costituito dal nodo di Tawara e dal fascio di His (➔ cuore).