superconduzione
superconduzione In fisica, particolare tipo di conduzione, detto anche superconduttività, che alcuni elementi, alcuni composti e alcune leghe presentano nei riguardi della corrente elettrica.
Il fenomeno fu scoperto nel 1911 da H. Kamerlingh Onnes nel mercurio e, in breve tempo, confermato in varie altre sostanze.
Caratteri generali
La s. è caratterizzata dall’assenza di sensibili fenomeni dissipativi e quindi dalla circostanza che una corrente elettrica instauratasi in una di tali sostanze ha praticamente carattere permanente, cioè si mantiene costante in intensità, anche al cessare della causa che l’ha prodotta; questo tipo di conduzione, cui corrisponde una conduttività di valore grandissimo e, equivalentemente, una resistività praticamente nulla, si presenta se la temperatura è minore di una temperatura critica di s., o temperatura di transizione di s., variabile da sostanza a sostanza e, per una data sostanza, variabile con lo stato fisico, ma generalmente piuttosto bassa, dell’ordine di qualche kelvin.
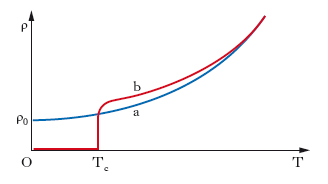
Mentre nei conduttori normali la resistività elettrica ρ diminuisce regolarmente al diminuire della temperatura termodinamica T sino a un valore limite ρ0 non nullo, nelle sostanze superconduttrici ρ cade bruscamente in corrispondenza della temperatura critica di s. Tc (fig. 1): l’esperienza indica in non più di 10−23 Ω∙m, che è un valore praticamente nullo, il valore della resistività per corrente continua di un superconduttore (quella del rame, che è un conduttore normale, è di circa 10−11 Ω∙m, poco sopra lo zero assoluto). La resistività di un superconduttore si mantiene pressoché nulla anche per correnti alternate sino a frequenze dell’ordine dei megahertz; per frequenze più alte la resistività aumenta lentamente finché, a frequenze dell’ordine di 1014 Hz (campo delle frequenze ottiche) e oltre, non vi è più superconduzione.
Elementi superconduttori
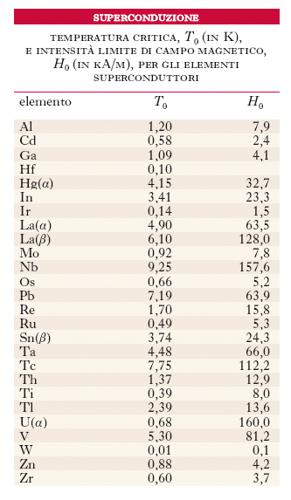
Sono superconduttori i 25 elementi indicati in tabella. Va osservato che alcuni elementi come Ba, Bi, Ge, Se, Te presentano s. se fortemente compressi e/o se sono allo stato amorfo in pellicola sottile; inoltre alcuni elementi sono superconduttori soltanto in una forma allotropica. Sono superconduttori numerosi elementi metallici: non però i metalli alcalini e nobili né quelli ferromagnetici e antiferromagnetici.
Presentano s. leghe e composti intermetallici di elementi superconduttori, e anche leghe e composti di elementi ordinari, specie se almeno uno dei componenti è vicino, nel sistema periodico degli elementi, a un elemento superconduttore: appartengono a quest’ultima categoria numerosi azoturi, boruri, carburi, idruri, siliciuri, solfuri. L’esperienza mostra che in campioni molto puri, non sollecitati in alcun modo, la transizione fra lo stato ordinario e quello superconduttore è rapidissima, avvenendo in un intervallo di temperature dell’ordine dei millesimi di kelvin; tale intervallo aumenta al diminuire della purezza e nei composti sale a 1 K e oltre. Altro notevole dato dell’esperienza, scoperto da Kamerlingh Onnes nel 1914 è che la s. viene meno se è presente un campo magnetico la cui intensità H superi un valore Hc, variabile da sostanza a sostanza, detto intensità critica; con buona approssimazione, si trovano le seguenti relazioni: Hc=H0[1−(T/Tc)2], Tc=T0[1–H/H0)]1/2, dove T0 è la temperatura critica di s. a campo nullo, cioè in assenza di campo magnetico, e H0 è l’intensità limite per T=0. In tabella sono riportati i valori di queste due costanti per gli elementi superconduttori.
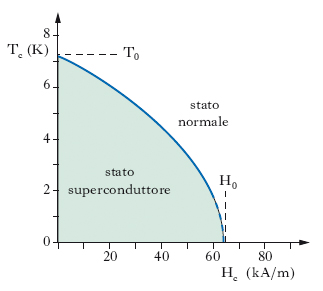
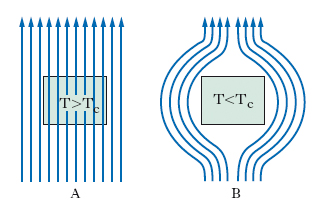
Nella fig. 2 è riportato l’andamento di Tc in funzione di Hc per il piombo: come si vede, è ben definito il campo di s., cioè il campo di valori di temperatura e di intensità di campo magnetico entro il quale si ha superconduzione. L’esistenza di un’intensità critica di campo magnetico dà conto del fatto che, in assenza di campo magnetico, la s. viene meno se l’intensità della corrente (in regime continuo) supera un certo valore: precisamente, questo valore è quello in corrispondenza al quale l’intensità del campo magnetico creato alla superficie del materiale dalla corrente è la predetta intensità critica. Particolarmente interessante al riguardo è il singolare comportamento magnetico associato alla transizione dallo stato normale a quello superconduttore: precisamente, e in ciò consiste l’effetto Meissner (1933), le linee di induzione magnetica vengono bruscamente espulse quando una sostanza, immersa in un campo magnetico, passa dallo stato normale (fig. 3A) allo stato superconduttore (fig. 3B). Questo comportamento corrisponde al fatto che l’induzione magnetica è nulla all’interno della sostanza superconduttrice; essendo l’induzione B legata all’intensità H e alla magnetizzazione M dalla relazione B=μ0H+M, con μ0 permeabilità assoluta del vuoto, nell’interno della sostanza è presente un campo di magnetizzazione tale che M=−μ0H; tale magnetizzazione è attribuibile a un sistema di correnti, fluenti alla superficie della sostanza, in uno spessore dell’ordine di 10–8 m (correnti di s.). Ricordando il legame fra intensità e magnetizzazione, M=μ0χH, con χ suscettività magnetica, da quanto precede risulta che per una sostanza superconduttrice la suscettività vale −1 (e la permeabilità relativa è dunque nulla): per tale motivo si parla di diamagnetismo perfetto associato alla superconduzione.
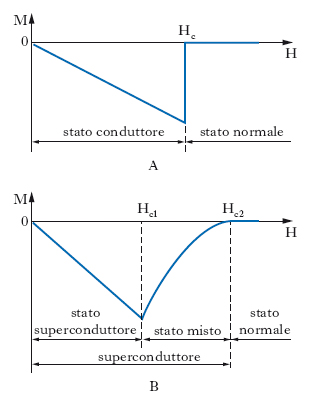
In effetti, soltanto certe sostanze, dette superconduttori del primo tipo, presentano tale diamagnetismo perfetto, schematizzabile con la curva di magnetizzazione della fig. 4A: si tratta in genere di elementi metallici. Esistono poi altri materiali, in genere metalli di transizione o leghe, detti superconduttori del secondo tipo, che presentano diamagnetismo perfetto sino a un valore di intensità magnetica Hc1 minore di Hc e a partire da un valore Hc2 maggiore di Hc; nel campo di valori di H fra l’intensità critica inferiore Hc1 e l’intensità critica superiore Hc2 si dice che la sostanza è in uno stato misto, o di transizione, come schematizzato nella fig. 4B.
Un importante fenomeno che ha notevole importanza per le teorie della s. è poi il cosiddetto effetto isotopico, consistente nel fatto che le costanti della s. variano, sia pure di poco, per isotopi diversi dello stesso elemento: precisamente, la temperatura di s. a campo nullo T0 è nei superconduttori più semplici dal punto di vista elettronico inversamente proporzionale alla radice quadrata del numero di massa dei vari isotopi. Questo effetto indica che nella s., ancorché si tratti di un fenomeno principalmente elettronico, è da attribuire un ruolo importante alle interazioni ioni-elettroni, o se si vuole, reticolo-elettroni: non per nulla la s. riguarda mediocri conduttori elettrici, cioè sostanze caratterizzate appunto da elevate interazioni fra il reticolo e gli elettroni di conduzione.
Interpretazione del fenomeno
L’interpretazione microscopica del fenomeno della superconduttività è stata data dalla cosiddetta teoria BCS, dal nome degli studiosi (J. Bardeen, L.N. Cooper, J.R. Schrieffer) che, nel 1957, l’hanno proposta. Questi autori, partendo da suggerimenti in parte già avanzati da altri, hanno fornito una rappresentazione di un sistema di elettroni nello stato superconduttore che ha permesso di spiegarne le proprietà fondamentali, come l’annullarsi della resistività, l’effetto Meissner e tutta una serie di effetti già osservati, oltre a prevedere altri effetti, riscontrati in seguito. Lo stato superconduttore è uno stato fortemente correlato di elettroni che tendono a legarsi in coppie su distanze dell’ordine di 1 μm (un migliaio di distanze interatomiche nel cristallo), con una vita media limitata e un guadagno energetico, Ec, dell’ordine di 10–4 eV per ogni coppia di elettroni rispetto allo stato normale. Tali coppie, dette coppie di Cooper, si formano come conseguenza dell’interazione fra gli elettroni e le oscil;lazioni reticolari (fononi), come d’altron;de è segnalato dall’effetto isotopico.
Un elettrone che si muove nel cristallo dà luogo, lungo la sua traiettoria, a un addensamento dinamico degli ioni, cioè a delle distorsioni del reticolo, che decadono con un tempo caratteristico dell’ordine di 10–12 s. Queste distorsioni provocano fluttuazioni di carica positiva che, quindi, possono attirare altri elettroni. A causa dell’invarianza per inversione temporale delle equazioni dinamiche che descrivono il sistema di elettroni e ioni, esiste un secondo elettrone che si muove con quantità di moto opposta a quella del primo e che può sfruttare al massimo l’attrazione, costituendo una coppia controrotante con il primo. Il principio di esclusione di Pauli limita ai soli elettroni in stati vicini alla superficie di Fermi la possibilità di formare coppie. Un’altra conseguenza del carattere ‘ritardato’ di questa interazione è che gli elettroni si trovano sufficientemente lontani fra loro perché gli altri elettroni riescano a schermare con efficacia la repulsione coulombiana, che risulta considerevolmente ridotta: l’interazione complessiva è, quindi, un’attrazione tra la coppia di elettroni. La particolare forma del modello BCS favorisce l’accoppiamento in uno stato in cui i due elettroni hanno spin opposti.
Meccanismi come quello descritto possono essere mediati anche da altri tipi di eccitazioni, come gli eccitoni e i magnoni. Alla base della s. sta il fatto che le coppie di elettroni, avendo spin totale intero, si comportano come bosoni, obbediscono cioè alla statistica di Bose-Einstein: quando la temperatura è sufficientemente bassa (kT≪Ec) da consentire la formazione delle coppie di Cooper, queste, essendo bosoni, possono dar luogo a un fenomeno analogo alla condensazione di Bose-Einstein, in seguito alla quale una frazione finita di esse va a occupare il più basso livello di energia possibile (➔ statistica).
Tutti i fatti sperimentali della s. trovano soddisfacente spiegazione nell’ambito della teoria BCS. In particolare, la teoria BCS prevede che il flusso ϕ del campo magnetico generato da un anello superconduttore deve essere quantizzato: ϕ=nh/q, con n intero positivo, h co;stante di Planck, q carica elettrica di una coppia di Cooper (pari al doppio della carica elettronica); questo effetto è stato osservato sperimentalmente per la prima volta nel 1961. Inoltre, quando due materiali superconduttori sono separati da un sottile strato di isolante (10-100 Å) in modo da formare una giunzione, è possibile un passaggio di coppie di elettroni attraverso tale barriera per effetto tunnel: tale fenomeno, previsto da B.D. Josephson e detto pertanto effetto Josephson, è stato osservato sperimentalmente per la prima volta nel 1962.
S. ad alta temperatura critica
Specialmente in considerazione degli aspetti applicativi, si è a lungo tentato di trovare materiali superconduttori con temperatura critica elevata e in grado di sostenere valori elevati di supercorrente in presenza di campi magnetici molto intensi. Sono state individuate varie famiglie di ossidi di rame – e per questo motivo questi nuovi superconduttori ad alta temperatura critica sono detti cuprati – con temperature critiche sempre maggiori: la famiglia La2–xSrxCuO4 (con 0<x<0,3 e T0 massima di circa 42 K per x=0,15), la famiglia YBa2Cu3O6+x (con 0,6<x<1 e T0 massima di circa 92 K per x=1) e vari composti Tl(Bi)-Ca-Sr(Ba)-Cu-O, con T0=105-125 K. La temperatura critica massima attualmente accertata è di circa 135 K per composti di mercurio (HgBa2CunO2n+2+xδ, n=1, 2, 3), che mostrano un marcato aumento di T0 (fino a circa 150 K) indotto dalla pressione.
Applicazioni della superconduzione
Sono state sviluppate le applicazioni della s. alla realizzazione di elettromagneti (per acceleratori e rivelatori di particelle elementari, per macchine a plasma a contenimento magnetico ecc.) in grado di generare campi dell’ordine di 10 T in volumi dell’ordine dei metri cubi. Notevoli sono stati anche gli studi, culminati nella realizzazione di prototipi, relativi all’impiego della s. in turboalternatori per centrali di grandi dimensioni (oltre 1000 MW), cavi per il trasporto di energia elettrica, motori in corrente continua per potenze superiori a 100 MW. Vi è inoltre allo studio l’impiego di magneti superconduttori per ottenere la levitazione magnetica di veicoli terrestri ad alta velocità. Per le applicazioni della s. basate sull’effetto Josephson ➔ SQUID.