reticolo

Biologia

In biologia cellulare, r. endoplasmatico (o endoplasmico), sistema di cavità delimitate da membrane, presente nel citoplasma di tutte le cellule. È costituito da una membrana formata da un unico foglietto continuo, molto ripiegato, che racchiude un unico sacco chiuso detto lume del r. endoplasmatico e che rappresenta più della metà delle membrane totali della cellula. Al microscopio elettronico si distinguono due regioni funzionalmente distinte del r. endoplasmatico, il r. endoplasmatico liscio e il r. endoplasmatico ruvido: il primo è corredato di ribosomi situati sul lato citoplasmatico della membrana ed è organizzato in pile di sacchi appiattiti dette cisterne; il secondo è privo di ribosomi ed è formato da una rete tridimensionale di sottili tubuli. Il r. endoplasmatico ruvido, pur essendo presente in tutte le cellule, eccettuati gli spermatozoi, è particolarmente abbondante sia nelle cellule specializzate nella secrezione di proteine sia nelle cellule dove avviene una sintesi massiva di membrane. Il r. endoplasmatico liscio non partecipa invece alla sintesi proteica e costituisce in quasi tutte le cellule una regione, chiamata anche r. di transizione, dalla quale si staccano vescicole contenenti le proteine e i lipidi neosintetizzati, che vengono così trasportati nei vari comparti cellulari. Le proteine sintetizzate nella cellula che entrano nel circuito distributivo del r. endoplasmatico hanno una serie di possibili destinazioni cellulari: alcune sono secrete all’esterno della cellula, altre rimangono ancorate alla membrana del r., altre ancora sono dirette alla membrana nucleare, all’apparato di Golgi, ai lisosomi, alla membrana plasmatica e formano i vari organelli intracellulari.

fig. 1A

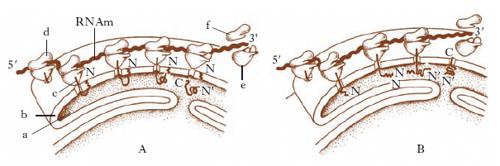
Il processo di inserimento nel r., di norma, viene guidato da una sequenza-segnale localizzata all’estremità N-terminale delle proteine. Nel 1975 G. Blobel, B. Dobberstein e P. Walter formularono l’ipotesi del ‘segnale’, successivamente confermata da numerose evidenze sperimentali. Secondo tale ipotesi, gli RNAm che codificano queste proteine sono dotati di un segmento situato all’inizio della sequenza codificante che specifica un segnale di tropismo per il r. endoplasmatico. Il ribosoma sul quale avviene la sintesi del polipeptide con una sequenza-segnale per mezzo della cosiddetta SRP o particella di riconoscimento del segnale, si lega a recettori specifici situati sulla membrana del r. endoplasmatico; la sequenza-segnale, che ha caratteristiche idrofobiche, penetra nella membrana. Con il procedere della sintesi proteica, la catena polipeptidica in allungamento si spinge attraverso la membrana. Se la proteina è destinata alla secrezione o ad altri compartimenti cellulari, l’intera catena polipeptidica a valle del segnale passa completamente attraverso la membrana e finisce nel compartimento interno del r. (fig. 1A); se invece la proteina è destinata a diventare una proteina transmembrana, uno o più segnali di arresto del trasferimento situati all’interno della proteina stessa determinano il blocco dello scorrimento attraverso la membrana (fig. 1B). Una volta stabilita la destinazione della proteina, un enzima (peptidasi del segnale) stacca il polipeptide segnale che viene successivamente degradato. R. sarcoplasmatico Guaina di vescicole appiattite e anastomizzate, derivate dal r. endoplasmatico, che circonda le miofibrille. R. microtrabecolare Rete tridimensionale di sottili filamenti proteici che si osservano al microscopio elettronico ad alto voltaggio in cellule coltivate in vitro, dopo un trattamento veloce di criodecapaggio.

Fisica

Ottica

fig. 2A

R. di diffrazione

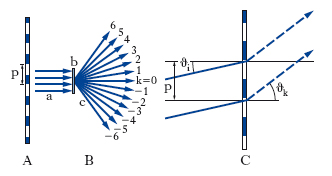
Dispositivo che sfrutta il fenomeno della diffrazione. Nella sua forma tipica è costituito da uno schermo opaco nel quale è praticato un gran numero di fenditure rettilinee, parallele ed equidistanti (tratti del r.); passo (o periodo, o costante) del r. è la distanza p (fig. 2A) fra due tratti contigui; frequenza del r. è l’inverso del passo, cioè il numero di tratti per unità di lunghezza (a seconda dell’uso cui il r. è destinato, la frequenza può andare da una decina a oltre un migliaio di tratti per millimetro). Un fascio di raggi luminosi monocromatici paralleli a (fig. 2B) che incida su un r. b viene scomposto, per fenomeni di diffrazione e interferenza, in una serie di fasci diffratti c, che si propagano in direzioni determinate dalla lunghezza d’onda λ, dal passo p del r. e dall’angolo di incidenza dei raggi sul reticolo. Precisamente, per il principio di Huygens, i punti delle porzioni dei fronti d’onda che emergono dalle fenditure possono essere pensati come sorgenti di onde sferiche elementari; considerando punti a distanza così grande del r. da potersi ammettere che le onde emananti dalle varie fenditure e giungenti in quei punti procedano tutte nella medesima direzione, è facile vedere che esistono delle direzioni nelle quali i campi provenienti dalle varie fenditure si compongono tutti in fase, dando quindi luogo a massimi di interferenza costruttiva.

Detto ϑ _i (fig. 2C) l’angolo di incidenza del fascio e supponendo che il piano di incidenza sia ortogonale alle fenditure, gli angoli ϑ_k che individuano le direzioni in questione, lungo le quali è dunque concentrata la radiazione diffratta, sono fissati dalla condizione che la differenza di cammino fra onde provenienti da punti corrispondenti di due fenditure contigue sia pari a un multiplo intero della lunghezza d’onda λ della radiazione usata. Come si può ricavare dalla fig. 2C, gli angoli ϑ_k sono quelli che soddisfano la relazione:

[1] formula

con k=0, ±1, ±2, ... e con p passo del reticolo. Si noti che per k=0 è ϑ₀=ϑ_i; ciò significa che una delle componenti del campo diffratto è un’onda piana che procede nella stessa direzione di quella incidente: a tale onda si dà il nome di onda di ordine zero. Per k=±1 si hanno altre due onde piane diffratte, una a destra e una a sinistra di quella di ordine zero (fig. 2B), che prendono il nome di onde del primo ordine; analogamente, si parla di onde del secondo ordine per k=±2, e così via. Al di sopra di un certo valore k si avrebbe senϑ_k>1: le onde diffratte corrispondenti a tale assurdo matematico sono onde evanescenti, cioè onde non osservabili, che si propagano nel piano del r. e che si attenuano esponenzialmente in direzione ortogonale a esso, così rapidamente da ridursi ad ampiezza trascurabile entro poche lunghezze d’onda. Per p<λ e per incidenza normale (per incidenza radente se p<λ/2) la sola onda emergente dal r. è quella di ordine zero. In quest’ultimo caso, poiché l’intensità dell’onda incidente sta a quella dell’onda di ordine zero secondo un fattore pari alla trasparenza media del r., il dispositivo si comporta come un assorbitore uniforme, con trasparenza pari alla trasparenza media.

La disposizione tipica corrispondente allo schema di principio ora illustrato comprende una sorgente lineare (costituita da una fenditura rettilinea parallela ai tratti del r., illuminata da una sorgente monocromatica) posta nel piano focale di una lente convergente (collimatore) e un cannocchiale che raccoglie la luce diffratta dal r.: nel campo dell’oculare si vede una figura di diffrazione costituita da una serie di righe luminose (leggermente incurvate), immagini della sorgente corrispondenti alle onde diffratte dei vari ordini.

fig. 3

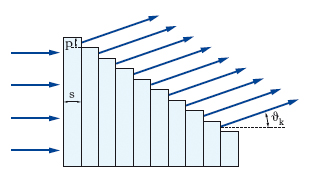
I r. a fenditure lineari appartengono alla categoria dei r. a tratti rettilinei, o r. lineari, operanti per trasmissione (r. diottrici); vi sono infatti r. a tratti circolari o r. circolari, e r. operanti per riflessione (r. catottrici): a questi ultimi, ottenibili, per es., scalfendo a righe parallele una superficie lucida, possono essere estese le considerazioni già fatte per i r. a fenditure. Ancora in relazione al modo di operare, si distinguono r. che influenzano le onde incidenti modificandone l’ampiezza (r. d’ampiezza), r. che, introducendo un cammino ottico variabile periodicamente con il passo, modificano la fase (r. di fase) e infine r. che modificano sia l’ampiezza sia la fase delle onde incidenti (r. d’ampiezza e di fase). È un r. d’ampiezza, per es., quello a fenditure lineari della fig. 2C, mentre un esempio di r. di fase è costituito dal r. a gradinata, di Michelson. La dipendenza della direzione dei fasci diffratti dalla lunghezza d’onda, sintetizzata dalla [1], fa sì che, se la radiazione incidente non è monocromatica, il fascio diffratto di un ordine qualunque è costituito dalla sovrapposizione di vari fasci, che si propagano in direzioni differenti, ognuno dei quali corrisponde a una delle componenti monocromatiche della radiazione incidente: come dire che il r. fornisce una serie di spettri di quest’ultima, e ciò è alla base dell’applicazione che i r. hanno in spettroscopia. R. sostanzialmente analoghi a quelli ottici sono usati nel campo delle radioonde (per es., r. filari per microonde). R. a gradinata, di Michelson R. di fase, per trasmissione (o riflessione), costituiti dalla sovrapposizione di un certo numero N di lastre di vetro lavorate otticamente e sfalsate tra loro in modo da formare una gradinata (fig. 3). Il passo è dell’ordine del millimetro e quindi si ha diffrazione solo sotto angoli molto piccoli. Nel caso di funzionamento in trasmissione con incidenza normale, la condizione di interferenza costruttiva per angoli ϑ piccoli (cosϑ ≅1) è:

fig. 4A

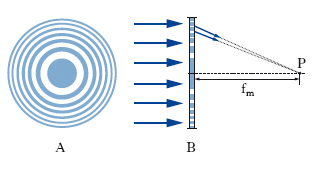
dove s è lo spessore di un gradino, n è l’indice di rifrazione del vetro. L’ordine nell’intorno del quale si lavora è allora k=s(n−1)/λ e può essere molto elevato (diverse migliaia); pertanto il potere risolutivo kN raggiunge valori molto alti anche con solo qualche decina di lastre; se si argentano le lastre e si lavora in riflessione, il potere risolutivo aumenta ulteriormente. R. di Soret R. circolari, detti anche r. a zone o r. zonati (o lastre a zone di Fresnel), d’ampiezza, per trasmissione, costituiti da corone circolari concentriche, alternativamente trasparenti e opache (fig. 4A), i cui raggi r crescono secondo la relazione

dove n è il numero d’ordine della corona, a partire dal centro. Se il r. è illuminato da un’onda piana monocromatica che vi incide normalmente, nei punti P dell’asse a una distanza f_m dal centro del r. (fig. 4B) che soddisfi la relazione f_m=r₁²/(2λm), con m intero positivo, le onde provenienti da vari tratti del r. si compongono in fase dando luogo a massimi di intensità luminosa, con una concentrazione di luce paragonabile a quella che si ha nel fuoco di una lente convergente. È per questo motivo che il r. zonale viene anche detto lente a focale multipla, le lunghezze focali essendo date dalla formula precedente (si tratta, ovviamente, di una lente fortemente cromatica). Questa analogia con le lenti può estendersi anche a sorgenti estese a distanza finita dal reticolo.

Teorie quantistiche su reticoli

Teorie basate sulla discretizzazione dello spazio-tempo come schema di regolarizzazione per teorie di campo quantistiche. Infatti, la discretizzazione dello spazio-tempo, mediante l’introduzione di un r. di punti, costituisce uno schema di regolarizzazione per teorie di campo quantistiche che permette lo studio di fenomeni per i quali la teoria delle perturbazioni risulta inadeguata. In questi casi, infatti, l’introduzione del r. rende possibile l’uso di tecniche di approssimazione non perturbativa quali, per es., l’espansione d’accoppiamento forte (o ad alta temperatura) o le simulazioni Montecarlo. Le simulazioni numeriche, grazie all’avvento di superelaboratori o di elaboratori espressamente progettati per le simulazioni Montecarlo delle teorie di campo (elaboratori dedicati), hanno consentito notevoli progressi, rendendo possibile lo studio di problemi altrimenti inaccessibili; le tecniche numeriche sono, per es., correntemente utilizzate per calcolare quantità d’interesse fenomenologico nella fisica degli adroni partendo dalla teoria fondamentale delle interazioni forti (cromodinamica quantistica, ➔ forti, interazioni).

Geografia

In geomorfologia, il r. idrografico rappresenta l’insieme dei corsi d’acqua che, scorrendo e confluendo tra loro in una determinata regione, danno origine a un sistema costituito da un corso d’acqua principale e da tutti i suoi affluenti. L’area all’interno della quale si sviluppa il r. idrografico prende il nome di bacino idrografico. Un r. idrografico costituisce in sostanza una rete dove i tributari più piccoli confluiscono in quelli più grandi, evidenziando così un grado di gerarchizzazione del r. stesso, la misura del quale può essere valutata attraverso la definizione dell’ordine dei segmenti fluviali, criterio introdotto inizialmente da R. Horton e in seguito rielaborato da A.N. Strahler. Procedendo verso valle, l’ordine dei segmenti fluviali aumenta; parallelamente si ha una diminuzione del numero delle aste fluviali principali, mentre aumentano la loro lunghezza e la loro area di drenaggio.

fig. 5A

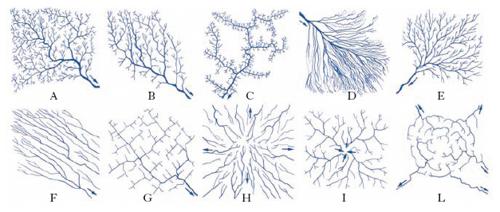
Lo studio dei r. idrografici può essere affrontato da un punto di vista sia quantitativo sia descrittivo. Nel primo caso può essere calcolata una serie di indici: a) fittezza del r. idrografico, o densità di drenaggio, rapporto fra la somma delle lunghezze di tutti i segmenti fluviali e l’area del bacino idrografico; b) frequenza areale dei segmenti idrografici, rapporto fra il numero totale dei segmenti fluviali e l’area del bacino idrografico; c) rapporto di confluenza, o di biforcazione, rapporto espresso dalla relazione R_b=N_u/(N_u+1), dove N_u rappresenta il numero di segmenti idrografici di ordine u in un determinato bacino fluviale. Da un punto di vista descrittivo si possono riconoscere diverse configurazioni geometriche (pattern) di r. idrografici, che variano da bacino a bacino in funzione della litologia, dell’assetto tettonico dell’area, del diverso grado di erodibilità e permeabilità dei terreni, dell’orografia ecc. I principali tipi di pattern sono: a) pattern dendritico (fig. 5A): r. che presenta una forma arborescente, con le aste fluviali che si dispongono in modo casuale; caratterizza le aree con terreni omogenei e impermeabili a limitata acclività; b) pattern subdendritico (fig. 5B): r. in cui alcuni rami fluviali hanno direzioni preferenziali, evidenziando così la presenza di fratture; c) pattern pinnato (fig. 5C): r. caratterizzato dall’avere le aste fluviali secondarie di limitata lunghezza; si rinviene in aree con terreni omogenei, impermeabili e a morfologia pianeggiante; d) pattern divergente (fig. 5D): r. che presenta un ramo principale dal quale si dipartono più collettori secondari fino a formare una sorta di ventaglio; caratterizza le aree delle conoidi alluvionali; e) pattern convergente (fig. 5E): r. in cui le aste secondarie confluiscono in quella principale; si riscontra in terreni poco permeabili e a sensibile acclività; f) pattern parallelo (fig. 5F): r. caratterizzato dall’avere le aste fluviali subparallele tra di loro; si sviluppa su terreni impermeabili a sensibile acclività; g) pattern angolato (fig. 5G): r. che si riscontra in un’area interessata dalla presenza di numerose fratture, di cui i corsi d’acqua seguono l’andamento; un particolare tipo di questo r. è quello chiamato a graticcio; h) pattern centrifugo (fig. 5H): r. che si imposta generalmente su rilievi isolati, a forma di cono o di cupola come un vulcano, un domo tettonico ecc.; i) pattern centripeto (fig. 5I): r. in cui le diverse aste fluviali convergono verso una stessa area che può essere rappresentata da una depressione tettonica, carsica, vulcanica ecc.; l) pattern anulare (fig. 5L): r. in cui le diverse aste fluviali hanno degli andamenti concentrici; si sviluppa in zone con morfologia cupoliforme, a gradinate, che testimoniano la presenza di rocce a differente grado di erodibilità. Le caratteristiche di un r. idrografico dipendono, oltre che dalla geomorfologia del luogo, anche dal clima locale, che condiziona lo sviluppo di un r. e ne controlla la densità di drenaggio. Sotto questo punto di vista si possono distinguere: a) regioni esoreiche, tipiche delle zone umide e caratterizzate da un r. idrografico permanente e gerarchizzato, attraverso il quale le acque vengono convogliate fino al mare; b) regioni endoreiche, tipiche dei climi semiaridi: hanno un r. idrografico con corsi d’acqua a regime temporaneo che non sfociano in mare, ma confluiscono in bacini lacustri o in aree acquitrinose dove le stesse acque si perdono per infiltrazione sotterranea e per evaporazione; c) regioni areiche: caratterizzano le aree con clima arido dove i corsi d’acqua, che hanno un regime occasionale, confluiscono spesso in vaste piane dove le acque si perdono per evaporazione. Il r. idrografico è quasi sempre ereditato da una precedente morfologia, sviluppata in un clima differente.

Matematica

Si chiama r. un insieme R provvisto di due operazioni binarie chiamate intersezione (simbolo ⋃ o anche ⋀) e unione (indicata con ⋂ o con ⋁) e che verifica le seguenti proprietà:

Si nota che i due assiomi di ciascuna delle 4 coppie di proprietà si ottengono l’uno dall’altro scambiando le operazioni di unione e di intersezione: segue da ciò il principio di dualità della teoria dei r., secondo il quale in ogni teorema T sui r. si possono scambiare tra loro le due operazioni citate ottenendo un altro teorema T′ anch’esso valido, detto appunto duale di T.

In aritmetica costituiscono un r. i numeri naturali quando si assumano come intersezione e unione di 2 numeri il loro massimo comune divisore e, rispettivamente, il minimo comune multiplo (o anche viceversa). Stretti collegamenti intercorrono fra la nozione di r. e quella di insieme parzialmente ordinato. Infatti, se in un r. R si pone x≤y, qualora risulti x⋂y=y si trova che la relazione espressa dal simbolo ≤ attribuisce a R un ordinamento parziale. Viceversa, sia E un insieme provvisto di un ordinamento parziale; fissati due qualsiasi elementi x, y, di E, si considerino i sottoinsiemi E′ E″ di E costituiti rispettivamente dagli elementi di E che nell’ordinamento considerato precedono sia x, sia y e da quelli che seguono entrambi. Si supponga che E′ abbia un elemento, indicato con x⋃y, che segue tutti gli altri elementi di E′ e contemporaneamente E″ abbia un elemento denotato con x⋂y, precedente tutti gli altri elementi di E″: in tal caso l’insieme E è un r. rispetto alle due operazioni ⋃, ⋂ ora introdotte.

fig. 6

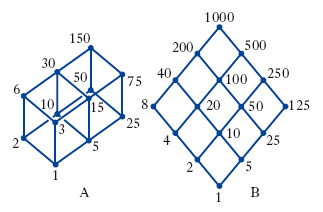
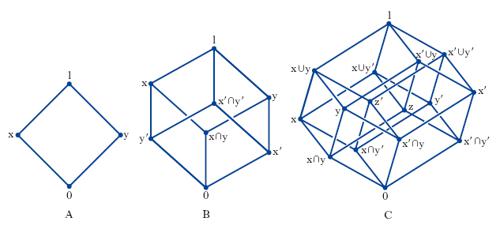
Se un r. è costituito da un numero finito di elementi, la sua struttura algebrica si può efficacemente visualizzare mediante uno schema grafico. Si dice che un elemento y di un r. «copre» o anche «è precedente immediato» di un elemento x se esso è precedente x e non esiste nessun elemento z precedente x ma a sua volta preceduto da y. Ciò premesso, il diagramma di un r. si costruisce rappresentando con un punto ogni elemento del r. e congiungendo con un segmento due elementi qualora uno di essi copra l’altro. In fig. 6 sono rappresentati, «rispettivamente in A e in B», i r. dei divisori di 150 e di 1000.

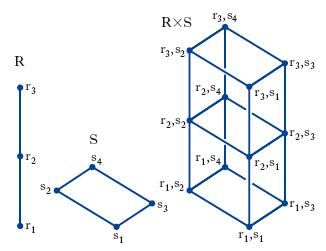
Dato un r. R si chiama sottoreticolo di R ogni sottoinsieme R′ di R che sia a sua volta un r. rispetto alle operazioni ⋂ e ⋃ definite in R. Per es., il r. dei divisori di 50 è un sottoreticolo del r. dei divisori di 100. La nozione di prodotto diretto di r. consente di ottenere nuovi r. a partire da due o più r. assegnati. Siano R, S due r.; l’insieme delle coppie ordinate (r, s) con r∈R, s∈S costituisce un nuovo r. T (che si chiama prodotto diretto di R, S e si denota con R×S) se in tale insieme si introducono le operazioni di unione e di intersezione al modo seguente:

fig. 7

In fig. 7 sono indicati gli schemi di due r. R ed S e del loro prodotto diretto. R. distributivo R. nel quale valgono le seguenti due leggi (duali tra loro ed equivalenti):

fig. 8

La nozione di r. modulare (o r. di Dedekind) è una generalizzazione di quella di r. distributivo: si chiama r. modulare ogni r. nel quale se x ≥ z allora, per ogni y, risulta x ⋃ (y ⋂ z) = (x ⋃ y) ⋂ z. Si dimostra che un r. è modulare se non contiene sottoreticoli pentagonali come quello della fig. 7. I r. modulari costituiscono una classe di r. di notevole interesse: sono, per es., modulari il r. dei sottogruppi di un gruppo abeliano, il r. degli ideali destri (o sinistri) di un anello ecc. R. completo R. nel quale ogni sottoinsieme di elementi ha un estremo inferiore e un estremo superiore. In tali r. si possono introdurre le nozioni di limite e di convergenza. R. complementato R. nel quale esistono due elementi, indicati con 0 e 1 tali che per ogni elemento x sia 0 ≤ x ≤ 1 e inoltre che a ogni x si possa associare un x′ (complemento di x) avente la proprietà che x ⋃ x′ = 0, x ⋂ x′ = 1. Un r. distributivo e complementato è un’algebra di Boole. Le algebre di Boole godono di molte proprietà specifiche; per es., il complemento di x ⋃ y è uguale a x′ ⋂ y′ e, dualmente, il complemento di x ⋂ y è x′⋃ y′. Un’algebra di Boole è prodotto diretto di r. costituiti da due elementi: nella fig. 8 sono indicati i diagrammi delle algebre di Boole di 4, 8, 16 elementi.

Medicina

R. venoso

Dilatazione di vene sottocutanee anastomizzate a rete di una determinata regione corporea, che si instaura quando una qualsiasi condizione patologica ostacoli il corrispondente circolo venoso profondo. Costituisce un circolo di compenso (o circolo collaterale) atto a scaricare nella circolazione tributaria il sangue ristagnante a monte dell’ostacolo.

Zoologia

La seconda cavità dello stomaco concamerato dei Ruminanti, derivata da una dilatazione esofagea e comunicante sia con il rumine, sia con l’esofago e l’omaso, in cui il cibo viene separato in parti grossolane (rinviate alla bocca) e parti già fini e sminuzzate (incanalate verso l’omaso). Il nome deriva dalla struttura ad alveoli delle pliche interne.

La reticolite è il processo infiammatorio a carico del r.; le reticoliti traumatiche sono dovute a ingestione di corpi acuminati, richiedono spesso l’intervento chirurgico.