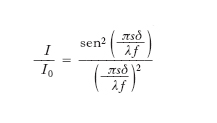diffrazione

Fenomeno che si determina nella propagazione di grandezze di natura ondulatoria, consistente nel fatto che se vi sono ostacoli di qualsiasi genere sul cammino di un’onda (corpi opachi più o meno estesi, diaframmi forati ecc.) l’energia dell’onda si ripartisce al di là dell’ostacolo pervenendo anche in punti ‘in ombra’, nei quali essa non potrebbe giungere se la propagazione avvenisse per raggi rettilinei. I fenomeni di d., insieme a quelli d’interferenza (➔) e di polarizzazione (➔), evidenziano il carattere ondulatorio delle radiazioni che li producono.

1. D. della luce

Il fenomeno fu osservato e descritto per la prima volta, in un’opera pubblicata postuma nel 1665, dal gesuita F.M. Grimaldi. Successivamente, fra l’alterno affermarsi delle teorie ondulatorie e corpuscolari sulla natura della luce, hanno contribuito alle ricerche sulla d. celebri fisici, fra cui T. Young, A.-J. Fresnel, J. Fraunhofer.

fig. 1A

fig. 2

fig. 3

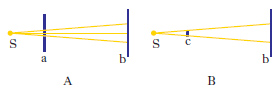
Quando un fascio di raggi luminosi, monocromatici o no, provenienti da una sorgente (puntiforme) S, attraversa un foro di piccolo diametro (qualche decimo di millimetro, per es.) praticato in uno schermo opaco a, si forma su uno schermo b posto a distanza opportuna da S (1-2 m) non un dischetto illuminato, circondato da un’ombra netta (come indicato in fig. 1A e come dovrebbe verificarsi ammettendo valide le leggi della propagazione rettilinea), ma una figura di d. costituita da aloni o frange di d., concentriche, alternativamente chiare e scure (fig. 2). Se si toglie a e al suo posto si mette un dischetto opaco c (fig. 1B), invece dell’ombra che ci si aspetterebbe, si vede formarsi su b una figura di d. (v. fig. 3) costituita da una zona d’ombra centrale che può presentare una luminosità puntiforme verso il centro, e da aloni periferici.

fig. 4

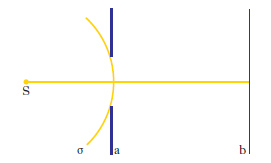
Di questi e degli altri svariatissimi fenomeni di d. che si possono avere in corrispondenza alle varie forme dell’ostacolo (spigoli, griglie, fili opachi, fenditure multiple ecc.) si riesce a dare una soddisfacente spiegazione sulla base del principio di Huygens. Per esso, in una propagazione per onde, ciascun punto della superficie d’onda σ_t relativa all’istante generico t diviene sorgente di onde sferiche secondarie, e la superficie d’onda relativa a un istante successivo t+dt coincide con l’inviluppo di tutte le onde secondarie emesse dagli elementi di σ_t. Un ostacolo presente sul cammino di un’onda intercetta una porzione più o meno vasta della superficie d’onda; naturalmente soltanto i punti della parte non intercettata possono divenire centri di emissione di nuove onde e l’andamento successivo non è più quello che si avrebbe nella propagazione libera. Si consideri, per es., la situazione illustrata nella fig. 4: σ è la superficie d’onda della luce, monocromatica, emessa dalla sorgente puntiforme S, incidente su un’apertura praticata nello schermo opaco a, mentre b è lo schermo su cui si raccoglie la luce che emerge dall’apertura. L’ampiezza E dell’onda (e quindi l’intensità, proporzionale al quadrato di E) nei vari punti di b è quella che risulta dall’interferenza (➔) delle onde sferiche provenienti dai vari punti della porzione di σ non schermata da a.

Particolarmente interessante, per le applicazioni pratiche cui dà luogo, è il caso di un diffrattore costituito da molte fenditure identiche, parallele ed equidistanti, cioè il caso del reticolo di d. (➔ reticolo). Poiché la distanza tra le frange di d. è funzione di λ, le figure di d. si presentano con un forte cromatismo: se la luce è policromatica, e in particolare bianca, le frange di d. appaiono colorate dei colori dell’iride.

fig. 5

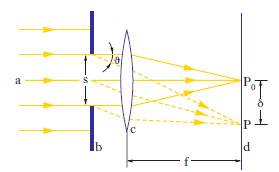
D. alla Fraunhofer Fenomeno di d. (detto anche d. in campo lontano) che si verifica quando sia la sorgente sia lo schermo sono a distanza infinitamente grande dall’ostacolo diffrangente: le onde incidenti sono piane e la figura di d. viene esaminata ponendo lo schermo nel piano focale di una lente convergente che raccoglie la luce diffratta. La trattazione analitica e l’andamento stesso dei fenomeni di d. sono più semplici di quelli relativi ai casi di schermo a distanza non grandissima, che si usa indicare come fenomeni di d. alla Fresnel o in campo vicino. La fig. 5 illustra la disposizione tipica per la d. alla Fraunhofer. Un fascio di raggi paralleli a incide normalmente su uno schermo b, nel quale è praticata una fenditura, per es. rettangolare, larga s e lunga t; accostata allo schermo diffrangente è una lente convergente, c, nel cui piano focale è posto uno schermo, d. Secondo l’ottica geometrica, la luce emergente dall’apertura dovrebbe convergere semplicemente in P₀; in realtà, in base al principio di Huygens, vanno considerate tutte le onde secondarie provenienti dai vari punti dell’apertura: in P, per es., convergono, interferendo tra loro, tutti i raggi secondari inclinati di un angolo ϑ rispetto alla direzione dei raggi incidenti. Si dimostra che l’intensità della luce in P risulta proporzionale al quadrato dell’ampiezza di vibrazione delle onde incidenti e al quadrato dell’area dell’apertura; se, come del resto si fa anche nella trattazione della d. alla Fresnel, si prendono in considerazione angoli ϑ piccoli, detta δ la distanza di P da P₀, valutata parallelamente a s, e f la distanza focale della lente, è ϑ≅δ/f; si trova così che il rapporto tra l’intensità I in P e quello, I₀, in P₀ vale

fig. 6

essendo λ la lunghezza d’onda della luce. Una relazione analoga, con s sostituito da t, si trova se ci si sposta da P₀ in direzione parallela alla dimensione t dell’apertura. Com’è evidente, per δ → 0, cioè per P → P₀, è I/I₀=1; si ha in tali condizioni un massimo assoluto per I; massimi relativi, di valore decrescente rapidamente al crescere di k, si hanno per δ=±(2k+1) λf/2s, mentre valori nulli si hanno per δ=±kλf/s, con k intero non nullo. L’aspetto della figura di d. che si ha in tale caso è mostrato nella fig. 6. La d. è dunque tanto più manifesta, e la figura di d. tanto più estesa, quanto più le dimensioni dell’apertura (s, t) sono piccole rispetto a λf; ammettendo che la figura di d. sfumi già per k dell’ordine della diecina, per f=1 m l’estensione della figura stessa risulta dell’ordine di 2 mm, 10 mm, 20 mm per s=5 mm, 1 mm, 0,5 mm, rispettivamente.

Analoghe, a parte l’introduzione di una simmetria circolare, sono le considerazioni che si svolgono nel caso di un’apertura circolare: le figure di d. sono simili a quelle che si ottengono nella d. alla Fresnel da fori circolari (fig. 2). Tale caso è molto importante nell’ottica strumentale: sono proprio queste le condizioni in cui si formano le immagini nel piano focale degli obiettivi dei telescopi, l’apertura diffrangente essendo costituita dall’obiettivo stesso, che raccoglie una minuscola porzione delle onde, sensibilmente piane, provenienti da sorgenti lontanissime. La teoria della d. nel caso degli strumenti ottici è principalmente dovuta a E. Abbe, il quale ha fra l’altro mostrato come sia appunto la d. a limitare il potere risolutivo degli strumenti.

2. D. di onde elastiche

Fenomeni di d. analoghi a quelli della luce si hanno anche nella propagazione di onde elastiche (per es., onde trasversali e longitudinali in mezzi solidi, onde superficiali nei liquidi, onde sonore nell’aria); grazie alla relativamente grande lunghezza d’onda, tali fenomeni sono in genere più cospicui e più facilmente osservabili rispetto a quelli della luce. Alla d. è dovuta, per es., sia la rotazione delle onde marine intorno alle opere di protezione dei porti (➔ onda), sia il contornare gli ostacoli da parte dei suoni, tanto più facilmente quanto più piccoli sono gli ostacoli e più gravi i suoni ecc.

3. D. di radiazioni corpuscolari

La d. delle radiazioni corpuscolari, prevista intorno al 1925 da L.-V. de Broglie, e dimostrata sperimentalmente per gli elettroni da C.J. Davisson e L.H. Germer nel 1927, costituisce una delle più brillanti conferme della meccanica ondulatoria. Tale fenomeno si verifica quando un fascio di particelle (elettroni, neutroni, protoni ecc.) attraversa un mezzo materiale o si riflette su di esso; in virtù delle interazioni con le particelle del mezzo, le particelle del fascio vengono deviate in modo da rarefarsi in certe direzioni e addensarsi in altre. Il fenomeno si presenta con particolare evidenza e regolarità nel caso che il mezzo sia cristallino, ed è allora governato, nel caso della d. da riflessione, dalla stessa legge che governa la d. dei raggi X, cioè dalla legge di Bragg (➔  Sir William Henry e William Lawrence Bragg): si svolge come se si avesse a che fare con radiazioni ondulatorie di lunghezza d’onda λ=h/p, essendo h la costante di Planck, e p la quantità di moto delle particelle in questione, in accordo con quanto stabilisce la meccanica ondulatoria.

4. D. dei raggi X

Fenomeni di d. si hanno nella propagazione dei raggi X in mezzi materiali: a diffrangere i raggi sono le molecole e gli atomi del mezzo, assimilabili a minuscoli ostacoli opachi le cui dimensioni (dell’ordine dell’Å) sono confrontabili con la lunghezza d’onda dei raggi.

5. D. di onde elettromagnetiche

È a causa della d. che le onde radio, specie quelle di relativamente grande lunghezza d’onda, contornano ostacoli anche molto estesi (rilievi montuosi, edifici ecc.) e pervengono in punti che vanno oltre l’orizzonte ottico dell’antenna trasmittente.