transizione

Passaggio da una condizione o situazione a una nuova e diversa

Biologia

In genetica, sostituzione, in una molecola di DNA, di una purina con un’altra purina o di una pirimidina con un’altra pirimidina; è uno dei meccanismi attraverso cui si possono verificare le mutazioni geniche di tipo puntiforme (➔ mutazione).

Chimica

Per gli elementi di t. ➔ elemento; per lo stato di t. ➔ cinetica.

Geografia

T. demografica

Espressione con la quale si indica la fase di aumento accelerato della popolazione interposta tra due fasi di sostanziale equilibrio: quella preindustriale, caratterizzata da natalità e mortalità elevate, e quella, tipica dei paesi industriali maturi, caratterizzata da notevole riduzione delle nascite e delle morti e tendenza alla crescita zero.

Fisica

Genericamente, il passaggio di un sistema da uno stato a un altro, di norma con scambio di energia con altri sistemi.

Radiazione di transizione

Quando una particella carica attraversa la superficie di separazione tra due mezzi con costante dielettrica diversa, oppure un dielettrico non omogeneo, per energie E tali che βγ≫1, essendo β=v/c il rapporto tra la velocità v della particella e quella c della luce nel vuoto e γ=E/m (con m massa a riposo della particella), si ha l’emissione di radiazione elettromagnetica di t., entro un cono in avanti di apertura ϑ∞1/γ e con spettro, che dipende dal prodotto βγ, nel campo dei raggi X.

T. di fase

Un sistema fisico subisce una t. di fase ogni volta che, al variare di alcuni parametri (come pressione, temperatura, intensità del campo magnetico, concentrazione di un componente ecc., detti parametri di controllo), alcune grandezze che caratterizzano il sistema (come entropia, capacità termica, resistenza elettrica, magnetizzazione ecc.) cambiano bruscamente, in modo discontinuo. Sono quindi t. di fase, per es., i cambiamenti di stato di aggregazione, il passaggio dallo stato di conduttore a quello di superconduttore o da conduttore a isolante, dallo stato ferromagnetico a quello paramagnetico ecc. Le t. di fase si possono classificare secondo il grado di discontinuità con cui le proprietà del sistema cambiano. Particolarmente avanzato è lo studio delle t. di fase in sistemi all’equilibrio termodinamico, le sole considerate nel seguito.

fig. 1

fig. 2

Classificazione delle t. di fase

Quando un sistema subisce una t. di fase al variare della temperatura T, trovandosi cioè per T<Tc nella fase F1 e per T>Tc nella fase F2, si possono distinguere due casi: a) t. di fase del prim’ordine, quando per passare dalla fase F1 alla fase F2 è necessario fornire al sistema una certa quantità di energia, detta calore latente di t., e quindi l’energia interna U del sistema è una funzione discontinua della temperatura (fig. 1); b) t. di fase di ordine superiore al primo, quando il calore latente è nullo e, quindi, l’energia interna è una funzione continua della temperatura. Si possono poi distinguere vari sottocasi. Se il calore specifico (cioè la derivata dell’energia interna rispetto alla temperatura) diverge o è discontinuo alla temperatura critica Tc (fig. 2), la t. è del second’ordine, altrimenti è di ordine superiore al secondo. In generale, se la derivata di ordine n dell’energia interna rispetto alla temperatura è continua, ma la derivata di ordine n+1 diverge o è discontinua, la t. è detta di ordine n+2. Nel caso in cui l’energia interna sia una funzione della temperatura infinitamente derivabile, ma non analitica nel punto T=Tc, la t. è di ordine infinito. Molto spesso questa classificazione viene semplificata: tutte le t. che non siano né del prim’ordine, né di ordine infinito, sono chiamate t. del second’ordine, dato che le t. di fase del second’ordine e quelle degli ordini successivi vengono studiate usando tecniche simili. Dal punto di vista sperimentale è difficile rilevare l’esistenza di t. di fase di ordine infinito, in quanto una funzione infinitamente derivabile si confonde facilmente con una funzione analitica. Le uniche informazioni su queste t., spesso presenti in materiali disordinati, vengono dalla teoria: il loro studio è molto complicato e i risultati ottenuti sono scarsi.

Se il parametro che controlla la t. non è la temperatura, la trattazione è molto simile: basta considerare l’energia libera A=U−TS, dove U è l’energia interna, T la temperatura termodinamica ed S l’entropia. In questo caso la derivata di A rispetto al parametro che controlla la t. ha un ruolo analogo all’energia interna nel caso precedente.

fig. 3

fig. 4

Diagramma delle fasi

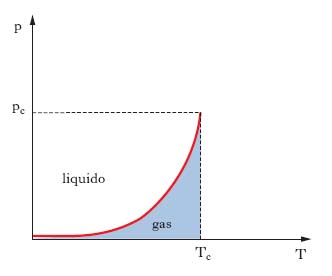
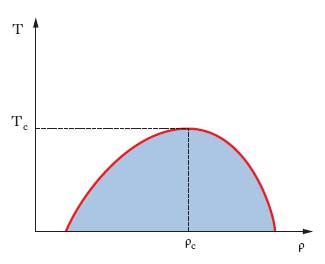
Può essere conveniente descrivere la struttura delle fasi mediante un diagramma bidimensionale detto diagramma delle fasi: in genere si riporta in ascissa la temperatura e in ordinata un parametro di controllo rilevante, per es., la pressione o il campo magnetico. Per ciascuna fase possibile del sistema viene indicata nel diagramma la regione corrispondente del parametro di controllo. Nella fig. 3 è riportato il diagramma delle fasi di una sostanza pura (per es., l’acqua) nel piano temperatura-pressione, per quanto riguarda la t. liquido-gas. La regione del diagramma occupata dalla fase fluida è connessa: la linea della t. gas-liquido termina, nel cosiddetto punto critico, ed è possibile passare dalla fase liquida alla fase gassosa senza incontrare una t. di fase, a patto di operare a pressioni e a temperature superiori a quelle del punto critico (200 bar e 400 °C per l’acqua ca.). Lo stesso diagramma delle fasi può essere rappresentato nel piano densità-temperatura (fig. 4). Nella zona in grigio chiaro il sistema si trova in una fase pura, ovvero spazialmente omogenea, nella zona in grigio scuro avviene una separazione delle fasi: per es., se la densità media del fluido è intermedia tra quella del gas e quella del liquido, parte del sistema sarà un gas e parte sarà un liquido. Il calore latente si annulla quando la pressione raggiunge il valore del punto critico, che è quindi un punto di t. del second’ordine. La linea delle t. gas-liquido è composta da t. di fase del prim’ordine e termina con una t. di fase del second’ordine: in moltissimi casi una t. di fase del second’ordine è il punto terminale di una linea di t. di fase del prim’ordine; i fenomeni che si osservano in vicinanza di un punto critico sono detti fenomeni critici.

T. di fase del prim’ordine e stati metastabili

Una delle caratteristiche delle t. di fase del prim’ordine è l’esistenza di stati metastabili: un sistema si trova in uno stato metastabile se può rimanere in questo stato per un periodo di tempo estremamente grande in assenza di perturbazioni esterne; tuttavia, a differenza di uno stato veramente stabile, una piccola, ma appropriata perturbazione, che può essere originata anche da una fluttuazione termodinamica, è sufficiente a provocare il passaggio dallo stato metastabile a uno stato più stabile. Un esempio è costituito dall’acqua soprafusa: l’acqua estremamente pura, se raffreddata lentamente, rimane liquida anche a temperature ben al di sotto di 0 °C. La presenza di qualsiasi impurità, o di granelli di ghiaccio, innesca un processo di cristallizzazione a catena. Lavorando con cura è possibile raggiungere temperature di −25 °C mantenendo l’acqua liquida. Lo stato metastabile inverso (ghiaccio surriscaldato) è estremamente difficile da ottenere, in quanto sulla superficie del ghiaccio c’è sempre un sottile strato di liquido che innesca il processo di fusione. Per quanto numerose siano le precauzioni prese, un pezzo di ghiaccio fonde, a partire dalla superficie, appena portato a una temperatura superiore a 0 °C.

T. ordine-disordine

Molto spesso è possibile caratterizzare una fase della materia mediante una proprietà di ordine o disordine. Per es., in un solido amorfo gli atomi sono disposti l’uno contro l’altro, in disordine; al contrario, in un cristallo, gli atomi sono ben ordinati e formano un reticolo regolare. Quando l’amorfo diventa un cristallo, gli atomi si dispongono in maniera più ordinata di prima: si ha quindi una t. da una fase disordinata a una fase ordinata, in breve una t. disordine-ordine. Il numero di reticoli regolari è estremamente elevato e a volte nella cristallizzazione di uno stesso sistema fisico gli atomi si dispongono secondo due diversi reticoli regolari. In questo caso si può avere una t. di fase in cui, al variare dei parametri fisici, si passa da una struttura ordinata a un’altra struttura ordinata. Secondo un modello molto semplice, un materiale ferromagnetico consiste di magnetini elementari (indicati per brevità come spin) che costituiscono la sorgente del campo magnetico e che possono essere orientati in varie direzioni (modello di Heisenberg). In un’ulteriore schematizzazione (che corrisponde a quello che in realtà accade in alcuni materiali) gli spin possono puntare in due sole direzioni, chiamate convenzionalmente alto e basso; l’interazione tra gli spin è tale da tendere a orientarli tutti nella stessa direzione (modello di Ising). Dato che l’agitazione termica ha un effetto opposto, tende cioè a disordinare gli spin, a bassa temperatura gli spin non sono disturbati dal rumore termico e riescono ad allinearsi gli uni con gli altri, mentre a temperatura più alta del punto di Curie non riescono a ordinarsi e puntano in varie direzioni. Nella fase paramagnetica ad alta temperatura il sistema è disordinato, mentre nella fase magnetica a bassa temperatura il sistema è ordinato.

Teoria delle t. di fase del prim’ordine

Il problema di determinare teoricamente per una data sostanza il diagramma delle fasi, sia nei suoi aspetti qualitativi, sia nei suoi aspetti quantitativi, se si esclude un numero estremamente ristretto di casi, concernenti alcuni sistemi bidimensionali, è risolvibile solo in maniera approssimata e per molti sistemi alcuni aspetti qualitativi non sono stati ancora ben compresi (per es., nella t. vetrosa, oppure liquido-amorfo). Si discute qui di seguito una delle approssimazioni più semplici, che rende ben conto del comportamento qualitativo e quantitativo delle più comuni t. di fase del prim’ordine. Il secondo principio della termodinamica implica che in un sistema a contatto con una sorgente a temperatura costante e che non compia lavoro, l’energia libera può solamente diminuire: quando l’energia libera assume il suo valore minimo, il sistema raggiunge l’equilibrio termodinamico. Il passo cruciale per determinare la struttura del diagramma delle fasi consiste nell’identificare uno o più parametri fisici che caratterizzino lo stato del sistema, e nel calcolare l’energia libera come funzione di questi parametri. I valori che i parametri assumono all’equilibrio vengono determinati cercando il minimo dell’energia libera. Nel caso dei sistemi magnetici il parametro più naturale è la magnetizzazione, mentre per la t. gas-liquido è la densità del fluido.

In un sistema magnetico di Ising, con magnetizzazione M proporzionale a un parametro d’ordine p, utilizzato per quantificare l’ordine presente in un sistema (nel caso di un materiale ferromagnetico è dato dalla percentuale di spin in alto meno la percentuale di spin in basso), nell’ipotesi che si possano trascurare le fluttuazioni del valore di tale parametro da punto a punto (ipotesi falsa vicino alle t. di fase del second’ordine), si ha la seguente condizione, necessaria ma non sufficiente, affinché l’energia libera sia minima: p=tgh[(Jp+h)/kT], dove tgh indica la tangente iperbolica, h è il campo magnetico espresso in unità opportune, J è una costante che dipende dal materiale ed è proporzionale all’accoppiamento tra i vari spin, k è la costante di Boltzmann. Calcoli abbastanza semplici mostrano che la temperatura di t. ferromagnetica, al di sotto della quale l’energia libera ha due minimi simmetrici per p diverso da zero, è data da Tc=k/J.

Nel caso della t. gas-liquido la densità ρ del fluido ha il ruolo del parametro d’ordine p; la trattazione più semplice di questa t. che risale a J.D. van der Waals, è sviluppata considerando una forza attrattiva fra le molecole, quando esse sono a grande distanza, per favorire energeticamente la fase liquida, e una forza repulsiva a corta distanza, per impedire alle molecole di sovrapporsi le une alle altre. Dopo aver fatto alcune semplificazioni sulla natura di queste forze e aver trascurato gli effetti delle fluttuazioni, si trova che la densità ρ soddisfa la seguente equazione: (P+aρ2)(ρ−1−b)=RT, dove P è la pressione, a e b sono due costanti dipendenti dal materiale (proporzionali rispettivamente alla forza attrattiva e alla forza repulsiva) e R è la costante dei gas. Utilizzando l’equazione precedente ed eliminando le regioni metastabili e instabili si trova un diagramma delle fasi abbastanza simile a quello delle fig. 3 e 4. Il punto critico, dove termina la linea di t. di fase del prim’ordine, è dato dai seguenti valori: Pc=a/27b2, ρc=1/(3b), Tc=8a/27Rb. I risultati che si possono ottenere mediante il metodo descritto sono in buon accordo con i dati sperimentali, se non si è troppo vicini al punto di t. di fase del second’ordine, nel qual caso la trattazione va modificata.

T. di fase del second’ordine

Il calore specifico di un sistema che subisce una t. del second’ordine, se calcolato con il metodo descritto sopra, risulta essere una funzione discontinua della temperatura; l’approssimazione principale consiste nel trascurare le fluttuazioni locali del parametro d’ordine, sia esso p o ρ, attorno al valore di equilibrio. Se si tiene conto perturbativamente di dette fluttuazioni, cioè se si fa l’ipotesi che il loro effetto sia piccolo, si trova per il calore specifico

C(T) = a ∣ T − T_c ∣^−a + b α = 1/2,

a e b essendo delle costanti dipendenti dal materiale, cioè esso diverge alla temperatura critica, mentre nell’approssimazione considerata precedentemente rimane finito. Non è quindi sostenibile l’ipotesi che l’effetto delle fluttuazioni rimanga piccolo vicino alla temperatura critica.

La teoria che permette di spiegare i fenomeni che avvengono vicino a una t. del second’ordine, detta teoria del gruppo di rinormalizzazione, è stata sviluppata, a cavallo fra gli anni 1960 e 1970, inizialmente da L.P. Kadanoff e successivamente da K.G. Wilson, il quale, per il suo contributo, ha ricevuto nel 1982 il premio Nobel. La difficoltà principale, nel trattare con metodi convenzionali le t. di fase di second’ordine, è dovuta (nel caso dei sistemi magnetici) al formarsi di regioni molto grandi nelle quali gli spin sono prevalentemente orientati nella stessa direzione. Un’analisi più precisa rivela che ciascuna regione si può decomporre in sottoregioni con le stesse caratteristiche: ognuna delle sottoregioni può a sua volta decomporsi in regioni ancora più piccole ecc.; la suddivisione si arresta quando il raggio della regione più piccola diventa uguale al passo reticolare. Il raggio della regione più grande (ξ) diverge alla temperatura critica. Il numero di gradi di libertà che giocano un ruolo importante tende all’infinito al punto di t. e il problema non è affrontabile direttamente con le approssimazioni usuali, in cui il numero di gradi di libertà deve rimanere finito. Il gruppo di rinormalizzazione fornisce uno strumento per aggirare questa difficoltà. Per semplicità si considera il caso della t. ferromagnetica nella schematizzazione del modello di Ising (l’estensione al caso generale non presenta difficoltà di principio), e si suppone che gli spin risiedano su un reticolo regolare cubico di passo a. Si può introdurre un reticolo di passo L (con L/a intero) sovrapposto al precedente; il parametro d’ordine locale relativo alla scala L (p_L) è definito sul nuovo reticolo ed è proporzionale alla somma di tutti gli spin in un cubo di lato L, la costante di proporzionalità essendo fissata dalla condizione ‹P_L2› = 1, dove il simbolo ‹ › denota il valore atteso su un opportuno insieme statistico. Per L=a, p_L coincide con il singolo spin e, per L che tende all’infinito, p_L è proporzionale all’usuale parametro d’ordine globale. La definizione di parametro d’ordine locale relativo alla scala L non è univoca; molte altre definizioni, fisicamente equivalenti, sono possibili. Nella fase di alta temperatura, p_∞ (ovvero p_L, per un valore di L molto grande rispetto al passo reticolare) è la somma di un numero infinito di variabili indipendenti e quindi, per il teorema del limite centrale, la sua distribuzione di probabilità è gaussiana; infatti, non essendoci magnetizzazione spontanea, gli spin che si trovano a distanza molto maggiore di ξ non sono praticamente correlati. Nella fase a bassa temperatura, p_∞ assume solo il valore 1 (oppure −1, a seconda del segno della magnetizzazione spontanea), in quanto non ci sono fluttuazioni attorno al valore medio della magnetizzazione (se esso è diverso da zero) su una regione macroscopica. Se per L abbastanza grande la distribuzione di probabilità delle variabili p_L è la stessa delle variabili p_2L, il sistema si dice invariante per trasformazioni di scala nella regione delle grandi distanze: la trasformazione che fa passare dalle variabili p_L alle variabili p_2L si chiama trasformazione di scala. Normalmente viene fatta l’ipotesi che il sistema sia sempre invariante per trasformazioni di scala: l’invarianza di scala del sistema anche al punto critico è una delle ipotesi che sta alla base del metodo del gruppo di rinormalizzazione. Si indichi con P_L la distribuzione di probabilità delle variabili p_L; dato che le variabili p_2L sono delle funzioni delle variabili p_L, la loro distribuzione di probabilità P_2L può essere calcolata a partire dalla distribuzione di probabilità P_L; in altri termini si ha

[1] P_2L = R(P_L),

dove R è un operatore non lineare che può essere più o meno complicato; la trasformazione [1] è una trasformazione di scala e l’operatore R è l’operatore di base del gruppo di rinormalizzazione; infatti gli operatori Rn, ottenuti applicando R n volte, formano un gruppo (o meglio un semigruppo) chiamato gruppo di rinormalizzazione. L’ipotesi di invarianza di scala implica che la distribuzione di probabilità per le variabili pL esista nel limite in cui L tende all’infinito; essa deve soddisfare l’equazione non lineare

[2] P_∞ = R(P_∞).

Si assume che tutte le informazioni relative al punto critico siano contenute nella P∞ da esso determinata e nelle proprietà di R nelle vicinanze di tale P∞. È quindi necessario determinare tutte le distribuzioni di probabilità possibili per le variabili pL per alti valori di L, cioè risolvere l’equazione [2]. In generale, le distribuzioni di probabilità di un sistema possono dipendere da un numero estremamente elevato di parametri e l’operatore R agisce su uno spazio con un numero infinito di parametri; si fa quindi l’ipotesi che sia possibile approssimare la vera distribuzione di probabilità P∞ con delle distribuzioni di probabilità relativamente semplici, che dipendono da un numero piccolo di parametri. Se si è in grado di valutare approssimativamente l’azione dell’operatore R su tali distribuzioni, si può trasformare la [2] in equazioni esplicite per un numero finito di variabili. L’idea alla base del procedimento esposto è che, se in un sistema fisico accadono fenomeni interessanti su scale diverse, ci saranno delle variabili che descrivono accuratamente quello che succede su una scala data, e quindi su ogni scala più grande, e delle equazioni che permettono di calcolare che valori assumono queste variabili, le leggi del moto. Nel caso considerato le variabili sono le pL mentre le leggi del moto sono le distribuzioni di probabilità PL. La teoria basata sul gruppo di rinormalizzazione concentra l’attenzione su come le leggi del moto cambiano quando si passa dalla descrizione su una scala a quella su un’altra scala. Da questo punto di vista il gruppo di rinormalizzazione ha una portata estremamente più vasta dello studio delle t. di fase del second’ordine.

Medicina

In istologia, epitelio di t., epitelio stratificato le cui cellule hanno accentuata plasticità e passano dalla forma piatta alla cilindrica, a seconda delle condizioni di maggiore o minore estensione della membrana epiteliale (per es., l’epitelio della vescica urinaria).

Tecnica

Nella tecnologia dei polimeri, la t. vetrosa è il passaggio di un materiale polimerico a struttura amorfa da uno stato vetroso, solido, fragile e tipico di un liquido sottoraffreddato (➔ sottoraffreddamento), a uno stato plastico, simile, al crescere della temperatura, a quello di un liquido ad alta viscosità; questa t. è legata alla modifica di natura e intensità delle interazioni fra macromolecole.

In metallurgia, la t. duttile-fragile è il fenomeno per cui nel raffreddamento degli acciai si ha notevole diminuzione di resilienza. Al di sopra di un dato intervallo di temperatura, tipico di ogni acciaio, si verifica una rottura di tipo tenace mentre al di sotto di esso si ha rottura di tipo fragile. La temperatura di t. a duttilità nulla è quella alla quale, in una t. duttile-fragile, si rompe l’acciaio sottoposto a prova di trazione che però non si rompe in una prova successiva a pari condizioni ma a temperatura superiore di 5,5 °C; tale temperatura, che si determina solo con prove ripetute, è per es. pari a −50 °C per un acciaio dolce incrudito.