mortalità

mortalità In demografia, il rapporto tra il numero di morti in un anno di osservazione e la popolazione da cui tali morti derivano.

Generalità

L’analisi degli aspetti quantitativi che si riferiscono alla morte degli uomini, sia prima della nascita (m. fetale), sia durante il corso della vita, costituisce un capitolo centrale nella demografia. La m. può essere esaminata come numero assoluto di morti, riferito alla popolazione complessiva (m. generica), oppure in senso specifico rispetto a segmenti della popolazione, come la m. per sesso, per stato civile, per titolo di studio, per tipo di attività svolta, e così di seguito. In conseguenza delle modificazioni che l’uomo ha introdotto nel proprio ambiente e nonostante alcune di esse agiscano in senso negativo, la m. generica risulta generalmente decrescente nel tempo; tale diminuzione si è accentuata nel 19° e nel 20° sec. e si registra, sia pure con ritmi diversi e con partenze temporali differenti, in tutti i paesi. Questo ha fatto ritenere che lo sviluppo di una popolazione umana risponda a una legge e che si passi da una fase di elevata natalità e m. a una fase di bassa natalità e bassa m. attraverso un periodo di transizione, da cui appunto il nome di transizione demografica

La m. specifica per età viene calcolata quando è possibile classificare i decessi secondo l’età dei deceduti e la popolazione di origine, anch’essa divisa per le stesse età o classi di età. Si tratta della più importante e più usata specificazione nello studio della mortalità. La distribuzione per età dei decessi in un determinato paese, in un certo periodo di osservazione, presenta un andamento caratteristico plurimodale con due o tre massimi: un primo massimo molto elevato si presenta al primo anno di vita; un secondo massimo, generalmente assoluto, si verifica nelle età più anziane, in maniera variabile da popolazione a popolazione; un terzo massimo, meno evidente, si verifica attorno ai 20 anni. La curva che rappresenta la distribuzione per età dei decessi prende il nome dal demografo W. Lexis; la ripartizione dei casi attorno al valore modale dell’età anziana avviene in maniera pressoché paritaria fra i casi prima e quelli dopo tale età: una certa popolazione, in un certo periodo storico, vivrebbe tutta fino all’età modale, il punto di Lexis; vi sono però individui che vengono decimati dalla morte prima di tale traguardo e altri dopo, in maniera casuale, così come avviene per la distribuzione gaussiana degli errori accidentali. Le morti infantili e quelle a 20 anni sarebbero, invece, motivate da fattori ambientali.

Nell’ambito della m. differenziale spicca il fenomeno della supermortalità maschile: in ogni età la m. specifica è superiore per i maschi rispetto alle femmine (per cause genetiche, ambientali, fisiologiche); a questa si aggiungono altre variabili demografico-sociali: per es. la m. dei celibi o dei vedovi è più elevata di quella dei coniugati e quanto più elevato è il livello sociale di un individuo, tanto più bassa risulta la mortalità.

Le condizioni ambientali e il livello socioeconomico raggiunto differenziano la m. per causa: malattie infettive, avitaminosi, dissenteria, denutrizione costituiscono le motivazioni della decimazione di vasta parte di popolazioni in via di sviluppo mentre nelle società industrializzate sono le malattie ‘moderne’ (patologie dell’apparato cardio-circolatorio e tumori) derivanti da stress e da condizioni ambientali a rischio ecologico a causare il maggior numero di morti.

M. infantile

La m. infantile costituisce un aspetto molto importante della m. di una popolazione e rappresenta uno degli indicatori demografici più rilevanti per significare il livello socioeconomico di un paese. Essa viene misurata come rapporto fra il numero dei morti entro il primo anno di vita e il numero di nati vivi da cui tali morti derivano, con riferimento a un anno di calendario, per un determinato territorio e, ove possibile, secondo alcune caratteristiche (per sesso, per causa di morte, per durata di vita nell’arco del primo anno di sopravvivenza, e così via). Le cause della m. infantile possono essere endogene, quelle legate alla gravidanza, siano esse di carattere genetico o di carattere patologico (traumi alla donna, alcolismo, traumi fetali), ed esogene, quelle legate all’ambiente esterno e alle condizioni di vita (allattamento, incidenti dovuti a disattenzione, scarsa igiene e profilassi, denutrizione). La m. infantile è diminuita dovunque, tanto che si definisce la categoria dei paesi ad alta m. infantile adottando come limite inferiore il 40‰.

Tavole di mortalità

Le tavole di m. costituiscono un caso specifico delle più generiche tavole di eliminazione, in cui si determinano le diverse probabilità di estinzione di una generazione o di una coorte di eventi (per es., di matrimoni) secondo determinate modalità. Nelle tavole di m. si considera una generazione fittizia di 100.000 nati che vengono progressivamente eliminati per morte nelle varie età fino all’età ω che convenzionalmente costituisce l’età estrema non raggiunta da nessun componente della generazione (in quanto l’ultimo individuo del gruppo muore tra il compleanno x-1 e il compleanno x). La difficoltà nella costruzione delle tavole è relativa al calcolo delle probabilità di morte tra il compleanno x e il compleanno x+1. Tali probabilità si determinano facendo il rapporto tra i casi favorevoli (decessi in età fra x e x+1) e i casi possibili (esposti al rischio di morte, pari ai sopravviventi al compleanno x). Le tavole di m. si presentano come un prospetto in cui figurano, in corrispondenza delle varie età (poco più di un centinaio di anni), il numero dei decessi d_x, il numero dei sopravviventi residui l_x, le probabilità di morte q_x, per ciascuna età. Queste tre grandezze sono legate logicamente tra di loro dalla relazione q_x=d_x/l_x.

La tavola di m. comprende altre ‘funzioni biometriche’, costituite da: probabilità di sopravvivenza, che è complementare alla probabilità di morte (p_x=1−q_x); la serie cumulata degli anni vissuti N; la serie retrocumulata degli anni vissuti T; la vita media o speranza di vita e_x; e la vita probabile o età mediana alla morte π_x. Se definiamo con anni vissuti l’intervallo temporale compreso tra l’età x e l’età x+1 in cui un soggetto muore, che per semplicità attribuiamo al valore centrale della classe di età (L_x=(l_x+l_x+1)/2), ogni individuo si caratterizza per un proprio valore di L_x. Così alcuni moriranno tra 0 ed 1 anno (in media, mezzo anno di vita), altri moriranno tra 1 e 2 anni (in media 1,5 anni vissuti), altri tra 2 e 3 anni (in media 2,5 anni vissuti) ecc. Sommando tutti gli anni di vita vissuti dai singoli componenti della generazione e dividendo questo ammontare per il numero totale dei componenti (nel caso delle tavole italiane è generalmente 100.000), si ottiene la vita media ovverosia il numero di anni vissuti in media dagli elementi della generazione. La vita probabile è invece rappresentata dal numero degli anni che occorrono affinché il contingente dei sopravviventi all’età x si dimezzi. Fra i due indicatori, sicuramente più utilizzato è il primo.

figura

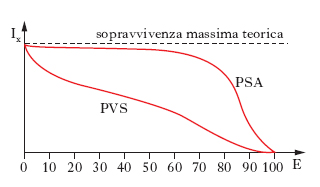
Quando occorre fare confronti fra situazioni (temporali o territoriali) diverse, per rappresentare il livello di m. si fa ricorso alla vita media alla nascita. In figura sono disegnate le curve dei sopravviventi nel caso di due popolazioni: la prima appartenente al gruppo dei paesi a sviluppo avanzato (PSA), la seconda a quello dei paesi in via di sviluppo (PVS). Nell’ipotesi che tutta la generazione raggiungesse l’età (E) di 100 anni, la curva sarebbe rettangolare in quanto i sopravviventi (l_x) sarebbero, teoricamente, sempre pari al contingente iniziale; solamente al raggiungimento del centesimo anno morirebbero tutti. La realtà è diversa e la curva sarà tanto più bassa quanto più accanita è la m. nelle varie età. La curva di un paese a sviluppo avanzato risulta tendenzialmente vicina alla curva teorica di massima sopravvivenza; la curva di un paese in via di sviluppo, notevolmente più bassa. L’area compresa tra le due curve rappresenta il totale degli anni vissuti che il paese in via di sviluppo perde, in confronto con un paese a sviluppo avanzato, per effetto della mortalità. La stima delle probabilità di morte contenute in una tavola di m. si effettua sulla base dei tassi di m. che vengono calcolati sui ‘contemporanei’. È evidente che per calcolare le probabilità di morte di una generazione di nati in un certo anno si dovrebbe attendere la completa estinzione della generazione stessa, cioè circa 100 anni: si ricorre allora a una generazione fittizia in cui il modello della m. è quello che viene registrato dalle statistiche dei decessi in un dato anno di calendario.

Si definiscono tavole di m. ridotte quelle in cui le età vengono raggruppate in classi (generalmente quinquennali o decennali). Per tenere conto che in moltissimi paesi in via di sviluppo le registrazioni anagrafiche sono deficitarie e che quindi è impossibile stabilire le proprie tavole di m., sono state elaborate alcune tavole-tipo; l’accesso per la utilizzazione è costituito da alcune ‘chiavi’ come la dislocazione geografica del paese, i livelli di m. infantile, la speranza di vita a 10 anni. Le tavole di m. trovano ricorrente impiego nel settore assicurativo e nelle previsioni demografiche.