diagramma

Botanica

Proiezione grafica schematica orizzontale dei tratti d’inserzione di fillomi (foglie, brattee, parti del fiore) su un asse (fusto, asse fiorale) immaginato di forma conica. Nel d. il centro corrisponde all’apice dell’asse, ogni nodo o piano d’inserzione è rappresentato da un cerchio e perciò si hanno parecchi cerchi concentrici. Se i fillomi sono isolati, su ogni cerchio vi è un solo segno (un grosso punto, una linea ad arco o un cerchietto), se i fillomi sono verticillati, su ogni cerchio si hanno due o più segni; nel primo caso, eventualmente, i segni sono riuniti da una linea spirale. Nei d. fiorali un punto segnato al disopra del d. indica l’asse dal quale nasce il fiore, una linea ad arco segnata al disotto indica la brattea ascellante (quando esistono, si possono indicare anche le bratteole). I d. sono utili per mettere in evidenza le varie fillotassi, per chiarire la disposizione degli assi successivi nelle infiorescenze, e particolarmente per indicare il numero e i rapporti di posizione, aderenza, sviluppo, e di simmetria delle diverse parti fiorali; ciò facilita il confronto, spesso necessario nella sistematica, dei generi di una famiglia o di famiglie diverse.

Chimica

D. di stato Costruzioni grafiche che riportano i valori delle variabili (temperatura, pressione, composizione) coinvolte nella caratterizzazione delle fasi di un sistema termodinamico a uno o più componenti. Forniscono, pertanto, la rappresentazione grafica del campo di esistenza delle fasi coesistenti in condizioni di equilibrio e della loro composizione. Nella maggior parte dei casi vengono ricavati sperimentalmente; la regola delle fasi e la legge di Gibbs-Duhem interpretano e verificano la correttezza dei dati raccolti. Tuttavia, è possibile ricavare i campi di stabilità delle diverse fasi anche partendo dalla conoscenza delle proprietà termodinamiche del sistema quali l’energia libera della miscela che in condizioni di equilibrio, a temperatura e pressione costanti, assume un valore estremo, minimo se l’equilibrio è stabile. Lo sviluppo dei calcolatori ha agevolato la costruzione dei d. di stato tanto da favorire l’affermazione di un particolare settore di ricerca che viene indicato con l’acronimo CALFAD (calculation of phase diagrams).

fig. 1

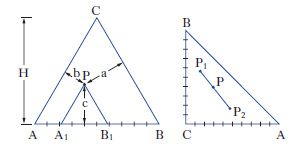
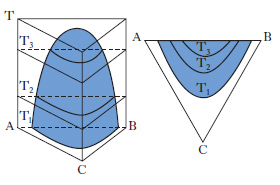
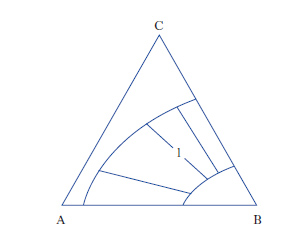
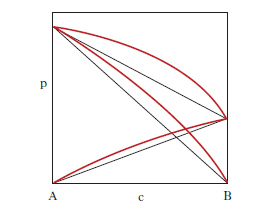
Per sistemi a un componente sono sufficienti d. che adottano, come coordinate, la pressione e la temperatura. Per i sistemi binari a due componenti, la composizione è riportata su un segmento rettilineo orizzontale, i cui estremi sono rappresentativi dei componenti puri, mentre sui punti interni si legge la composizione delle fasi presenti e quella complessiva del sistema. Sull’ordinata viene riportata la temperatura (considerando costante la pressione: diagrammi isobari) o la pressione (considerando costante la temperatura: diagrammi isotermi). Per sistemi ternari, la composizione viene rappresentata su un diagramma triangolare, solitamente equilatero (fig. 1). I tre vertici rappresentano i componenti puri A, B, C, mentre i punti su ciascun lato danno le composizioni delle miscele binarie AB, AC, BC. I punti interni al triangolo rappresentano tutte la composizione delle miscele ternarie ABC. In particolare da un punto interno P si tracciano le parallele ai lati AC e BC fino a intersecare il lato AB nei punti A₁ e B_1, per cui risulta A%=100∙B₁B/AB, B%=100∙AA₁/AB; C%=100∙A₁B₁/AB. Alternativamente da P si conducono le perpendicolari ai lati, individuando così i tre segmenti a, b, c; risulta: A%=100∙a/H, B%=100∙b/H, C%=100∙c/H, essendo H l’altezza del triangolo.

Equilibri solido-liquido

fig. 2 A

fig. 3

fig. 4

fig. 5

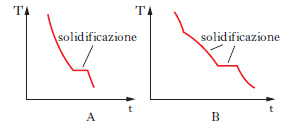
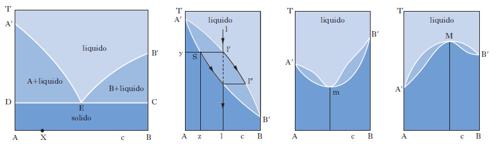
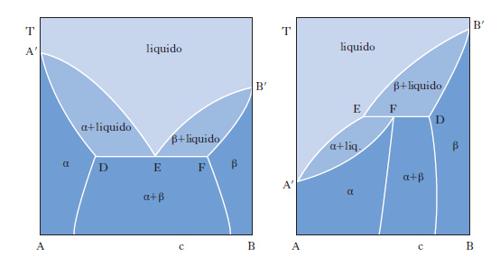
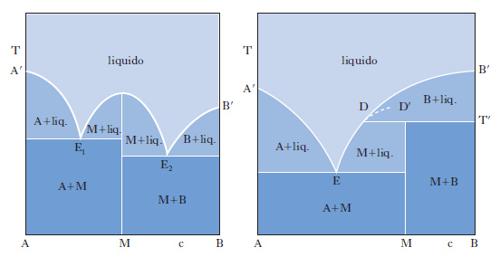
Il metodo sperimentale comunemente impiegato per ottenere i dati degli equilibri solido-liquido è quello dell’analisi termica, che consiste nel rilevare le curve di raffreddamento o di riscaldamento (curve tempo-temperatura) di sostanze pure e di loro miscele. Se si lascia raffreddare un metallo puro fuso e si misura la sua temperatura a intervalli regolari di tempo si osserva che, finché il metallo è allo stato liquido, la curva di raffreddamento si svolge con andamento regolare (in genere esponenziale), ma quando inizia la solidificazione la temperatura resta costante finché il fenomeno non è terminato (fig. 2 A). Quindi la temperatura diminuisce regolarmente con una legge dello stesso tipo di quella seguita dal liquido e la curva di raffreddamento non presenta altre anomalie, a meno che il metallo non possa esistere allo stato solido in più forme allotropiche. Se si lascia raffreddare una lega fusa di due metalli miscibili allo stato liquido ma immiscibili in quello solido, raggiunta una certa temperatura si osserva la comparsa di una fase solida costituita da uno dei due metalli; a questo punto la curva di raffreddamento mostra un brusco cambio di pendenza e la temperatura continua a diminuire. La deposizione di questa fase continua finché, a una temperatura più bassa, si ha la separazione contemporanea dei due metalli (fig. 2 B), che prosegue fino alla completa solidificazione del campione, senza variazioni di temperatura (temperatura eutettica). Con riferimento ai sistemi a due componenti si possono distinguere i quattro casi illustrati nella fig. 3. Il primo si riferisce al caso di componenti completamente immiscibili allo stato solido, il secondo a componenti completamente miscibili allo stato liquido e solido, mentre il terzo e il quarto a componenti miscibili con un minimo della temperatura di fusione (Cu-Mn, Cu-Au, As-Sb) e con un massimo (situazione rara che si riscontra nelle forme d ed l di un composto otticamente attivo). Le curve nella fig. 4 si riferiscono a componenti parzialmente miscibili allo stato solido: la prima presenta un punto eutettico in corrispondenza del quale la temperatura di fusione della miscela è inferiore a quella dei componenti puri. Infine le curve nella fig. 5 si riferiscono rispettivamente a miscele che formano composti con un punto di fusione congruente o incongruente poiché si decompone prima di fondere.

Equilibri liquido-liquido

fig. 6

fig. 7

fig. 8

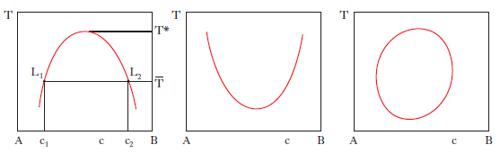
Si riferiscono a miscele di liquidi i cui componenti, presentano lacune di miscibilità. La loro conoscenza è alla base delle operazioni di estrazione con solvente. L’influenza della pressione sugli equilibri liquido-liquido è così modesta che in generale può essere ignorata: pertanto nei d. di stato compaiono come variabili soltanto la composizione delle fasi e la temperatura. Nel caso di sistemi a due componenti la curva di miscibilità può presentare una temperatura critica di soluzione superiore (per es., acqua-fenolo, acqua e n-butanolo; fig. 6, a sinistra), inferiore (per es., acqua-dietilammina, acqua e 4-metilpiperidina; fig. 6, al centro) o sia inferiore sia superiore (per es., acqua-nicotina, acqua-metiletilchetone; fig. 6, a destra). Riferendoci, come esempio, al primo caso della fig. 6, si osserva che in corrispondenza a temperature superiori a T*, i due liquidi sono completamente miscibili; se la temperatura è inferiore a T*, esiste un intervallo di concentrazione in cui il sistema si separa in due miscele fra loro in equilibrio (lacuna di miscibilità): per es., alla temperatura T‾ ogni sistema il cui punto rappresentativo cade all’interno del segmento L₁^‒‒L₂^- si smiscela in due miscele che sono rappresentate dai punti L₁ e L₂, con composizione rispettivamente c₁ e c₂; con la regola della leva si calcola il rapporto fra le quantità di L₁ e L₂. Se invece il punto rappresentativo cade all’esterno del segmento L₁^‒‒L₂^-, la miscela resta omogenea in quanto per concentrazioni minori di c₁ e maggiori di c₂ i due componenti del sistema sono completamente miscibili fra loro; come risulta dal primo caso in fig. 6, i valori c₁ e c₂ dipendono dalla temperatura. Nel caso di sistemi a 3 componenti, gli equilibri liquido-liquido sono rappresentati graficamente da prismi retti a base triangolare (fig. 7, a sinistra), che possono essere ricondotti a figure bidimensionali proiettando sul triangolo delle composizioni le isoterme corrispondenti alle diverse temperature (fig. 7, a destra). La fig. 7, a destra, prende in esame un equilibrio ternario in cui delle tre coppie binarie possibili, AB, AC, BC, soltanto una, AB, presenta miscibilità parziale, mentre nelle altre due coppie i componenti sono completamente miscibili in tutti i rapporti. Le coppie binarie con miscibilità parziale possono anche essere due (fig. 8) dove l sono le linee coniugate, cioè le linee che collegano i punti rappresentativi di due miscele liquide in equilibrio.

Equilibri liquido-vapore

fig. 9

fig. 10

fig. 11

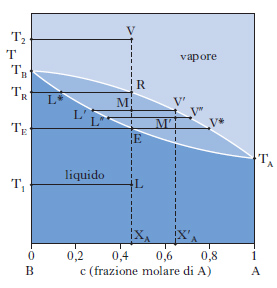
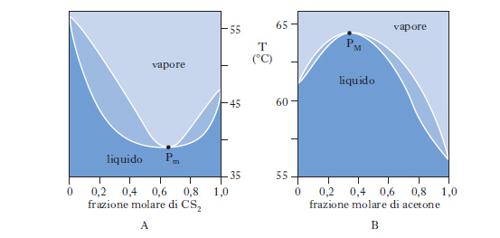
Sono alla base delle operazioni di distillazione. Se ci riferiamo a due liquidi totalmente miscibili e la miscela, comportandosi idealmente, obbedisce alla legge di Raoult per tutto l’intervallo di concentrazione riportando in ordinate la tensione di vapore di ciascun componente a una data temperatura e in ascisse la corrispondente percentuale molare nel liquido, si ottengono due rette passanti per l’origine. La maggior parte delle miscele liquide presenta deviazioni positive dal comportamento ideale (linee nere di fig. 9) per cui la tensione di vapore p misurata risulta maggiore di quella prevista per le miscele ideali. Se tra le molecole dei due componenti si manifestano intense forze di attrazione, si osservano deviazioni negative dal comportamento ideale e la curva di tensione di vapore misurata risulta inferiore a quella della miscela ideale. Per i processi di distillazione interessa conoscere oltre all’andamento dei punti di ebollizione in funzione della composizione della miscela, anche la composizione del vapore in equilibrio con il liquido bollente (andamento dei punti di rugiada). Nella fig. 10 è riportata la tipica forma lenticolare di un d. di stato liquido-vapore: la curva inferiore, luogo dei punti di ebollizione di tutte le possibili miscele dei due componenti A e B, e la curva superiore, luogo dei punti di rugiada, si congiungono in corrispondenza dei punti di ebollizione, T_A e T_B, dei due componenti puri. La composizione è tradizionalmente definita in termini di frazione molare x del componente più volatile (A nella fig. 10, in cui è T_A〈T_B). La zona del d. superiore alla curva dei punti di rugiada corrisponde alla zona di esistenza della sola fase vapore; l’area compresa fra l’asse delle ascisse e la curva di ebollizione è caratteristica del solo stato liquido; nell’area fra le due curve coesistono in equilibrio entrambe le fasi. Sempre con riferimento alla fig. 10, si consideri una miscela, di composizione x_A e alla temperatura T₁, il cui punto rappresentativo, L, cade nella zona di esistenza della sola fase liquida; si voglia riscaldare la miscela fino alla temperatura T₂, a cui corrisponde un punto rappresentativo, V, nella zona di esistenza della sola fase vapore. Durante il riscaldamento, la soluzione si mantiene completamente allo stato liquido fino alla temperatura T_E (punto E), alla quale cominciano a svolgersi i primi vapori: T_E è la temperatura di ebollizione della miscela di composizione x_A. Aumentando ancora la temperatura, si entra nella zona di coesistenza delle due fasi. Nel punto M la miscela originale si è separata in una fase vapore V′ e in una fase liquida L′ e il rapporto fra la quantità di vapore v e la quantità di liquido l si determina in base alla regola della leva: v/l=ML′/MV′. Naturalmente, la somma di v e l è pari alla quantità di soluzione liquida inizialmente presa in esame. Sono essenziali le considerazioni seguenti: a) nel campo di coesistenza delle due fasi, il vapore, rispetto al liquido in equilibrio, è più ricco nel componente più volatile; b) il rapporto fra l e v va man mano diminuendo al crescere della temperatura, finché in corrispondenza a T_R, temperatura di rugiada, la fase liquida scompare; c) fra T_E e T_R i punti rappresentativi della fase vapore sono compresi nel tratto di curva fra V* e R, mentre la fase liquida in equilibrio è rappresentata dai punti del tratto di curva fra E e L*; d) la fase vapore risulta tanto meno arricchita nel componente più volatile quanto maggiore è il rapporto v/l. Per temperature superiori a T_R, si entra nel campo di esistenza della sola fase vapore, a cui appartiene il punto V rappresentativo della miscela alla temperatura finale T₂. Per ottenere una separazione della miscela occorre, pertanto, interrompere il riscaldamento nel campo di temperature compreso fra T_E e T_R, per es. nel punto M, dove il vapore V′ si trova al punto di rugiada corrispondente a una miscela di frazione molare X′_A (>X_A). Separando le fasi e condensando parzialmente la miscela V′ fino al punto M′, accanto al liquido L′ viene a coesistere un nuovo vapore V′, ancor più arricchito nel componente più volatile. Per successive separazioni e condensazioni parziali, si può pervenire al componente A praticamente puro. In modo del tutto analogo, L′ può essere parzialmente evaporato e, procedendo per successive separazioni ed evaporazioni parziali, come succede in una distillazione, si può pervenire al componente B praticamente puro. Nella fig. 10 le temperature di ebollizione di tutte le possibili miscele di A e di B sono intermedie rispetto a quelle dei componenti puri; questo comportamento trova, però, numerose eccezioni: esistono miscele binarie, la cui curva di ebollizione presenta un minimo, come il sistema solfuro di carbonio-acetone, o un massimo, come il sistema acetone-cloroformio (fig. 11): ciò può accadere quando le deviazioni positive o negative fra tensione di vapore misurata e tensione di vapore calcolata in base alla legge di Raoult risultano molto forti. Nei punti di minimo, o di massimo, detti punti azeotropici, le curve di ebollizione e di rugiada sono tangenti: la miscela la cui composizione corrisponde a tali punti, detta miscela azeotropica, evapora completamente a temperatura costante e non in un intervallo di temperatura, come avviene per le miscele di diversa composizione. Se il d. di equilibrio presenta punti azeotropici, la distillazione, comunque condotta, non può mai separare entrambi i componenti allo stato puro.

fig. 12

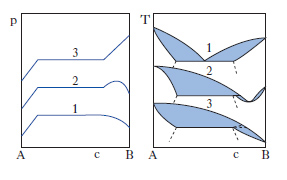
Per liquidi parzialmente miscibili le curve composizione-tensione di vapore totale in corrispondenza di una isoterma passante per la lacuna di miscibilità possono essere di tre tipi (fig. 12, a sinistra), tutti relativi a deviazioni positive dalla legge di Raoult. In ogni curva si distinguono tre tratti: nel primo e nel terzo la tensione di vapore varia con la composizione e il sistema è costituito da una sola fase liquida; nel secondo invece la tensione di vapore è indipendente dalla composizione: tale tratto corrisponde all’intervallo di concentrazione della lacuna di miscibilità. I tre d. temperatura-composizione corrispondenti ai tre tipi di curve sono riportati nella fig. 12, a destra. In ogni caso la curva superiore è quella del vapore e la curva inferiore è quella del liquido.

Per liquidi totalmente immiscibili la tensione di vapore è eguale alla somma di quelle dei singoli componenti. Pertanto, essendo la tensione totale indipendente dalla quantità relativa dei due componenti, il sistema bolle a temperatura costante finché sono presenti i due strati liquidi.

Informatica

Grafo orientato, utilizzato in particolare per la rappresentazione dell’evoluzione temporale di sistemi (automi, algoritmi, sorgenti di informazione ecc.). Per il d. di flusso ➔ flowchart.

Matematica

fig. 13A

fig. 14

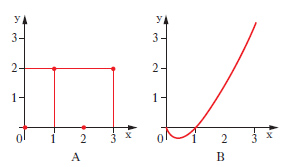
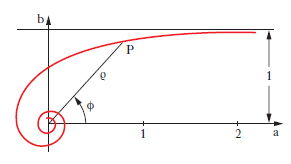
D. piano Rappresentazione grafica, piana, di una qualsiasi grandezza dipendente soltanto da un’altra, cioè di una funzione di una sola variabile. Tale rappresentazione raffigura l’andamento di una funzione con molto maggiore evidenza che una semplice tabulazione. Anche una funzione di due variabili si può rappresentare graficamente, nello spazio, mediante un opportuno d. (che prende allora il nome più proprio di stereogramma) oppure nel piano mediante una famiglia di d. (che prende allora il nome di nomogramma) o, più semplicemente, mediante le sue curve di livello. I d. piani sono di solito di tipo cartesiano o di tipo polare (➔ anche coordinate). Il d. cartesiano di una funzione y=f(x) si costruisce segnando su un piano cartesiano xy i punti di coordinate (x, f(x)) per diversi valori di x nel dominio di f. Una funzione può essere determinata da una legge di tipo matematico, che per lo più si concreta in una formula, o viceversa può avere carattere empirico. Sia in un caso sia nell’altro può non aver senso congiungere quei punti con una linea: i punti già di per sé costituiscono il d. della funzione che viene detto d. a punti o a ordinate. Per es., il d. della funzione che assume il valore 2 in corrispondenza a valori dispari della x e il valore zero per ogni altro valore intero si presenta come in fig. 13A. Viceversa, quando il d. è una curva nel senso intuitivo della parola, si parla senz’altro, con linguaggio piuttosto improprio ma di uso corrente, di ‘curva’ di un dato fenomeno, di una data funzione ecc.: in fig. 13B, per es., è indicata la curva della funzione y=x log x. Nei d. di funzioni empiriche va tenuto conto degli eventuali errori da cui è affetta ciascuna misurazione. Quando la cosa abbia senso nulla vieta di congiungere i vari punti ottenuti mediante segmenti rettilinei (prima approssimazione) o, con le opportune cautele, mediante una curva. Nei d. polari la posizione di ciascun punto, P, viene definita mediante la sua distanza (raggio vettore, ρ) da un punto fisso del piano (polo) e mediante l’ampiezza dell’angolo (anomalia, ϕ) che il raggio uscente dal polo e passante per il punto forma con un raggio fisso (asse polare, a), pure uscente dal polo. I valori, positivi o negativi, della variabile indipendente si assumono come anomalie, riportandoli nel senso di rotazione che sarà quello assunto come positivo (generalmente il senso antiorario) se positivi, in quello contrario se negativi; i valori della funzione si assumono come raggi vettori. In fig. 14 è riportato il d. polare della funzione ϱ=1/ϕ. Si tratta di una curva che compie infiniti giri attorno al polo, che è un suo punto asintotico: in fig. è rappresentata solo metà della curva, in relazione ai valori positivi di ϕ (l’altra metà è simmetrica di quella indicata rispetto alla retta b).

Nella statistica e nell’economia si usano spesso d. di tipo polare per rappresentare fenomeni che si svolgono nel tempo: rispetto ai d. cartesiani si ha allora il vantaggio di poter paragonare in modo immediato i valori della grandezza in esame all’inizio e al termine dell’intervallo di tempo che si considera.

Linguistica

fig. 15

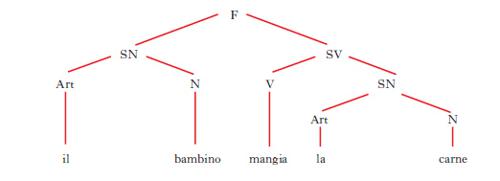
D. ad albero (o anche, semplicemente, albero) Rappresentazione grafica della struttura in costituenti di una frase (fig. 15). Le linee che collegano i vari simboli si chiamano rami; ogni punto di ramificazione segnato con un simbolo prende il nome di nodo. La cima dell’albero è indicata con il simbolo F (=frase); da qui si dipartono due rami terminanti con i simboli SN (=sintagma nominale) e SV (= sintagma verbale), che rappresentano i costituenti immediati della frase; dai simboli SN e SV si irradiano altri rami terminanti con altri simboli (N = nome, V = verbo, Art = articolo ecc.), i quali designano i diversi costituenti dei sintagmi; le linee verticali stanno a indicare la sostituzione dei simboli con parole della lingua.

Tecnica

fig 16

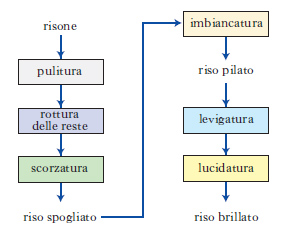
D. a blocchi Schema grafico della sequenza di operazioni da compiere, per es., in un processo industriale, in cui ciascuna operazione è indicata o scritta in un riquadro (detto, appunto, blocco; fig 16), e la loro successione è indicata con frecce.

D. fiume Schema grafico in cui l’entità dei flussi (di materiali, di energia ecc.) nelle sezioni caratteristiche di un impianto industriale è direttamente proporzionale agli spessori delle strisce rappresentative dei flussi stessi.