nodo

Anatomia

N. del seno (o n. seno-atriale) Formazione anatomica situata nell’atrio destro del cuore, in corrispondenza dello sbocco della vena cava superiore, importante nella regolazione del ritmo cardiaco.

Astronomia

Per un pianeta, e anche per la Luna e altri astri planetari, n. sono i due punti in cui l’orbita taglia l’eclittica. N. dell’eclittica (o punti equinoziali o equinozi) sono i due punti in cui questa taglia l’equatore celeste. Linea dei n. è la retta congiungente i due n., intersezione del piano dell’orbita del corpo celeste considerato con il piano dell’eclittica.

Biologia

In embriologia, n. embrionale, gruppo di cellule della blastocisti, da cui si origina l’embrione nei Mammiferi; n. cefalico (o n. di Hensen), gruppo di cellule situato all’estremità cefalica della linea primitiva nell’embrione degli Uccelli e dei Mammiferi.

Botanica

Punto di inserzione delle foglie sul fusto. Anatomicamente, la struttura del fusto in corrispondenza del n. è diversa da quella degli internodi, anche perché vi permangono a lungo gruppi di cellule meristematiche che consentono l’accrescimento intercalare. La struttura nodulare che si forma per inclusione di rami, vivi o morti, nel tronco durante il suo accrescimento diametrico è detta n. del legno; esso si evidenzia nelle sezioni del legname lavorato.

Il fusto che presenta un vistoso ingrossamento nei n. si chiama fusto nodoso (es. garofano), mentre la radice nodosa è quella che ha tratti tuberosi intercalati a porzioni sottili.

Geografia

In geografia fisica, n. orografico, la zona dove si incontrano due o più serie di rilievi montuosi aventi direzione diversa, e che costituisce in genere anche un n. idrografico, convergendovi le linee displuviali di vari bacini contermini.

Matematica

Punto doppio di una curva piana, nel quale le tangenti principali sono reali e distinte. In senso più esteso, è un punto origine di due rami lineari, cioè, in forma intuitiva, un punto per il quale la curva passa due volte. Il termine si applica anche alle linee sghembe, con lo stesso significato, e si estende alle superfici, per indicare un punto doppio conico ovvero biplanare; in una superficie si può presentare anche una linea tutta costituita da n.: essa si dice linea (doppia) nodale (➔ nodale).

Tipi di nodi

fig. 1

Per le curve piane soddisfacenti a opportune ipotesi di regolarità, in particolare per le curve algebriche piane, i n. si distinguono in vari tipi, a seconda del comportamento della curva in un intorno del n. stesso: n. ordinario (fig. 1): ciascuna delle tangenti principali ha, con la curva, nel punto P, molteplicità d’intersezione eguale a 3; flecnodo, o biflecnodo a seconda che nel punto d’intersezione i due rami della curva presentino rispettivamente uno o due flessi, oppure tacnodo se hanno la stessa tangente e oscnodo lo stesso cerchio osculatore.

Dal punto di vista analitico un n. si riconosce come segue: ammesso che il punto P considerato abbia coordinate (a, b), rispetto a un prefissato riferimento cartesiano, scelto in modo che l’asse y non sia parallelo alle tangenti principali, nell’intorno di P la curva si può approssimare quanto si vuole con due curve paraboliche. Le due serie di potenze che rappresentano i due rami della curva uscenti da P, sono

y=b+c₁ (x−a)+c₂ (x−a)²+… ,

y=b+c′₁ (x−a)+c′₂ (x−a)²+…;

e le tangenti principali sono allora le rette

y=b+c₁ (x−a); y=b+c′₁ (x−a).

Il n. ordinario si riconosce dal fatto che si ha

c₁≠c′₁, c₂≠0, c′₂≠0;

il flecnodo dal fatto che c₁≠c′₁, c₂=0, c′₂≠0; il biflecnodo dal fatto che c₁≠c′₁, c₂=c′₂=0; il tacnodo dal fatto che c₁=c′₁, c₂≠c′₂; infine, l’oscnodo dal fatto che c₁=c′₁, c₂=c′₂.

Teoria dei nodi

fig. 2

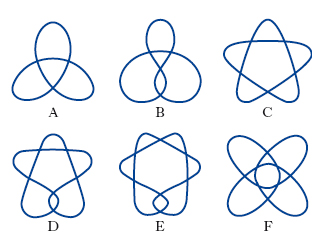
In topologia, studia le proprietà geometriche, in particolare i gruppi di omotopia dell’insieme complementare in R³, di un n. o circuito annodato, ossia di una curva semplice chiusa non riducibile con deformazione continua a una circonferenza (n. banale). Tutti i n. sono omeomorfi tra loro, tuttavia a causa della diversa maniera con cui si immergono in R³ essi vengono classificati in tipi di n. equivalenti o dello stesso tipo, che si possono cioè corrispondere mediante un omeomorfismo. La proiezione ortogonale su un piano permette di classificare i diversi tipi di n.: ne esistono un solo tipo per i n. con 3 o 4 autointersezioni (sul piano), 2 e 3 tipi per quelli con 5 o 6 autointersezioni, 7 e 21 per quelli con 7 o 8 autointersezioni rispettivamente (in fig. 2 sono dati alcuni esempi). Tuttavia, anche se è stato possibile distinguere i vari tipi con al massimo 10 autointersezioni, una classificazione completa di tutti i possibili casi è tuttora sconosciuta. A partire dagli anni 1980, la teoria dei n. ha mostrato, oltre al notevole interesse intrinseco, un numero sempre crescente di punti di contatto con svariate problematiche della fisica. Ciò non sorprende, se si considera che la teoria dei n. ha avuto origine proprio da un problema di fisica. Nel 19° sec. lord Kelvin ideò una teoria, la cosiddetta teoria degli atomi vortice, in cui gli atomi erano considerati come mulinelli (vortici) nell’etere (onnipervasivo substrato fluido dello spazio a tre dimensioni). Kelvin immaginava questi mulinelli come anelli di fumo che fossero annodati individualmente ed eventualmente l’uno con l’altro a formare le molecole. Questa teoria coinvolse alcuni matematici in un progetto per la compilazione di tavole di tutti i n. topologicamente distinti. La teoria degli atomi vortice scomparve quando la teoria di Einstein della relatività speciale e i risultati dell’esperimento di Michelson-Morley mostrarono che lo ‘spazio vuoto’, qualunque ne fosse la natura, non poteva essere considerato analogo a un fluido onnipervasivo.

La correlazione tra la teoria dei n. e la fisica moderna fu stabilita all’inizio degli anni 1980, quando L.H. Kauffman riuscì a trovare il modo di descrivere il polinomio di Alexander (e più tardi il polinomio di Jones) nella forma di una funzione di partizione della meccanica statistica, e V. Jones scoprì invarianti del tutto nuovi di n. e link (un link è l’unione di un numero finito di n. che non abbiano tratti di corda in comune), direttamente correlati a problemi di meccanica statistica. Pochi anni più tardi, E. Witten mostrò come tutte queste costruzioni potessero essere comprese in termini di teoria quantistica dei campi, dando con ciò origine al nuovo settore di studio riguardante la topologia quantistica e la teoria topologica dei campi quantizzati.

Topologia e diagrammi

fig. 3

Le informazioni topologiche sui n. si possono ottenere direttamente dai loro diagrammi. Una proprietà di un n. è detta topologica se non dipende dal materiale con cui il n. è costruito né da quanto questo materiale sia stirato o piegato, purché non venga lacerato. Per non perdere il n. nel corso di questo processo di deformazione adottiamo la convenzione, usuale nella teoria dei n., che il n. si trovi su un anello chiuso. Il n. a trifoglio, mostrato nella fig. 3, è il primo esempio di anello chiuso annodato. Un n. presentato come anello chiuso è un oggetto che può essere spostato e rigirato nello spazio in molte forme diverse ma topologicamente equivalenti. Il numero potenzialmente infinito di versioni di un dato n. o link fa emergere un vero problema matematico.

Dire che un anello è annodato significa dire che nessuna delle infinite forme che esso può assumere è quella di un anello non annodato. Il risultato chiave che sta alla base di una teoria combinatoria dei n. è il teorema di Reidemeister, secondo cui due diagrammi rappresentano lo stesso tipo di n. se, e soltanto se, si possono ottenere l’uno dall’altro tramite una successione finita di deformazioni speciali, dette mosse di Reidemeister. Il risultato del teorema di Reidemeister è che i problemi topologici sui n. possono tutti essere riformulati in termini della matematica di questi tre diagrammi nel piano. Le mosse di Reidemeister colgono in modo combinatorio la nozione di isotopia ambiente (cioè di equivalenza topologica) dei n. nello spazio tridimensionale. Questo significa che, pensando ai diagrammi di n. come fotografie istantanee, se due n. si possono trasformare l’uno nell’altro allora anche le loro istantanee possono essere trasformate l’una nell’altra tramite una sequenza finita di mosse di Reidemeister. L’importanza di questo risultato è che il problema della classificazione topologica di n. e link nello spazio tridimensionale può essere riformulato nei termini di un problema di classificazione dei diagrammi di link, a meno della relazione di equivalenza generata dalle mosse di Reidemeister. Utilizzare le mosse di Reidemeister come base teorica per sviluppare la teoria dei n. è un compito laborioso: da principio non è affatto chiaro come ottenere informazioni che siano invarianti rispetto alle mosse. Ed è l’invarianza a essere importante: si vorrebbero poter calcolare numeri (o entità algebriche come polinomi) a partire da un qualsiasi diagramma di link in modo tale che questi numeri non cambino quando un diagramma è modificato tramite una mossa di Reidemeister. Trovare tali invarianti significa trovare le informazioni topologiche sui n. o sui link. L’esempio più semplice di un tale invariante è il ‘numero di allacciamento’ di due curve: esso misura quante volte una curva orientata si avvolge intorno a un’altra. Se le curve A e B sono rappresentate in un diagramma di link a due componenti, il numero di allacciamento Al è definito dalla formula

Al (A,B) = (1/2) ∑_x e(x)

fig. 4A

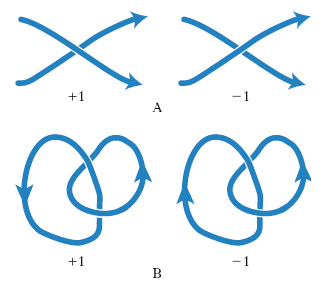
dove la somma è eseguita al variare degli incroci x di A con B, ed e(x) indica il segno dell’incrocio, definito come +1 o −1 secondo la convenzione descritta nella fig. 4A. Naturalmente, due anelli allacciati semplicemente hanno numero di allacciamento +1 o −1, come mostrato nella fig. 4B. Il numero di allacciamento è invariante rispetto alle mosse di Reidemeister, cioè non può esistere nessuna successione di mosse di Reidemeister che trasformi due anelli allacciati in due anelli separati, poiché il numero di allacciamento di due anelli separati è nullo.

fig. 5

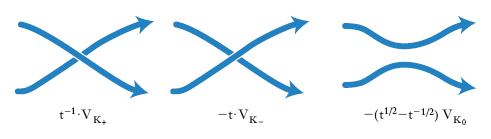
Un invariante di n. e link di natura alquanto diversa è quello polinomiale scoperto da Jones, indicato generalmente con V_K(t); si tratta di un polinomio nella variabile t^1/2 e nella sua inversa t^−1/2 (ciò si esprime dicendo che V_K(t) è un polinomio di Laurent in t^1/2). Per esso si considerano i seguenti assiomi: 1) se due link orientati K e K′ sono collegati da un’isotopia ambiente, allora V_K(t)=V_K′(t); 2) se U è un anello snodato, allora V_U(t)=1; 3) siano K₊, K₋ e K₀ tre link orientati con diagrammi che differiscono, come specificato nella fig. 5, solo in una piccola regione del piano, nella quale K₊ e K₋ hanno un incrocio e K₀ non ne ha; allora vale la formula

t⁻¹ ∙ V_K+(t)−t ∙ V_K−(t) = (t^1/2−t^−1/2)V_K0(t).

Questo schema di assiomi per il polinomio di Jones è simile a quello utilizzato da J.H. Conway per una generalizzazione del classico polinomio di Alexander. Gli assiomi per V_K(t) sono una conseguenza del metodo di definizione originale usato da Jones per il suo invariante; il cammino che lo portò alla scoperta di questo invariante cominciò con lo studio delle algebre di von Neumann (una branca dell’algebra con collegamenti diretti alla teoria dei quanti e alla meccanica statistica) e si concluse con lo studio di trecce, n. e link. Il polinomio di Jones ha un significato completamente diverso dal polinomio di Alexander-Conway, sebbene possa essere assiomatizzato in maniera molto simile. Un fatto che ha reso subito il polinomio di Jones una scoperta estremamente interessante per i teorici dei n. è che esso permette di individuare la differenza tra molti n. e le loro immagini speculari. In seguito sono emerse altre interessanti proprietà: per es., esso è stato uno strumento chiave per la dimostrazione di proprietà dei link alternanti (e nelle loro generalizzazioni) che erano state congetturate già nel 19° sec.; a tutt’oggi non sono noti esempi di n. di cui il polinomio di Jones non riconosca l’annodamento. Ciò suggerisce la seguente congettura. Se un singolo anello di un n. K è effettivamente annodato, allora V_K(t) non è uguale a 1. In altre parole, è concepibile che il polinomio di Jones sia capace di determinare la proprietà di effettivo annodamento. È tuttavia noto che esso non è uno strumento di classificazione completo: esistono coppie di n. che hanno il medesimo polinomio di Jones ma che non possono essere collegati da un’isotopia ambiente, ovvero sono topologicamente diversi. Una tale coppia è costituita dai n. di Kinoshita-Terasaka e di Conway. Il calcolo del polinomio di Jones, a partire dai suoi assiomi, non spiega perché questo invariante ‘funzioni’. L’analisi di questo metodo di calcolo permette di dimostrare che esso dipende dalle scelte fatte e che fornisce informazioni sul n. e sui link in esame. Un metodo alternativo porta a un’elegante formulazione del polinomio di Jones in termini di una somma sugli stati del diagramma. In tale formulazione il polinomio è ben definito fin dall’inizio e si vede che l’invarianza topologica nasce dall’aggiustamento di alcuni parametri di funzioni ben definite.

Secondo gli sviluppi più recenti di questo approccio, si tende a considerare il diagramma di un n. analogo a un sistema fisico del quale viene calcolata una funzione di partizione o somma sugli stati. La funzione di partizione è una somma di certe valutazioni su tutti i possibili stati del sistema, dove il termine stato va inteso in modo opportuno. Gli stati non sono le varie configurazioni che vengono assunte nel corso di un’evoluzione (deformazione topologica) a partire da una data situazione: sono invece modi di configurare la situazione presente. La funzione di partizione fornisce informazioni sulle evoluzioni topologiche del sistema senza che queste compaiano effettivamente.

fig. 6

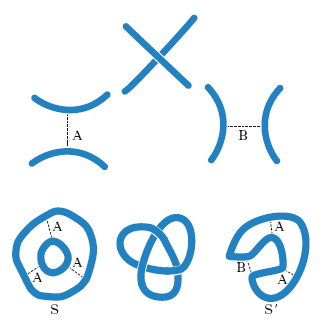
Per fornire un esempio di come si possa mettere in pratica quest’idea della valutazione, descriviamo ora la più semplice somma sugli stati per n. e link che risulti significativa, cioè il polinomio bracket (termine quest’ultimo che indica le particolari parentesi ad angolo introdotte da P.A.M. Dirac: ➔ bra; ket). Prendiamo in considerazione n. e link non orientati, e a ogni incrocio di un diagramma associamo due stati che identifichiamo con le etichette A e B, come mostrato nella fig. 6 (in alto). Nello stato A vengono connesse tra loro le regioni del piano spazzate da una rotazione in senso antiorario dell’arco che sta sopra, mentre nello stato B vengono connesse quelle spazzate da una rotazione in senso orario del medesimo arco. Uno stato S di un diagramma K consiste nella scelta di uno stato locale per ciascuno dei suoi incroci, cosicché un diagramma con n incroci avrà 2ⁿ stati. Due stati S e S′ del diagramma del n. a trifoglio sono indicati nella fig. 6 (in basso). Utilizzeremo due valutazioni per uno stato S, indicate rispettivamente con ‹K|S› e con ∥S∥. Quest’ultima è chiamata norma dello stato ed è definita come il numero di curve chiuse che compongono S, «meno uno»; così nell’esempio di cui sopra si ha ∥S∥=1 e ∥S′∥=0. La valutazione ‹K|S› è definita come il prodotto di tutte le etichette A o B nello stato: nell’esempio precedente si ha allora ‹K|S›=A³ e ‹K|S′›=A²B. Utilizzando variabili A, B e d definiamo la somma sugli stati associata al diagramma K mediante la formula seguente:

‹K› = ∑_S ‹K|S› ∙ d^∥S∥.

In altre parole, per ogni stato S prendiamo il prodotto delle etichette che si trovano in S moltiplicato per d, elevato a ∥S∥. Questa relazione sugli stati (che esprime il fatto che stiamo sommando su tutti i possibili stati utilizzando i pesi locali A e B) è invariante rispetto alle mosse di Reidemeister purché si scelga B=1/A, d=−(A²+B²) e si effettui una normalizzazione, quindi permette di ottenere informazioni topologiche su n. e link. Gli invarianti costruiti secondo questo schema si sono rivelati, nella pratica, di grande interesse: per es., grazie a essi è possibile distinguere molti n. dalle loro immagini speculari e accade spesso che il calcolo del bracket sia sufficiente a mostrare se un certo n. è effettivamente annodato.

fig. 7A

fig. 8

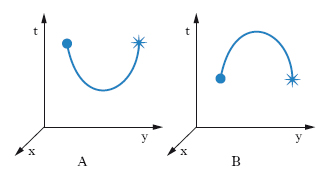
Questo approccio alla teoria dei n. considerando il modello bracket del polinomio di Jones è suscettibile di diverse interpretazioni, una delle quali evidenzia la connessione tra topologia e meccanica quantistica. Immaginiamo che lo spazio sia bidimensionale, invece che tridimensionale come quello in cui viviamo. Poiché lo spazio occupa due sole dimensioni, possiamo immaginare lo spazio-tempo come tridimensionale, generato da un piano che si muove, e le tracce di punti in moto nel piano diventano le linee di universo dei punti nello spazio-tempo. Consideriamo alcuni esempi semplici. Potrebbe accadere di vedere due particelle che girano l’una attorno all’altra: nella descrizione spaziotemporale di questo moto vediamo le due linee di universo che si avvolgono l’una intorno all’altra a formare una treccia semplice. Ancora, può accadere che l’energia dello spazio vuoto dia origine a due particelle: la linea di universo corrispondente alla creazione di una coppia di particelle, come si vede nella fig. 7A, appare come una coppa, ovvero una curva con un minimo a un determinato istante. Ma può anche accadere che due particelle si annichilino a vicenda: nello spazio-tempo tridimensionale la sparizione di una coppia di particelle è rappresentata da un cappello, come mostrato nella fig. 7B, vale a dire da una curva che presenta un massimo a un determinato istante. Qualsiasi processo elementare di interazione si riflette, nel nostro spazio-tempo a tre dimensioni, in un attorcigliamento (a destra o a sinistra), una coppa o un cappello, il cui susseguirsi determina, nello spazio-tempo, n. e link, come mostrato nella fig. 8.

Nella meccanica quantistica ci si può porre la domanda: qual è l’ampiezza di probabilità che certe particelle appaiano dal vuoto, si muovano nello spazio-tempo tridimensionale seguendo il cammino corrispondente a un certo n. o link e poi se ne tornino nel vuoto? La risposta a questa domanda è che tale ampiezza è proprio un valore del polinomio bracket del nodo. In meccanica quantistica nella notazione ‹a|b› di Dirac ‹a| e |b› sono rispettivamente un vettore e un vettore covariante, mentre ‹a|b› è il valore di ‹b| in |a›, dunque uno scalare, generalmente complesso, che può essere interpretato come l’ampiezza di probabilità per un processo con stato iniziale ‹a| e finale |b›. La notazione di Dirac pone in risalto il legame tra l’interpretazione probabilistica dell’ampiezza e la struttura di spazio vettoriale dello spazio degli stati di un sistema quantistico. La relazione tra la teoria dei quanti e la topologia è messa in evidenza dalle considerazioni che ruotano intorno al bracket di Dirac: si può dire che il bracket di Dirac funge da intermediario tra la notazione e l’algebra lineare, e che la connessione tra la meccanica quantistica e la topologia si ottiene estendendo la notazione di Dirac.

Metrologia

Unità di misura della velocità di una nave: corrisponde alla velocità di un miglio nautico internazionale (1852 m) all’ora, pari a 0,51444 m/s.

Tecnica

fig. 9

Intreccio di uno o più tratti di corda, consistente in un avvolgimento del tratto su sé stesso o in un suo collegamento con un altro tratto o con oggetti diversi, e avente lo scopo di realizzare, a seconda dei casi, un accorciamento e ingrossamento della corda, un cappio atto ad agganciare o a serrare, una giunzione di due o più capi, una legatura fissa o scorsoia. Secondo il modo dell’avvolgimento si hanno vari tipi di nodi (fig. 9), usati nell’alpinismo, nella navigazione, nell’attrezzatura per la pesca e in altre attività che comportano l’uso di fili e corde, talvolta chiamati con il nome di chi li ha inventati, spesso indicati con nomi diversi o con qualifiche che ne precisano il settore di attività. Nell’attrezzatura navale si usano correntemente n. di vario tipo per scopi diversi: per evitare lo sciogliersi dei legnoli (n. semplice, n. diamante, vari tipi di bottone ecc.); per accorciare un cavo o per crearvi un ingrossamento locale (n. margherita, n. di Savoia o d’amore o a otto, n. del frate o del cappuccino ecc.); per unire insieme due cavi (n. piano, n. inglese o del pescatore, n. vaccaio o di tonneggio, n. di matafione, n. di scotta, o gruppo di bandiera ecc.); per imbragare o abbracciare un oggetto, assicurare cavi d’ormeggio, collegare una cima a un gancio o a un anello (n. a bocca di lupo, n. parlato, n., o gruppo, d’ancorotto, gassa d’amante semplice, doppia, scorsoia ecc.); caratteristiche comuni a tutti i n. marinareschi sono la sicurezza sotto sforzo e la facilità a essere sciolti quando non sono più in tensione. Nell’alpinismo per legarsi in cordata, con legatura intorno alla vita o collegando la corda all’imbragatura, si può usare il n. delle guide, in pratica una semplice asola; per assicurazione o per autoassicurazione il n. del barcaiolo, ossia il n. parlato dell’attrezzatura navale; per sicurezza nella discesa in corda doppia, per risalire lungo la corda, per effettuare operazioni di soccorso si usano n. autobloccanti, come il n. Prusik, il n. Marchand, il n. valdostano ecc., realizzati, con spezzoni di cordino sulla corda di cordata, in modo da scorrere se impugnati sugli avvolgimenti che li costituiscono e bloccarsi se l’asola che ne esce è sottoposta a trazione.

In scienza delle costruzioni, nelle travature reticolari, il punto ideale nel quale concorrono gli assi delle aste costituenti la travatura. Nelle travature metalliche, in corrispondenza dei n., le aste concorrenti sono congiunte mediante piastre, alle quali sono fissate con chiodatura, con saldatura o, più raramente, in costruzioni smontabili, con bulloni. Ai fini della determinazione degli sforzi agenti sulle singole aste, i n. vengono schematizzati come cerniere; ciò non è rigorosamente esatto, manifestandosi ai n. momenti d’incastro che, per l’entità non elevata, vengono generalmente trascurati. Si dicono metodi dei n., i metodi atti a risolvere una travatura reticolare in base alla considerazione dell’equilibrio dei singoli n. del sistema.

In una rete elettrica, ogni punto nel quale concorrono tre o più rami. Sono n. indipendenti tutti i n. della rete meno uno, scelto arbitrariamente (quest’ultimo corrisponde al n. connesso a massa e al quale vengono riferiti i potenzia;li degli altri n.). La 1ª legge di Kirchhoff (➔ Kirchhoff, Gustav Robert) è anche detta legge dei n.; a partire da essa, è possibile analizzare in modo sistematico un circuito elettrico mediante il metodo dei nodi.