quantistico

In fisica e chimica, si dice di ciò che concerne la teoria dei quanti (➔ meccanica).

Chimica

La chimica q. è la parte della chimica teorica che applica le leggi della meccanica q. per interpretare i fenomeni chimici. La teoria dei quanti nelle sue applicazioni alla chimica ha consentito di dare una chiara interpretazione degli stati elettronici degli atomi e delle molecole, della risonanza, giungendo fino allo studio della velocità delle reazioni. Il capitolo più importante della chimica q. è quello riguardante lo studio della natura dei legami (➔ orbitale; legame chimico), che ha consentito una soddisfacente trattazione quantitativa della struttura di molecole semplici e anche della struttura di altre molecole più complesse, in forma però meno rigorosa.

Fisica

Elettronica quantistica

L’elettronica q. è la parte della fisica che si occupa dei dispositivi elettronici in cui hanno essenziale rilevanza effetti q. (laser, maser, diodi tunnel ecc.) e dei relativi fenomeni, che comportano interazioni fra la materia e radiazioni elettromagnetiche (irraggiamento per eccitazione, assorbimento, interazioni fotone-fonone ecc.).

fig. 1

fig. 2

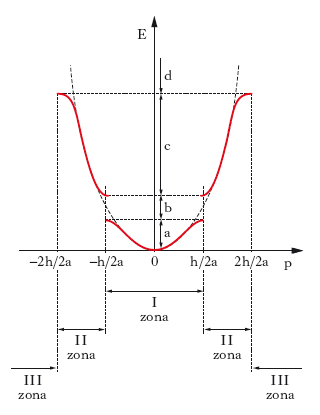
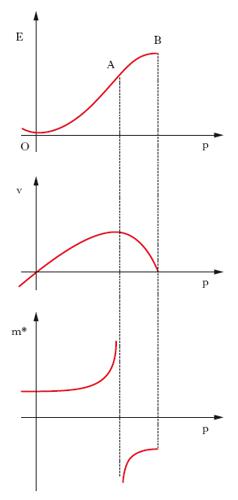
La teoria q. delle bande spiega in termini rigorosi la formazione di bande di livelli energetici per gli elettroni di un solido. Il comportamento degli elettroni in un solido deve essere studiato in termini di evoluzione della loro funzione d’onda, che si ottiene risolvendo, sotto opportune condizioni, l’equazione di Schrödinger: in particolare, possono essere determinate, per il caso qui considerato di un elettrone in un solido cristallino, descrivibile come uno spazio nel quale il potenziale elettrico varia periodicamente, soluzioni sotto forma di onde progressive (funzioni di Bloch). Indicata con λ = h/p la lunghezza d’onda di de Broglie dell’elettrone (pari al rapporto tra la costante di Planck h e la quantità di moto p) nel caso semplice di un reticolo cristallino parallelepipedo a celle cubiche di spigolo a, riferito a un triedro cartesiano (O,x,y,z), si ha λ_x=a N_x/n_x, essendo N_x il numero di atomi lungo la direzione x e n_x=0, 1, 2 ..., e analogamente per λ_y e λ_z; è dunque p_x=±hn_x/(aN_x), e analogamente per p_y e p_z. Le grandezze p_x, p_y, p_z, ora definite, sono dette quasi-impulsi o, con terminologia derivata dall’inglese, momenti di cristallo degli elettroni. Il modulo quadrato della funzione d’onda fornisce la densità di probabilità di presenza degli elettroni ed è massimo nei punti in cui è minima l’energia degli elettroni, conformemen­te al fatto che questi ultimi tendono a disporsi nello stato di energia minima; conseguentemente, due successivi ventri della funzione d’onda debbono distare tra loro di a o, più in generale, di a/k, con k intero; si ha dunque λ_x/2=a/k e p_x=±k h/(2a), se per semplicità ci si limita a considerare quel che succede lungo l’asse x. Si può anche dire che per valori di p_x abbastanza lontani da tali valori singolari, la funzione d’onda degli elettroni ha la forma analitica di un’onda progressiva, mentre ha una forma stazionaria quando p_x è pari, in valore assoluto, a un multiplo intero di h/(2a). L’andamento che in definitiva si ottiene per l’energia E degli elettroni al variare del loro momento di cristallo p è riportato nella fig. 1; la curva tratteggiata, alla quale si appoggiano, per così dire, i vari tratti del diagramma E(p), è la parabola che si avrebbe nel caso in cui si considerasse la sola energia cinetica (E=p²/2m). Come risulta dalla medesima fig., la discontinuità corrispondente alla transizione dal regime a onde progressive al regime a onde stazionarie genera intervalli proibiti di energia, cioè bande proibite (b, d ecc.), tra intervalli consentiti di energia, cioè tra bande permesse (a, c ecc.). Di tale stato di cose si può anche dare una rappresentazione geometrica nello spazio dei momenti, cioè in un sistema di riferimento (O, p_x, p_y, p_z): si ottengono così figure, nel cui interno cadono i punti rappresentativi dei vari elettroni, che sono dette zone di Brillouin, di cui la prima è relativa all’intervallo −h/2a-h/2a, la seconda agli intervalli −2h/2a-−h/2a, h/2a-2h/2a, e così via (fig. 1), dei valori di p_x, p_y, p_z. Se una banda o, se si vuole, una zona di Brillouin, è parzialmente occupata, gli elettroni in essa presenti possono muoversi sotto l’azione di un campo elettrico, con una velocità v che vale ∂E/∂p. Nella fig. 2 è riportato l’andamento di E e di v al variare di p, riferito alla prima soltanto delle zone di Brillouin. Salta agli occhi il fatto che, se si interpreta p come una quantità di moto, nell’intervallo AB la quantità di moto va crescendo mentre la velocità va diminuendo; per spiegare ciò si è costretti a sostituire la massa reale m dell’elettrone con una massa efficace m*, il cui andamento con p è indicato nella fig. 2, in basso. Gli elettroni cui è dovuta la conduzione sono usualmente su livelli abbastanza vicini al limite inferiore della banda, cioè compresi nel tratto OA della curva E(p) e più vicini a O che ad A: in tali condizioni m* è positiva e generalmente poco diversa da m. Nel caso invece che gli elettroni cui è dovuta la conduzione siano in livelli prossimi al limite superiore della banda, cioè compresi nel tratto AB della curva E(p), più vicini a B che ad A, m* è negativa; alla situazione effettiva può pensarsi sostituita una nuova situazione, in cui si pensa di introdurre nella banda un certo numero di elettroni e altrettante cariche fittizie positive (lacune elettroniche) in modo da saturare la banda e da immaginare la conduzione dovuta al moto delle cariche fittizie anzidette.

Teoria q. dei campi

La proprietà che caratterizza la teoria q. dei campi è di fornire schemi dinamici q. consistenti con la relatività ristretta di Einstein. Ciò impone di trattare le forze come gradi di libertà dinamici e non come funzioni dirette delle coordinate dei corpi. Per questo vengono introdotti i campi di forza (come i campi elettromagnetici) soggetti alle loro equazioni di evoluzione (le equazioni di Maxwell) e quindi caratterizzati da una dinamica autonoma, che si evidenzia nella propagazione libera (campo libero, di cui le onde elettromagnetiche costituiscono l’esempio più comunemente noto). In termini più generali, la teoria q. dei campi nasce dalla necessità di soddisfare i principi fondamentali di causalità, per il quale nessun effetto può precedere la propria causa, e di positività dell’energia. Nel caso della propagazione libera, il processo di quantizzazione fa apparire i quanti relativi ai differenti modi di oscillazione del campo d’onda (nel caso elettromagnetico, i fotoni). A causa dell’invarianza per traslazioni e rotazioni, che caratterizza naturalmente il campo libero, ai quanti sono associati, oltre all’energia, un impulso (quantità di moto) e un momento angolare (momento della quantità di moto). La relazione tra energia e impulso, trattandosi di una teoria relativistica, deve necessariamente corrispondere a quella di una particella di massa definita, perché questa è l’unica relativisticamente invariante. Inoltre, dato che la teoria relativistica dei campi q. si basa su due costanti universali, cioè la velocità della luce nel vuoto (c) e la costante di Planck (h), la massa m delle particelle definisce naturalmente una lunghezza, ℏ/(mc)=λ_c, con ℏ costante di Planck ridotta, che si identifica con il raggio d’azione del campo associato. Nasce così il concetto di particella elementare caratterizzata unicamente dalla massa e dal momento angolare intrinseco (spin).