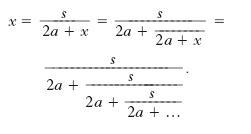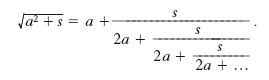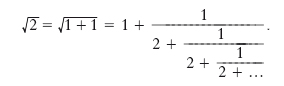radice

Anatomia e medicina

La porzione d’impianto di un organo in accrescimento (r. del pelo, r. dell’unghia), oppure l’elemento morfologico che dà fissità a un organo (r. del dente, della lingua) o che ne costituisce il tratto iniziale (r. dei nervi), o, infine, struttura che dà origine ad altre (r. della vena porta).

In particolare le r. dei nervi sono i tronchi nervosi in continuità con encefalo o midollo, costituiti dalle fibre nervose che penetrano nel sistema nervoso centrale (fibre sensitive) o ne emergono (fibre motrici). Le r. dei nervi encefalici hanno origine e decorso differenti fra loro. Le r. dei nervi spinali emergono appaiate (r. anteriore e posteriore) da ciascun metamero. In prossimità del midollo hanno struttura filamentosa, mentre acquistano l’aspetto di cordone in vicinanza della teca vertebrale. La r. posteriore (sensitiva), a differenza di quella anteriore (motoria), presenta nel suo spessore un ganglio (ganglio spinale), in cui si interrompono le fibre radicolari provenienti dalla periferia. Il decorso delle r. è obliquo verso il basso (a eccezione delle prime tre cervicali): tale obliquità è massima per le ultime che formano la cauda equina. La pia madre le riveste lungo tutto il decorso. La radicolopatia è un processo patologico a carico di una r. spinale. Responsabili di radicolopatie sono: fattori infiammatori (infettivi: batterici, virali e parassitari), allergici, compressivi (neoplasie, ernie discali, aneurismi, ascessi ecc.), traumatici (ferite, fratture), vascolari (processi emorragici, trombotici o embolici), tossici, dismetabolici o malformativi. I sintomi sensitivi (dolori, parestesie ecc.) sono i più precoci e invalidanti, mentre quelli motori, neurovegetativi e trofici sono più tardivi. Si definiscono anestesia e paralisi radicolare i deficit, rispettivamente di senso e di moto, dovuti alla lesione di una r. spinale. La radicolite è l’interessamento infiammatorio a carico di una o più (poliradicolite) r. spinali; la radicoloneurite il processo infiammatorio che colpisce la r. spinale e i nervi che ne originano; dato che sussiste una compartecipazione del rivestimento meningeo, viene di preferenza usato il termine di meningoradicolite (➔ meninge). La radicolografia è il procedimento di visualizzazione radiografica delle r. spinali lombosacrali, eseguito iniettando un mezzo di contrasto per via lombare; è impiegato soprattutto nello studio della patologia discale. Cisti radicolare Tumore dei mascellari localizzato in prossimità dell’apice d’una r. dentaria. Rappresenta l’evoluzione di un granuloma apicale.

Botanica

La parte inferiore del corpo (cormo) delle piante superiori (Pteridofite e Fanerogame) che ha la duplice funzione di fissare la pianta al terreno e di assorbire da questo l’acqua e i sali necessari al suo nutrimento. In generale la r. differisce dal fusto (➔ rizoma) perché non porta mai appendici simili alle foglie e ha l’apice protetto dalla cuffia; inoltre, manca di gemme, di stomi e di cuticola.

Origine

La r. è la prima parte dell’embrione che esce dal seme germinante dirigendosi verso il basso, in quanto ha geotropismo positivo. Nell’embrione è rappresentata da un abbozzo, detto radichetta, di forma di solito cilindrico-conica. La r. che si sviluppa dalla radichetta è detta r. primaria; questa è cilindrica o in forma di cono molto lungo e sottile; la r. primaria di norma dà origine, ai lati, a r. secondarie; queste sono disposte in serie longitudinali, in numero di norma costante nelle singole famiglie o specie: così 4 file equidistanti in molte Fabacee, 4 file avvicinate a 2 a 2 nelle Brassicacee, 3 nel pisello, 5 nella fava ecc. Dalle r. secondarie si dipartono r. di terzo ordine e così via, costituendo un complesso detto apparato radicale. Sia i rami di vario ordine della r. primaria sia le r. caulogene hanno origine interna e precisamente si originano al livello del periciclo e, accrescendosi, attraversano la corteccia primaria, lacerandone gli strati più esterni.

Struttura

fig. 1

fig. 2C

Parti della radice

L’estremità delle r. comprende un apice vegetativo, formato da meristemi, con cellule in attiva divisione, dalle quali hanno origine le cellule che formeranno i tessuti definitivi; esso è nascosto e protetto contro le possibili offese da un rivestimento fatto a guisa di dito di guanto, detto caliptra, o pileoriza o cuffia radicale, originato da un proprio meristema (caliptrogeno). La cuffia risulta di molte cellule, di cui le più esterne, che sono le più vecchie, gradatamente si logorano e muoiono. La cuffia è di solito molto piccola. Anche l’apice è molto breve. A questo segue una regione lunga circa un cm, detta regione di accrescimento, dove le cellule già formatesi nell’apice aumentano di dimensioni. Segue la regione pilifera o assorbente, detta così perché molte delle sue cellule superficiali (fino a più di 400 per mm²) si estroflettono, formando ciascuna un piccolo budello provvisto di parete sottilissima (pelo radicale), attraverso cui l’acqua e le sostanze discioltevi sono succhiate dalla radice (fig. 1). Appunto per aumentare la superficie assorbente, dette cellule si allungano fino a formare dei peli, i quali si adattano strettamente alle minutissime particelle del terreno. È da notare che l’assorbimento, talvolta molto considerevole, avviene soltanto in questa regione della radice. I peli ben presto si logorano e sono sostituiti continuamente da altri peli che si formano in prossimità dell’apice (fig. 2C).

Struttura primaria

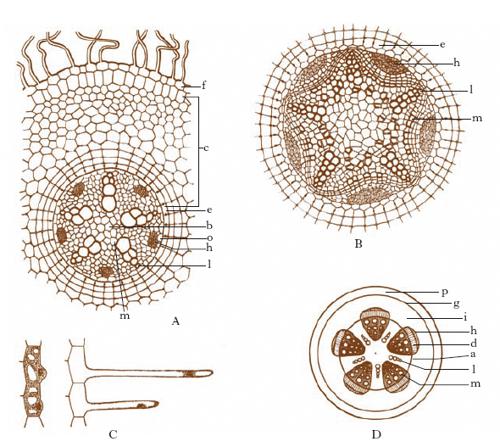
A differenza del fusto, la r. presenta la medesima struttura in tutti i gruppi delle Cormofite. In una sezione trasversa si osservano, come nel fusto, tre regioni: l’epidermide, la corteccia primaria o cilindro corticale, la stele, o cilindro centrale (fig. 2A). L’epidermide è di un solo strato, è priva di stomi e di cuticola ed è munita di numerosi peli assorbenti (per l’epidermide pluristratificata che forma il velo radicale in certe Orchidacee, ➔ velo). Essa è di breve durata: all’epoca della sua scomparsa, le sottostanti cellule della corteccia suberificano le pareti e costituiscono un tessuto di protezione detto esoderma. La corteccia consta di parenchima ed eventualmente di fibre, e presenta nettamente differenziato lo strato più interno, che prende il nome di endoderma. La stele è del tipo dell’actinostele, al centro c’è il midollo ed esternamente è delimitata dal periciclo; nel parenchima fondamentale si trova una cerchia di fasci semplici alternati, cioè ogni legnoso si alterna a uno fibroso (carattere anatomico proprio della radice). I fasci legnosi spesso sono sviluppati in senso radiale verso il centro (lamine vascolari) o addirittura si congiungono al centro formando come un unico fascio stellare (e allora manca il midollo); da questa disposizione la stele della r. ha preso il nome di actinostele, vale a dire stele raggiata. Il numero dei fasci legnosi (e rispettivamente cribrosi) varia secondo la specie, da uno a parecchi, e le rispettive r. si dicono monarche, diarche, triarche, tetrarche, poliarche. Nell’ipocotile, regione situata fra la r. e l’inserzione dei cotiledoni, si osserva il passaggio dalla struttura del fusto (che ha fasci composti) a quella della r. (che ha fasci semplici), poiché i fasci del fusto sono in continuità con quelli della radice.

Struttura secondaria

Le Dicotiledoni con struttura secondaria nel fusto e tutte le Gimnosperme presentano anche nella r. struttura secondaria, determinata dall’attività di un meristema completamente secondario (differenza rispetto al fusto), il quale si origina dal parenchima fondamentale e precisamente all’interno dei fasci cribrosi e all’esterno di quelli legnosi, avendo prima un decorso sinuoso nella sezione trasversale, che poi diventa gradatamente circolare. Questo meristema è detto cambio e, come quello del fusto, dà origine a numerosi elementi verso l’interno e verso l’esterno: in corrispondenza dei fasci legnosi forma solo parenchima, ossia un raggio midollare secondario, cosicché dopo un certo tempo, con l’accrescersi della r., i fasci legnosi primari, costituiti da pochi elementi, vengono a trovarsi isolati in mezzo al parenchima, in fondo ai raggi midollari secondari. In corrispondenza dei fasci cribrosi, invece, il cambio si comporta come nel fusto: esso schiaccia verso l’esterno i fasci cribrosi primari e produce verso l’esterno corteccia secondaria, verso l’interno legno secondario (fig. 2B e D). In molte piante tutto l’anello di cambio produce libro e legno, dunque anche in corrispondenza dei raggi midollari primari, cosicché si forma una zona libro-legnosa continua. Anche nella r. il cambio è attivo solo nella stagione favorevole, tuttavia nella r. non si osservano cerchie annuali distinte. Verso la periferia della r. si origina più o meno presto un fellogeno (dalla corteccia primaria o dal periciclo), il quale genera sughero e felloderma. Anche nella r. si formano lenticelle che assicurano gli scambi gassosi con l’ambiente esterno. Nelle Monocotiledoni la struttura secondaria nella r. è ancora più rara che nel fusto: il meristema secondario si origina nella corteccia primaria o in alcune specie dal periciclo, e le sue produzioni sono simili a quelle secondarie del fusto monocotile.

Tipi di r. e loro metamorfosi

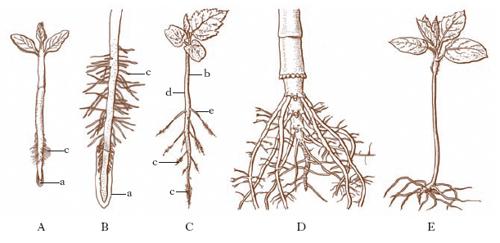
Per l’aspetto esterno si distinguono: r. a fittone, se la r. principale si accresce molto, specialmente in lunghezza, in confronto ai suoi rami; r. fascicolate, se i rami si accrescono notevolmente in modo da eguagliare o superare in sviluppo la r. principale, oppure quando molte r. caulogene si originano una accanto all’altra (fig. 1).

Anche la r., come gli altri due membri morfologici del cormo (fusto e foglie), presenta in certe piante modificazioni profonde rispetto alla r. normale. Si chiama radicoma il complesso degli organi vegetali che hanno natura morfologica di r., anche se non ne hanno la funzione. I tipi principali di r. metamorfosate sono: eterorrizia (edera), appiattimento (Podostemonacee), tuberizzazione (asfodelo), cirrazione (vaniglia), spinificazione (alcune Palme), natatoi (Jussieua), r. epigee e aeree, che si sviluppano al di sopra del suolo.

È detta radicosità la presenza di r. laterali ingrossate nella barbabietola, dovuta a una reazione a lesioni dei fasci vascolari. Essa incide negativamente sul raccolto, perché durante l’estrazione dal terreno una parte della barbabietola va perduta, e danneggia anche la successiva lavorazione nello zuccherificio. Il radicotubero è l’ingrossamento, simile a un tubero, di parte della r., finalizzato all’accumulo di sostanze di riserva, come avviene, per es., nell’asfodelo.

Linguistica

Elemento costituito da uno o più fonemi, non ulteriormente analizzabile né riducibile morfologicamente e semanticamente, presente come nucleo concettuale centrale in tutte le parole di una stessa famiglia etimologica. La r., che talvolta è indicata anche con i termini più generici di base o semantema, può essere isolata eliminando, in una parola o in una serie di parole etimologicamente connesse tra loro, tutti gli elementi individuabili come affissi morfematici; l’individuazione della r. può essere inoltre effettuata su un piano sincronico, e cioè con riferimento a una data fase di una lingua o di una famiglia di lingue, o diacronico, e cioè risalendo alle diverse fasi di una lingua o di lingue tra loro imparentate. Così una ricerca sincronica può isolare nelle voci it. correre, corrente, corridore, corridoio, corriere, corsa, corsaro, corso una r. corr-/cors-, e confrontarla magari con la radice cour-/cours- delle voci francesi courir, courant, coureur, courrier, course, cours; su un piano diacronico si può risalire alla r. cŭrr- delle voci latine currĕre, currus, curricŭlum ecc., e di qui ricostruire, per mezzo della comparazione con altre lingue indoeuropee, una più antica r. *kers-. Nelle lingue indoeuropee, l’individuazione della r. è spesso complicata dalla presenza dell’apofonia qualitativa e quantitativa (così λειπ-, λοιπ-, λιπ-, grado normale, forte e ‘zero’ della r. individuabile nelle voci greche che esprimono il concetto di lasciare: pres. λείπω «io lascio», perf. λέλοιπα «ho lasciato», aor. ἔλιπον «lasciai»); a volte, inoltre, la r. non è più individuabile, come nel gr. ὤν ὄντος, part. pres. di εἰμί, in cui è cancellata ogni traccia della r. *es-/*s- (εἰμί da ἐσμι, cfr. sanscr. àsmi, lat. esse). Le r. sono individuabili in tutte le lingue flessive e anche in quelle agglutinanti, sebbene meno propriamente, ma non nelle lingue monosillabiche, in cui ogni parola è isolata e autonoma dalle altre.

Matematica

R. n-esima di un numero p reale o complesso

Se n è un intero >1, e p è un numero reale o complesso, si chiama r. n-esima di p ogni numero reale o complesso q, la cui potenza n-esima sia uguale a p e si scrive q=ⁿ√‾‾p. L’operazione che fa passare da un numero p a una sua r. n-esima (estrazione di r.) è quindi l’operazione inversa della elevazione alla n-esima potenza di q; ciò vuol dire che le due relazioni: ⁿ√‾‾p=q; qⁿ=p sono equivalenti. Il numero p si dice radicando, il numero n, indice. Le r. di indice 2, 3, 4, 5, … si dicono anche rispettivamente r. quadrate, r. cubiche, r. quarte (talora r. biquadratiche), r. quinte… Nel caso delle r. quadrate, si usa omettere l’indice e si scrive √‾‾p.

R. aritmetica di un numero reale e positivo

Se p è un numero reale e positivo, esiste uno e un solo numero reale positivo q la cui potenza n-esima è uguale a p. Il numero q si chiama r. n-esima aritmetica di p, o anche, talvolta, r. di p in senso aritmetico. Se a e b sono due numeri reali entrambi positivi, sono inoltre verificate le seguenti relazioni:

Poiché le potenze di esponente pari di un numero negativo sono positive e quelle di esponente dispari sono negative, nel campo dei numeri relativi si presentano i seguenti quattro casi possibili: a) p positivo, n dispari: esiste una r. n-esima reale (e positiva) di p, che è la r. aritmetica q; b) p positivo, n pari: esistono due r. reali n-esime di p, la r. aritmetica q e la sua opposta −q [dato che in tal caso (−q)ⁿ=qⁿ]; c) p negativo, n dispari: esiste una r. n-esima reale q, che è l’opposta della r. n-esima aritmetica dell’opposto di p; per es., l’unica r. cubica reale di −8 è −2; d) p negativo, n pari: non esiste r. n-esima nel campo reale.

Estrazione di r. quadrata

La r. quadrata (e d’ora in poi si sottintenderà aritmetica) di un numero intero positivo, approssimata a meno di una unità, si può calcolare con un procedimento elementare che risale sostanzialmente, salvo l’uso della numerazione sessagesimale, a Teone Alessandrino (4° sec. d.C.). Se il numero ha più di 2 cifre, per es. 88.792, lo si scompone in gruppi di 2 cifre a partire dalla destra, potendo il primo gruppo a sinistra risultare costituito anche da una sola cifra (8.87.92). Il numero dei gruppi così ottenuti dà il numero delle cifre della radice. Si cerca prima il massimo quadrato contenuto nel 1° gruppo di sinistra (8: nel nostro caso tale massimo quadrato è 4): la sua r. (2) è la prima cifra della r. cercata. Si sottrae dal gruppo stesso (8) il quadrato trovato (4), e a destra del resto (8−4=4) si abbassa il 2° gruppo (87). Nel numero risultante (487) si separa la cifra delle unità (7), e si divide il numero rimanente (48), per il doppio (4) della prima cifra già trovata della r. cercata (2). Si scrive il quoziente (o, come nel nostro caso, il numero 9 se il quoziente è maggiore di 9) a destra del doppio (4) della prima cifra già trovata (che era 2), e si moltiplica il numero così formato (49) per il quoziente stesso (o, come nel nostro caso, per 9). Se il prodotto è maggiore del numero costituito dal 1° resto e dal 2° gruppo (487), si deve provare con un quoziente minore, nel caso contrario si fa la differenza (487−441=46), e si prosegue allo stesso modo con i gruppi successivi. I quozienti che man mano si ottengono sono le cifre successive della r. cercata; l’ultimo resto è la differenza tra il numero dato e il quadrato della radice. Si usa disporre l’insieme delle operazioni com’è qui riportato:

Quindi: 88792=297²+583; 297 è la r. quadrata di 88792 a meno di una unità.

Espressione della r. quadrata di un numero a mezzo di una frazione continua

Sia p=a²+s. Posto: x=√‾‾‾‾‾‾a²+s−a‾‾‾ si ricava x²+2ax=s, e quindi x(x+2a)=s; da cui:

Perciò:

Così, per es.:

Le successive ridotte valgono 3/2=1,5; 7/5=1,4;

17/12=1,4166 …; 41/29=1,4137 …;

99/70=1,4142 …; 239/169=1,414201 …

È perciò √‾‾2 = 1,4142 a meno di 1/10⁴.

R. di un numero nel campo complesso

Nel campo complesso un numero

ha n r. n-esime, qualunque sia n. Tali r. hanno per comune modulo la r. n-esima aritmetica di ρ e i loro argomenti sono:

Le loro immagini nel piano complesso sono i vertici di un poligono regolare di n lati. Particolare interesse per il problema della divisione del cerchio in n archi uguali (➔ circonferenza), presentano le r. n-esime dell’unità.

R. n-ma primitiva dell’unità

È ogni r. n-esima che non sia r. dell’unità di indice minore di n: allora le altre r. n-esime sono potenze di essa. Tale è, per es., la r. n-esima che ha per modulo 1 e per argomento 2π/n, cioè il numero complesso ε₁=cos2π /n+i sen2π/n.

R. primitive di un numero primo

Il concetto di r. primitiva si estende dall’aritmetica ordinaria alla teoria delle congruenze (aritmetica in un campo finito). Si dirà in tal caso che un numero a è r. primitiva di un numero primo p quando p–1 è il minimo esponente x per il quale sia: a^x≡1 (mod p). Gauss ha dimostrato che un numero primo ammette sempre r. primitive, indicando al tempo stesso il metodo per il loro calcolo.

R. di un’equazione

Si chiama r. di un’equazione (a una sola incognita) ogni numero (o espressione letterale) che, sostituito all’incognita, muta l’equazione in una identità. Così, per es., i numeri 2 e 3 sono le r. dell’equazione: x²−5x+6=0. Le r. dell’equazione binomia xⁿ=a non sono altro che le r. n-esime di a. In questo caso il significato attuale di r. coincide con il primo significato, e anzi ciò permette di dire che il secondo significato è una estensione del primo.