cilindro

Matematica

fig.

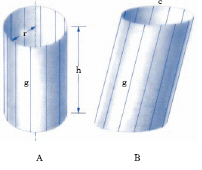
Nella geometria elementare si chiama c. (circolare) indefinito la superficie che si ottiene conducendo per i singoli punti di una data circonferenza di raggio r (direttrice) le perpendicolari al piano della circonferenza (generatrici); il raggio r è detto raggio del cilindro. Evidentemente la stessa superficie si può ottenere facendo ruotare attorno a una retta fissa (asse) la retta (generatrice) a essa parallela a distanza r. Con lo stesso nome di c. si usa designare anche il solido (indefinito) limitato dalla superficie ora detta. Si chiama c. finito (v. fig.) la parte di c. indefinito compresa tra due sezioni piane parallele (tra di loro uguali, dette basi). L’altezza h del c. (finito) è la distanza dei due piani paralleli; il lato, ciascuno dei segmenti, tra di loro uguali, intercettati dalle basi sulle singole generatrici. Se i piani delle due sezioni sono perpendicolari alle generatrici g, le basi sono due cerchi di uguale raggio r, e il c. finito si chiama c. circolare retto (fig. A); se i piani delle due sezioni non sono perpendicolari alle generatrici, le due basi sono ellissi c (caso del c. ellittico obliquo; fig.B).

Nel linguaggio comune, per c. s’intende di solito il c. circolare retto, le cui misure sono: volume = area della base × altezza = πr²∙h; area della superficie laterale = circonferenza di base × altezza = 2πr∙h; nel caso del c. equilatero (h=2r), essa è uguale (Archimede) a quella della superficie della sfera iscritta, 4πr²; area della superficie totale = 2πr(h+r).

Più in generale, prende il nome di c. la superficie luogo delle rette g (generatrici) parallele a una direzione prefissata e passanti per i singoli punti di una data curva C, piana o sghemba (direttrice). Avremo in particolare i c. quadrici se la direttrice è una conica (e a seconda che la direttrice sia un’ellisse, un’iperbole o una parabola si parlerà di c. ellittico, iperbolico o parabolico). Come risulta dalla definizione, i c. sono particolari superfici rigate; anzi sono casi particolari dei coni, potendosi considerare come coni con il vertice all’infinito: come i coni, sono rigate sviluppabili su un piano. Dal punto di vista della geometria analitica l’equazione di un c. è del tipo f(x−az, y−bz)=0, essendo x−az=y−bz=0 le equazioni di una retta parallela alle generatrici, e f una funzione (in particolare un polinomio, per i c. algebrici) dei due argomenti x−az e y−bz. Per z=0 si ottiene l’equazione f(x, y)=0 di una direttrice piana (sul piano z=0).

È detta cilindroide la rigata dotata di una sola direttrice rettilinea impropria: è lo stesso che rigata a piano direttore (le sue generatrici sono tutte parallele a un medesimo piano).

Botanica

C. centrale La regione anatomica del fusto e della radice, detta anche stele, delimitata dal cambio nella struttura secondaria, dal periciclo in quelle primarie. C. corticale La regione anatomica degli stessi organi, detta comunemente corteccia (➔).

Informatica

Insieme delle tracce di un disco magnetico (una per ciascuna superficie magnetizzata) che hanno lo stesso diametro. Tutte le tracce di un disco magnetico possono pertanto pensarsi organizzate in una sequenza di c. coassiali. La lettura e la registrazione dei dati, nell’ambito di uno stesso c., avviene con la sola rotazione del disco senza il movimento radiale del blocco delle testine.

Medicina

Nome di formazioni cilindriche microscopiche che hanno origine nei tubuli renali e si trovano nel sedimento delle urine (cilindruria), in condizioni morbose varie (nefropatie, scompenso di circolo). Sono di varia forma e natura: c. ialini (omogenei con estremità arrotondate e contorni netti); c. granulosi o granulo-grassosi (cosparsi di fini granulazioni e spesso alquanto scuri); c. cerei o colloidi (più rari, omogenei, con orli intagliati da rientranze più o meno profonde); c. epiteliali, c. ematici (ricoperti da epiteli o da globuli bianchi e rossi.

I cilindroidi sono formazioni di sostanza mucoide allungata e ripiegata su sé stessa, più sottili dei c. e che possono trovarsi nel sedimento dell’urina senza alcun significato patologico.

Tecnica

È detto c. l’organo essenziale di molte macchine aventi una superficie di lavoro, interna (ovviamente cava) o esterna, di forma cilindrica (generalmente circolare retta). C. a superficie di lavoro interna sono usati, in particolare, nelle macchine alternative a fluido, sia motrici sia operatrici: la superficie interna di lavoro, cioè la parete del c. sulla quale scorre a tenuta lo stantuffo, è detta camicia o anima, mentre la parte esterna del c. stesso si differenzia in relazione al tipo di macchina. C. a superficie esterna di lavoro (detta mantello del c.) sono usati nelle macchine destinate a lavorazioni meccaniche, come calandre, laminatoi ecc.; il c., in tal caso, può avere superficie liscia o sagomata a seconda dell’impiego e può essere pieno o alleggerito mediante cavità interne.

fig.

Cilindrata È il termine usato per indicare il volume descritto in una corsa semplice dallo stantuffo di una macchina alternativa; se la macchina ha più di un c. la cilindrata si riferisce al complesso degli stantuffi stessi (v. fig.). Si esprime in centimetri cubi, talora in litri, e risulta uguale all’area di uno stantuffo moltiplicata per la corsa e per il numero dei cilindri. Gli autoveicoli e i motoveicoli possono essere classificati in base alla cilindrata dei rispettivi motori: è uno degli elementi per la tassazione del veicolo.