iperbole

Linguistica

Figura retorica, consistente nell’esagerazione di un concetto oltre i termini della verosimiglianza, per eccesso (le grida salivano alle stelle) o per difetto (non ha un briciolo di cervello).

Matematica

In geometria, curva aperta, composta da due parti (rami) staccate e prolungantisi all’infinito, che si ottiene segando un cono circolare con un piano π parallelo a due generatrici di esso (➔ conica). Se, in particolare, π passa per il vertice del cono, si ottiene un’i. degenere costituita da due generatrici del cono.

L’i. è una curva piana del 2° ordine (o conica), rappresentata cioè da un’equazione di 2° grado in x, y (coordinate cartesiane) del tipo:

[1]

per la quale sia:

[2]

fig. 1

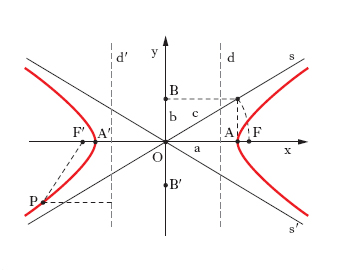
Dal punto di vista geometrico, la disuguaglianza [2] significa che la i. incontra la retta all’infinito in due punti reali e distinti. In parole più semplici: ciascun ramo della curva si prolunga indefinitamente nella direzione di due rette distinte, dette asintoti dell’iperbole. Ciò vuol dire che i due rami si riuniscono nei punti all’infinito dei due asintoti; pertanto l’i., dal punto di vista proiettivo, è una curva chiusa. Il punto di incontro O degli asintoti s, s′ (fig. 1) è centro di simmetria per la curva (centro dell’i.). Le bisettrici degli asintoti (che sono due rette x, y uscenti da O e tra di loro perpendicolari) sono assi di simmetria per la curva (assi dell’i.). L’asse x (detto asse trasverso o principale) incontra l’i. in due punti A, A′ (detti vertici) i quali sono simmetrici rispetto a O, tali cioè che

OA = OA′ = a;

l’altro invece (asse non trasverso o secondario) non taglia l’i. in punti reali. Assumendo le rette x, y come assi coordinati, l’equazione dell’i. si riduce a una forma particolarmente semplice, detta forma canonica:

[3]

(ad a si dà il nome di semiasse trasverso o principale; b si chiama talvolta semiasse non trasverso o secondario e i punti B, B’ ottenuti riportando il segmento b sull’asse y, a partire da O, nei due versi, si dicono estremi di tale asse). Sono notevoli i punti F, F′ dell’asse trasverso simmetrici rispetto a O e aventi da O distanza c=√‾‾‾‾‾‾a²+b²‾‾; essi sono i fuochi dell’i. e la loro costruzione è messa in evidenza in fig.

Si ha, tra l’altro, che: l’i. di equazione [3] è il luogo dei punti tali che la differenza delle loro distanze da F ed F′ (presa in valore assoluto) è uguale alla costante 2a. Le rette d, d′ di equazioni x=a²/c e x=−a²/c si dicono direttrici dell’i.; il rapporto tra la distanza di un punto P dell’i. da un fuoco e la distanza del medesimo punto P dalla direttrice relativa al fuoco prescelto è costante: tale costante è l’eccentricità e=c/a>1 dell’iperbole. L’una e l’altra proprietà offrono le consuete definizioni elementari dell’iperbole e ne giustificano l’equazione polare che è del tutto analoga a quella dell’ellisse e della parabola.

Si chiama equilatera un’i. nella quale gli asintoti sono tra loro ortogonali ( fig. 1), il che porta di conseguenza l’uguaglianza dei semiassi a e b («lati», donde il nome).

fig. 2

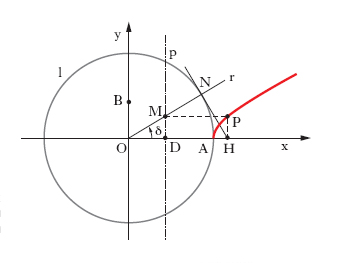
Per costruire un’i. (fig. 2), quando siano dati i semiassi a e b, si traccino sul piano Oxy i segmenti DA=a e OB=b (sugli assi x e y rispettivamente) e la circonferenza l di centro O e raggio a. Si riporti sull’asse x il segmento OD=b e per D la parallela p a OB; sia r una semiretta variabile per O, siano M, N i punti di incontro di r con p e l rispettivamente; la tangente in N alla l intersechi l’asse x in H; la parallela per H alla OB e la parallela per M alla OA si intersecano in un punto P, che, al variare di r, descrive l’i.; la giustificazione della costruzione si ottiene osservando che, posto AON=δ, le coordinate x, y di P soddisfano alle relazioni x/a=1/cosδ, y/b=tgδ (equazioni parametriche dell’i.), le quali, per eliminazione del parametro δ, forniscono la [3].