indice

In senso generico ed etimologico, da cui si sviluppano tutti i significati particolari, qualsiasi cosa che serve a indicare.

Anatomia

Dito i. È il secondo dito della mano, tra il pollice e il medio: ha una notevole importanza, sia per l’autonomia dei movimenti rispetto alle altre dita, sia perché partecipa alla prensione ‘a pinza’, ‘ad anello’, ‘a uncino’. I movimenti dell’i. sono regolati da muscoli flessori ed estensori (flessore superficiale e profondo delle dita; estensore comune delle dita; estensore proprio dell’indice).

Astronomia

I. di colore Numero che esprime la differenza delle grandezze di un astro determinate in due diverse regioni o colori dello spettro. Generalmente è detto i. di colore la differenza tra la grandezza visuale (corrispondente al giallo, colore per il quale l’occhio ha la massima sensibilità) e quella fotografica (corrispondente al violetto, per il quale è massima la sensibilità delle lastre fotografiche); esso misura sostanzialmente il colore dell’astro e, essendo questo strettamente collegato, a norma della legge di Wien (➔ Wien, Wilhelm), con la temperatura e quindi con il tipo spettrale, esso dà un’indicazione sintetica delle sue più importanti caratteristiche fisiche.

I. di rifrazione assoluto (di fase) di un mezzo Per una certa radiazione monocromatica, il rapporto fra la velocità della luce nel vuoto e la velocità di fase di quella radiazione nel mezzo considerato. Per mezzi dielettrici non ferro- né ferrimagnetici è pari alla radice quadrata della costante dielettrica relativa. Varia con la frequenza della radiazione (fenomeno della dispersione). I. di rifrazione assoluto di un mezzo Per una certa radiazione non monocromatica, il rapporto fra la velocità della luce nel vuoto e la velocità di gruppo di quella radiazione nel mezzo considerato (➔ rifrazione).

Ecologia

In ecologia vegetale, gli i. sono scale ordinali impiegate per quantificare, mediante una stima, un fattore ecologico in grado di determinare la sopravvivenza di una data specie. Particolarmente noti sono gli i. di Ellenberg, detti anche valori di bioindicazione (➔ Ellenberg, Heinz), che correlano una data specie alle sue preferenze ecologiche ed edafiche. Altri i. sono quelli proposti dalla IUCN per quantificare la vulnerabilità di una data specie in funzione delle minacce incombenti e dell’entità numerica delle popolazioni esistenti.

Economia

In economia aziendale, i. di bilancio sono utilizzati per valutare le condizioni strutturali e funzionali dell’azienda sul piano patrimoniale, finanziario ed economico. Tra questi, i più importanti sono gli i. di redditività (che mettono l’utile dell’azienda in relazione al capitale impiegato, al capitale proprio o al fatturato), l’i. di indebitamento (riferito alla struttura dell’indebitamento nell’impresa), l’i. di produttività (che mette a confronto i beni prodotti e i fattori di produzione impiegati), l’i. di rotazione dei crediti o debiti commerciali, dei magazzini o del capitale investito (per valutare la loro durata media) ecc.

Nel linguaggio finanziario, il numero i. del costo della vita misura le variazioni dei prezzi delle merci e dei servizi di largo consumo, nei bilanci delle famiglie di operai e impiegati. I. di borsa (o azionari) sono gli i. che riguardano l’andamento del mercato preso in esame; sono calcolati prendendo come base le variazioni dei prezzi di tutti o di un certo numero di titoli. I principali indici delle borse italiane sono il MIB e il MIBTEL.

Informatica

Tavola di riferimento ordinata in base a opportuni indicativi e registrata nella memoria di un calcolatore, che può essere consultata per trovarvi gli indirizzi di certi dati contenuti nella memoria.

Linguistica

In lessicografia e in linguistica computazionale, lista delle parole presenti in un testo sottoposto a spoglio lessicale, ordinate alfabeticamente o in base alla frequenza delle occorrenze.

Matematica

Nella teoria dei numeri interi si chiama i. di un numero a, alla base g, rispetto a un modulo primo dispari p, il numero intero m, compreso tra 0 e p-2, sempre esistente e unico, per il quale si ha: g^m≡a (mod. p), per il quale cioè g^m−a è divisibile per p; l’i. di a si indica col simbolo inda. Per es. l’i. di 2 alla base 3 rispetto al modulo 5 è m=3, in quanto: 3³−2=25 è divisibile per 5. Le regole di calcolo per gli i. ricordano, come è anche naturale data la definizione, le regole fondamentali dei logaritmi; per es. ind(ab)=inda+indb; indaⁿ=n inda.

I. di un radicale è il numero che si scrive sopra il segno di radice e rappresenta l’esponente a cui va elevato il radicale per ottenere il radicando. Nel caso della radice quadrata l’indice non è scritto. I. di allacciamento di due curve nello spazio ordinario è un numero che indica come esse sono concatenate; se una delle due curve è chiusa, esso è dato dal numero minimo dei punti di incontro della seconda con una porzione di superficie avente per bordo la prima.

Sono detti i. anche numeri legati a operatori differenziali. Per es., l’i. analitico i_a di un operatore differenziale lineare F tra due spazi vettoriali V e U è definito da: i_a(F)=dim KerF−dim CokerF, essendo Ker il nucleo di F, Coker l’insieme quoziente dello spazio di arrivo U rispetto all’immagine di F e dim la dimensione del sottospazio. L’i. topologico i_t è invece definito dalle caratteristiche topologiche degli spazi su cui l’operatore è definito.

In statistica, mediante i. è possibile avere un’idea sintetica del modo di essere o di comportarsi di un dato fenomeno nel tempo e nello spazio o anche della relazione intercorrente tra più fenomeni: ciascun i. assume, di regola, una denominazione specifica in relazione a ciò che vuole esprimere o al procedimento impiegato per il calcolo; così si ha l’i. di contingenza, di dissomiglianza, di evoluzione, di oscillazione, di natalità ecc. Particolare significato hanno alcuni i., quali, per es., l’i. a di Pareto, l’i. d di Gini, l’i. t di Student, l’i. di Tait.

Numeri i. Numeri che esprimono l’entità attuale di un dato statistico (costo di una merce, consumo di un prodotto ecc.) rispetto a quella di un’epoca di riferimento, che viene di norma posta uguale a 100. I numeri i. si distinguono in semplici o elementari se riferiti all’entità attuale di un dato statistico elementare (per es., il prezzo di una merce), e composti o sintetici se riferiti all’entità attuale di un fenomeno composto di più elementi quantitativi elementari (per es., numero i. dei prezzi dei prodotti alimentari).

Tecnica

fig. A

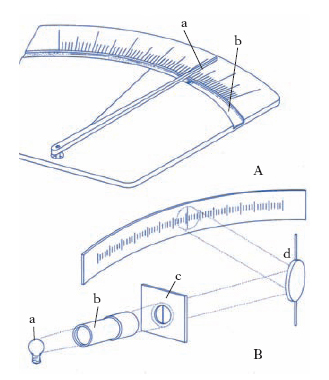
L’indice di uno strumento analogico è una asticella libera di ruotare intorno a un asse fisso e il cui moto è provocato, direttamente o indirettamente, dalla grandezza da misurare: l’estremità dell’i. si muove su una scala graduata e, una volta tarato l’apparecchio, essa indica il valore della grandezza. Per strumenti di precisione l’i. deve essere molto sottile in corrispondenza della scala graduata, al fine di poter apprezzare con sufficiente esattezza le frazioni di graduazione della scala stessa; dovrà essere inoltre molto vicino alla scala, così da poter considerare trascurabile l’errore di parallasse (fig. A). Nel caso di piccole deviazioni angolari dell’equipaggio mobile dello strumento, conviene sostituire all’i. meccanico un i. fittizio costituito da un pennello di raggi luminosi (i. ottico; fig. B), che può farsi, entro certi limiti, lungo a piacere, sfruttando il principio amplificatore della leva ottica (➔ leva).