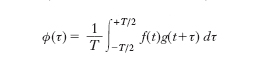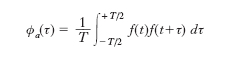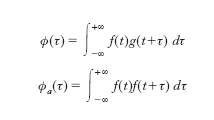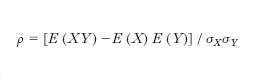correlazione

Stretta corrispondenza fra due (o anche tra più) elementi.

Biologia

La c. fra gli organi si attua attraverso la c. chimica (o umorale) e la c. nervosa. La prima avviene per mezzo di sostanze elaborate da un organo, per es., gli organizzatori dello sviluppo inducono determinati processi morfogenetici nei territori con cui sono a contatto. Nell’adulto le c. umorali sono dovute agli ormoni elaborati dalle ghiandole endocrine. Le c. nervose, durante lo sviluppo, guidano i processi morfogenetici, e nell’adulto stimolano o inibiscono la funzionalità di vari organi, o determinano reazioni motorie.

In neurologia, la c. è la combinazione di impulsi centripeti che avviene nei centri sensoriali spinali o encefalici.

Matematica

Date due funzioni periodiche f (t), g (t) di uguale periodo T, si chiama funzione di c. (o di c. incrociata o, all’ingl., cross-c.) la funzione

Se f (t) = g (t), si ha

che prende il nome di funzione di autocorrelazione; per τ = 0 la funzione di autocorrelazione φa (0) è uguale al valore quadratico medio della f (t). Queste definizioni valide per le funzioni periodiche, possono essere estese alle funzioni non periodiche:

Statistica

Tra due variabili empiriche esiste c. quando si constata la tendenza di una di esse a variare con un’approssimazione più o meno grande (con un grado di c. più o meno alto) in funzione dell’altra. Così, per es., si dice che esiste una c. tra la statura del figlio (adulto) e quella del padre, perché, passando dalle stature più basse alle più alte dei padri, le stature dei figli, in media, tendono a crescere. La più stretta c. pensabile tra due variabili empiriche si avrebbe se a un valore dell’una corrispondesse un ben determinato valore dell’altra; cioè se la seconda fosse una funzione a un sol valore della prima, anzi una funzione lineare. L’assenza di c. si ha invece quando a ogni valore della prima corrisponde la stessa distribuzione di valori dell’altra. Si parla di c. diretta (o positiva) o di concordanza di variazioni, se al crescere della variabile indipendente anche quella dipendente tende a crescere; di c. inversa (o negativa) o di discordanza di variazioni nel caso opposto (all’aumentare dell’una, l’altra tende a decrescere). Il grado di c. si può, in certo modo, misurare sulla base dei dati statistici mediante un coefficiente (o indice) di c., che viene definito in modo da risultare uguale a 1 nel caso della dipendenza lineare accompagnata da concordanza, uguale a 0 nel caso di mancanza di c., e a –1 nel caso di dipendenza lineare accompagnata da discordanza. Più precisamente, il coefficiente di c. tra le variabili X e Y è definito da

,

dove con E e σ² si indicano rispettivamente il valore atteso e la varianza (➔ probabilità). Per n variabili X1 , ..., Xn , si chiama matrice di c. la matrice quadrata di ordine n il cui elemento generico ρij è il coefficiente di c. tra Xi e Xj. Si tratta di una matrice simmetrica, che ha gli elementi della diagonale principale uguali a uno. Si chiama poi tabella di c. la tabella a doppia entrata che riporta le frequenze di una serie di dati, classificati rispetto a due caratteri.