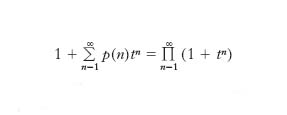partizione

Araldica

Le p. sono divisioni dello scudo mediante una o più linee orizzontali, verticali, diagonali o per mezzo di linee convergenti, al fine di creare campi diversi per accogliere stemmi o figure a seguito di alleanze matrimoniali, successioni ereditarie, concessioni e pretensioni di domini, o maggiorascati ecc. (armi di alleanza, di possesso, di concessione, di pretensione). Alcune p. si possono riferire sia al campo che alle figure. Per blasonare le p. (➔ blasonatura) è necessario visualizzare lo scudo come se fosse indossato dal cavaliere per cui la parte destra corrisponderà alla sinistra di chi guarda e viceversa. Le p. si definiscono semplici quando sono tracciate da una sola linea, composte (dette anche ripartizioni) quando sono tracciate da due o più linee, straordinarie se sono definite da linee che seguono direzioni diverse.

Le p. semplici

fig.

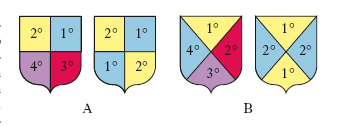
L’origine delle p. semplici si fa risalire alle spaccature procurate dalle armi da taglio sugli scudi dei cavalieri in battaglia. Esse sono: il partito, il troncato, il trinciato, il tagliato, l’addestrato e il sinistrato (v. fig.).

Partito è lo scudo diviso in due parti uguali da una linea verticale che passa per il centro. Troncato (o spaccato) è lo scudo diviso in due parti uguali da una linea orizzontale.

Trinciato è lo scudo diviso in due parti uguali da una linea diagonale che parte dall’angolo superiore destro fino al sinistro.

Tagliato è lo scudo diviso in due parti uguali da una linea diagonale che parte dall’angolo superiore sinistro fino al destro.

Addestrato è lo scudo diviso in due parti non uguali da una linea verticale che non passa per il centro ma è spostata a un terzo della larghezza dello scudo, verso destra.

Sinistrato è lo scudo diviso in due parti non uguali da una linea verticale che non passa per il centro ma è spostata a un terzo della larghezza dello scudo, verso sinistra.

Le p. composte o ripartizioni

Molto numerose, le principali p. composte sono: l’interzato, l’inquartato, il controinquartato, lo spaccato-semipartito, il semipartito-spaccato, il partito-semispaccato, il semispaccato-partito.

Interzato è lo scudo diviso in 3 parti uguali da 2 linee parallele verticali o orizzontali o diagonali (da destra a sinistra o da sinistra a destra) nel qual caso viene definito interzato in palo, in fascia, in banda, in sbarra.

Inquartato è lo scudo diviso in 4 parti uguali (che sono chiamati quarti) da una linea verticale e una orizzontale che si incontrano al centro; se le linee che si intersecano sono diagonali si chiama inquartato in decusse o in croce di s. Andrea.

Controinquartato è lo scudo in cui uno dei quarti o tutti i 4 quarti sono nuovamente inquartati.

Spaccato-semipartito è lo scudo spaccato e partito nella parte inferiore.

Semipartito-spaccato è lo scudo spaccato e partito nella parte superiore.

Partito-semispaccato è lo scudo partito e spaccato nella parte sinistra.

Semispaccato-partito è lo scudo partito e spaccato nella parte destra.

Altre p. sono composte dall’incrocio di più linee verticali e orizzontali che dividono lo scudo in numerosi quarti come per es.: partito di uno e troncato di due (che forma 6 quarti), partito di due e troncato di due (9 quarti), partito di due e troncato di tre (12 quarti). Si può arrivare fino a partito di cinque e spaccato di sette che divide lo scudo in 48 quarti. Comunque in Italia le p. più complesse non sono frequenti.

Le p. straordinarie

Formate da linee che prendono direzioni diverse, le p. straordinarie sono molto rare nell’araldica italiana.

Semispaccato, semipartito verso la punta e rispaccato: lo scudo è spaccato in capo, partito verso la punta e nuovamente spaccato in punta; semipartito, semitagliato e ripartito: lo scudo è partito in capo, tagliato verso il capo o verso la punta e nuovamente partito in punta; semitrinciato-semitagliato e ritrinciato: lo scudo è trinciato in capo, tagliato verso il canton sinistro del capo o verso il canton destro della punta e trinciato nella punta; semitagliato-semispaccato e ritagliato: lo scudo è tagliato in capo, spaccato verso destra o verso sinistra e nuovamente tagliato in punta; interzato in pergola e in pergola rovesciata: lo scudo è diviso in 3 parti da una semiretta che al centro si divide in due semirette che toccano gli angoli superiori oppure inferiori; interzato in calza: lo scudo è diviso in 3 parti da 2 linee diagonali che partono dagli angoli superiori e convergono nella punta; interzato in mantello: lo scudo è diviso in 3 parti da 2 linee diagonali che partono dagli angoli inferiori e convergono nel capo; interzato incappato: lo scudo è diviso in 3 parti da 2 linee curve che partono dal centro e raggiungono i fianchi dello scudo; interzato in grembi ritondati: lo scudo è diviso in 3 parti da 3 linee curve. Per descrivere questo tipo di p. occorre osservare in che modo queste linee dividono il campo e a quali p. semplici somigliano separatamente.

Esistono inoltre le convenevoli p.: si costituiscono quando le pezze araldiche (➔ pezze) si ripetono sullo scudo coprendolo per intero e dividendolo in due smalti diversi; le principali sono: il fasciato, il palato, il bandato, lo sbarrato, il fusato, il losangato, lo scaccato ecc., e le p. delle riduzioni ossia convenevoli p. costituite da pezze araldiche ridotte come il burellato, il cotissato, il traversato.

Caratteristiche

Le linee di contorno delle p., ma anche quelle che delimitano le pezze, non sono necessariamente dritte ma possono presentarsi di forme molteplici: merlate, con i merli da un solo lato, doppiomerlate con i merli da ambo i lati, controdoppiomerlate con merli opposti da ambo i lati, merlate alla ghibellina con i merli intaccati superiormente a taglio triangolare, nebulose a forma di onde grosse o nuvole, inchiavate con denti lunghi e triangolari, dentate con piccoli denti, scanalate con i denti in dentro e i dossi di fuori, spinate con piccoli denti che si arrotondano ai lati, ondate con onde. Queste linee diventano attributi delle partizioni e verranno blasonate, per es., come partito merlato, spaccato nebuloso, trinciato inchiavato ecc.

Matematica

Nella teoria degli insiemi si chiama p. in classi di un insieme E ogni famiglia {A_i}_i∈I di sottoinsiemi di E a due a due disgiunti e aventi E come unione. Considerate due p. di uno stesso insieme E può accadere che ognuno dei sottoinsiemi di E costituenti la prima p. contenga un sottoinsieme della seconda: in tal caso si dice che la seconda p. è ‘più fina’ della prima (o che è un raffinamento della prima) o che la prima è ‘meno fina’ o più grossolana della seconda; la p. più fina di tutte è ovviamente quella che ha come elementi i singoli elementi di E mentre la più grossolana è quella che ha un unico elemento e cioè lo stesso E. A ogni p. in classi {A_i} di un insieme E si può associare una ben determinata relazione di equivalenza R su E: precisamente due elementi x, y di E si dichiarano equivalenti se appartengono a uno stesso elemento A_i della partizione. In altre parole le classi della p. sono assunte a classi di equivalenza di R. Viceversa ogni relazione di equivalenza in un insieme E dà luogo a una p. di E. P. di un numero naturale n È un caso particolare di p. di un insieme: l’insieme è ora costituito da tanti elementi quante sono le unità di n. Si tratta, cioè, di esprimere il numero n come somma di numeri interi positivi, detti anche parti, e valutarne il numero di modi. Se gli addendi della somma si considerano tenendo conto dell’ordine, il numero delle p. di n, che si indica di solito con p(n) o π(n), è 2ⁿ⁻¹. Se gli addendi si considerano prescindendo dall’ordine, le p. coincidono con i coefficienti di serie esponenziali, dette anche funzioni generatrici della successione delle partizioni. Così, dette p(n) le p. di n con parti non ripetute e p′(n) le p. di n con parti costituite da numeri dispari, eventualmente ripetuti, si ha

ed è stato dimostrato da L. Euler che p(n) = p′(n). Per es., le p. di 9 in cui figurano solo addendi diversi sono 8 e precisamente: 9 = 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5 = 1 + 2 + 6 = 1 + 3 + 5 = 2 + 3 + 4.

P. dell’unità In geometria differenziabile, è una tecnica di grande utilità nelle questioni attinenti all’integrazione sulle varietà differenziabili. Limitandosi ai fatti essenziali, si può dire che se una varietà differenziale V è paracompatta, comunque si assegni un ricoprimento {U_i}_i∈I di V è possibile individuare una famiglia {f_i}_i∈I di funzioni definite in V, una per ogni aperto del ricoprimento (tutte continue e anzi aventi una certa classe di differenziabilità), tali che ciascuna di esse sia zero al di fuori del corrispondente intorno del ricoprimento, e inoltre in ogni punto di V solo un numero finito di esse abbia valore diverso da zero e infine la somma di tali valori sia sempre uguale a 1. In certo senso, cioè, la funzione definita su V e uguale costantemente a 1 (funzione unità) si può ottenere, in ogni punto di V, come somma di un numero finito di funzioni f_i (variabili però, naturalmente, da punto a punto): per questa ragione la famiglia {f_i} si chiama p. dell’unità subordinata al ricoprimento {U_i} di V e il classico teorema che ne garantisce l’esistenza è detto appunto teorema della p. dell’unità.