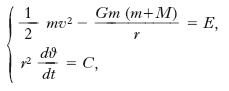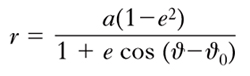orbita

Anatomia

Ciascuna delle due cavità dello scheletro della testa, separate tra loro dalle fosse nasali, che contengono i globi oculari con i loro principali annessi. L’insieme dell’o. e delle parti molli in essa contenute o che la rivestono (palpebre) costituisce la regione orbitale.

Le o. sono situate simmetricamente su ciascun lato della linea mediana, a una distanza di circa 25 mm. Hanno approssimativamente forma di piramide quadrangolare, con la base in avanti (detta anche apertura orbitale, perché aperta all’esterno) e l’apice indietro. Alla costituzione delle pareti dell’o. (superiore, inferiore, laterale e mediale) partecipano varie ossa: il frontale, lo sfenoide, l’etmoide, il lacrimale, il palatino, il mascellare superiore, lo zigomatico. Posteriormente l’o. comunica con la cavità cranica mediante il foro ottico (passaggio del nervo ottico ecc.) e la fessura sferoidale (passaggio di varie formazioni, tra cui terzo, quarto, sesto e prima branca del quinto paio di nervi cranici). Nella stessa fessura è compresa una formazione anulare (anello di Zinn) su cui si inseriscono i quattro muscoli retti dell’occhio e il muscolo grande obliquo. L’o. contiene inoltre il piccolo obliquo, il muscolo elevatore della palpebra superiore, il ganglio ciliare con le sue radici e le sue branche, i rami dell’arteria oftalmica, le vene oftalmiche, la ghiandola lacrimale ecc. Gli spazi tra le diverse formazioni anatomiche sono colmati da una massa di tessuto cellulare (corpo adiposo dell’o.). L’indice orbitale (o orbitario) è la misura craniometrica espressa dal rapporto fra l’altezza e la larghezza dell’apertura dell’o., moltiplicato per 100.

Il lobo orbitale costituisce la faccia inferiore, o basale del lobo frontale del cervello, che poggia sulla volta dell’orbita.

L’orbitonometria è la misura della tensione del globo oculare, che può essere eseguita approssimativamente mediante la palpazione, o con grande precisione utilizzando un orbitonometro.

L’orbitotomia è l’intervento chirurgico di apertura della cavità orbitaria con un’incisione delle parti molli, generalmente curvilinea sul bordo orbitario, al fine di asportare cisti, tumori, o formazioni patologiche intraorbitarie.

Astronomia e astronautica

Traiettoria descritta dal moto di un corpo in movimento intorno a un altro corpo; il termine è particolarmente usato per indicare la traiettoria di un corpo animato da moto centrale, e quindi in astronomia con riferimento al moto dei pianeti intorno al Sole e dei satelliti intorno a un pianeta e in astronautica con riferimento al moto di satelliti artificiali terrestri e di veicoli spaziali in genere.

Per l’uso del termine in fisica atomica, con riferimento al moto degli elettroni di un atomo attorno al nucleo, secondo il modello atomico di Bohr, ➔ atomo.

Teoria delle orbite

A Keplero è dovuta la precisazione della dinamica delle o. planetarie, condensate nelle tre celebri leggi del moto dei pianeti: le o. dei pianeti sono ellissi di cui il Sole, S, occupa uno dei fuochi (1609); i raggi vettori, r, che uniscono i pianeti al Sole descrivono aree uguali in tempi uguali (1609); i quadrati dei periodi di rivoluzione sono proporzionali ai cubi dei semiassi maggiori, a, delle orbite (1619). I. Newton, formulati i principi della dinamica, interpretò in base a essi le leggi di Keplero, deducendo che il Sole esercita su un pianeta una forza centrale proporzionale alla massa del pianeta e inversamente proporzionale al quadrato della distanza del pianeta dal Sole. Newton dedusse poi che tale forza non si limita al Sole e ai pianeti e che due corpi puntiformi qualsiasi si attirano reciprocamente con una forza proporzionale al prodotto delle masse m₁, m₂ e inversamente proporzionale al quadrato della loro distanza r, secondo la legge della gravitazione universale:

,

con G costante della gravitazione universale. Inversamente, lo studio del moto di due punti materiali isolati nello spazio e sottoposti pertanto solo alla reciproca attrazione newtoniana riconduce come caso particolare al moto ellittico descritto dalle leggi di Keplero. Il problema, se i due corpi hanno massa tra loro confrontabile, si risolve studiando il movimento dei due corpi intorno al comune centro di massa. Se uno dei due corpi ha massa molto maggiore dell’altro, come nel caso del Sole S e di un pianeta T, il problema si risolve studiando il moto di T intorno a S e ponendo in S la massa totale del sistema, somma della massa M del Sole e della massa m del pianeta. L’equazione del moto di T è in questo caso:

[1] formula,

dove r è il raggio vettore che congiunge S a T. Essendo la forza che agisce su T sempre diretta verso S, il momento della quantità di moto si conserva e quindi il moto si svolge in un piano. Per individuare la forma o l’orientamento dell’o. sul piano del moto si risolve il sistema costituito dalle equazioni che esprimono la conservazione dell’energia meccanica totale E e del modulo del momento della quantità di moto:

[2] formula,

essendo C il doppio della velocità areale in coordinate polari, con polo in S. Esprimendo anche la velocità v in coordinate polari si ottiene:

[3] formula,

avendo posto

[4] formula,

tab.

fig. 1

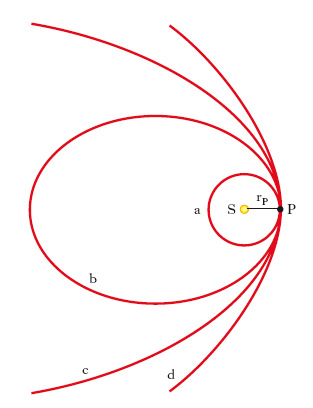
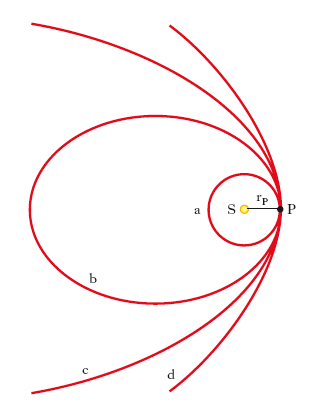
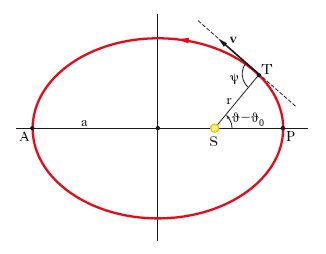
la [3] è l’equazione polare di una conica con fuoco in S, asse inclinato di ϑ₀ sull’asse scelto come asse di riferimento delle coordinate polari, parametro p ed eccentricità e. Si può concludere pertanto che il moto di un corpo sottoposto a una forza attrattiva centrale, inversamente proporzionale al quadrato della distanza dal centro di attrazione, è piano e che l’o. è sempre una conica con un fuoco nel centro della forza. Tale conica è un’ellisse (caso kepleriano), una parabola o un’iperbole a seconda che sia, rispettivamente, e Ü 1 cioè E Ü 0. In virtù della prima equazione del sistema [2], tali condizioni in termini di energia meccanica totale E sono equivalenti a condizioni in termini di velocità v e di distan;za r dal centro S del moto (v. tab. e fig. 1).

Nel caso del moto dei pianeti intorno al Sole, cioè nel caso di un’orbita ellittica, sostituendo a p il valore a(1−e²) dato dalla geometria analitica, la [3] assume la forma (nota come equazione di Keplero)

fig. 2

essendo a il semiasse maggiore dell’o., la cui eccentricità e è minore dell’unità. Se si indica con A l’afelio, con P il perielio (fig. 2), è chiaro che a T in P corrisponde ϑ=ϑ₀ [r assume il minimo valore, la distanza al perielio, r_P=a(1−e)], mentre a T in A corrisponde ϑ=ϑ₀+π [r assume il massimo valore, la distanza all’afelio, r_A=a(1+e)]. Combinando la seconda delle [2] con la [4], si ottiene: G(M+m)=α²a³, dove α è la velocità angolare media, che è la cosiddetta equazione fondamentale della teoria delle o. (in sostanza, è la 3ª legge di Keplero). Nel caso di o. paraboliche e iperboliche, si perviene, analogamente, a equazioni, che, come quella di Keplero, ammettono soluzione unica.

Velocità orbitale

La direzione e l’orientamento della velocità v sono quelli della tangente all’o. nella posizione di T, orientata nel verso del moto (fig. 2). Quanto al valore della velocità, combinando la prima delle [2] con la [4], si ricava:

[5] formula.

Si vede dunque che, variando r lungo l’o., v non è costante; precisamente, è massima quando r è minima, cioè al perielio, e minima quando r è massima, cioè all’afelio. In particolare, se l’o. è circolare (r=a), la velocità è costante, e vale:

se l’o. è parabolica (e=1), si ha, essendo a infinitamente grande,

[6] formula;

ne segue che la velocità di un astro su un’o. parabolica (è il caso di varie comete) diminuisce via via che aumenta la distanza dal Sole. La velocità data dalla [6] è detta anche velocità di fuga, o di liberazione, in quanto per velocità superiori a essa si hanno o. iperboliche (v. tab.), cui corrisponde l’indefinito allontanamento dell’astro dal Sole.

Elementi di un’orbita

fig. 3

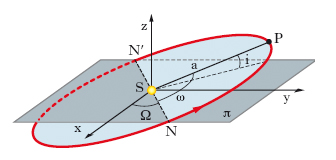
L’equazione vettoriale [1], che è alla base della teoria delle o., è traducibile in un sistema di tre equazioni differenziali scalari del secondo ordine: ciò significa che nella soluzione intervengono 6 costanti d’integrazione. La scelta dei 6 parametri necessari e sufficienti per individuare un’o. e la posizione su essa del corpo orbitante, può essere fatta in vari modi. La via che normalmente si segue è la seguente. Si conviene di riferire la giacitura dell’o. al piano π dell’eclittica (fig. 3) a una certa epoca, per es., alla mezzanotte del 1° gennaio 1900; viene introdotta una terna cartesiana di riferimento, con origine nel Sole S, asse x diretto verso il punto vernale (intersezione, sulla sfera celeste, dell’eclittica con l’equatore all’equinozio di primavera), asse z diretto verso l’emisfero celeste contenente il polo celeste Nord. Chiamato nodo ascendente dell’o. il punto N in cui l’o. taglia il piano dell’eclittica in corrispondenza al passaggio da valori negativi a valori positivi della coordinata z (l’altro punto N′ di intersezione è il nodo discendente), un primo elemento è la longitudine del nodo, cioè l’angolo Ω che la linea dei nodi, N′N, forma con l’asse x, contato, come ogni altro angolo, nel verso diretto, vale a dire nel verso antiorario. Un secondo elemento, che insieme con il precedente individua la giacitura del piano dell’o., è l’inclinazione, cioè l’angolo diedro i che ha per spigolo la linea dei nodi e per facce la parte del piano dell’o. per cui si hanno coordinate z positive e la parte del piano dell’eclittica per cui si hanno coordinate y positive. Per o. dirette (come accade per tutti i pianeti) i è minore di 90°, mentre per o. retrograde (come accade per varie comete) i è maggiore di 90° (per es., per la cometa di Halley, si ha i=162°); così, i informa immediatamente, con il suo valore, se l’o. è diretta o retrograda. Un terzo elemento, che individua l’orientamento dell’asse maggiore dell’o., è la distanza del perielio dal nodo, cioè l’angolo ω che SN, congiungente il Sole con il nodo, forma con SP, congiungente il Sole con il perielio P. Per precisare la forma dell’o. bastano poi il semiasse maggiore a (usualmente espresso in unità astronomiche) e l’eccentricità e; infine, come sesto e ultimo elemento, essendo l’o. completamente determinata dai precedenti 5 elementi, si assume l’istante del passaggio al perielio, cioè l’istante al quale T occupa una ben determinata posizione.

L’o. in astronautica

Nei suoi termini generali, il problema della determinazione dell’o. di un veicolo lanciato nello spazio circumterrestre per divenire un satellite artificiale della Terra oppure lanciato nello spazio interplanetario per raggiungere la Luna o un pianeta, è risolubile nel quadro della teoria delle o. astronomiche. Particolarmente rilevanti al riguardo sono le considerazioni che in astronomia si fanno sull’importanza del valore e della direzione della velocità iniziale (velocità di lancio) nei riguardi del tipo di orbita. Per quanto riguarda i satelliti artificiali terrestri e più in generale i veicoli spaziali, gli elementi che sono correntemente dati per l’o. sono la quota al perigeo, la quota all’apogeo e l’inclinazione del piano dell’o. sul piano dell’equatore terrestre (per inclinazione pari a 90° si hanno o. polari, per inclinazione nulla si hanno o. equatoriali); tra le varie espressioni in uso per indicare tipi particolari di o. circumterrestri vanno menzionate l’o. geostazionaria (o stazionaria), che indica un’o., pressoché circolare, percorsa con la stessa velocità angolare del moto di rotazione terrestre e nel verso di questo, per modo che il satellite appare in quiete sulla verticale di un certo luogo della Terra, e l’o. di parcheggio, che indica un’o. circumterrestre da cui il veicolo successivamente si stacca per dirigersi verso altri astri oppure per ritornare a terra. Va osservato che le o. di satelliti artificiali terrestri risultano sempre fortemente perturbate, soprattutto per effetto del frenamento a opera dell’atmosfera superiore e per effetto della non sfericità e non omogeneità della Terra; da questo punto di vista lo studio delle loro perturbazioni, effettuato rilevando con continuità gli elementi orbitali (soprattutto con metodi radioelettrici), si è rivelato un potente mezzo per indagare sulla densità atmosferica nonché sulla forma della Terra e sulla distribuzione della massa in essa. Ancora più complesso si presenta poi il caso dell’o. di veicoli lanciati nello spazio interplanetario; in genere, ai calcoli preliminari, che peraltro si cerca di condurre nel modo più preciso possibile, si dà carattere di approccio, riservandosi poi di effettuare appropriate correzioni di o., mediante l’azionamento radiocomandato di motori direzionali del veicolo, nel caso che l’o. effettiva risultasse diversa da quella che il veicolo deve seguire.