gravitazione

Proprietà fondamentale e caratteristica (insieme con l’inerzia) di tutta la materia consistente nel fatto che fra due corpi materiali si esercita sempre una mutua attrazione, direttamente proporzionale alle loro masse e inversamente proporzionale al quadrato della loro distanza. La forza di g. tra due masse puntiformi m e M, poste a distanza r l’una dall’altra, è diretta secondo la loro congiungente e vale

,

dove G è una costante (costante di g. universale, o di Cavendish) il cui valore, nel sistema internazionale, è:

G=(6,67428±0,00067) 10⁻¹¹ m³kg⁻¹s⁻².

La massa viene detta massa gravitazionale quando si vuole porre l’accento sul fatto che la massa di un corpo determina l’intensità del campo di attrazione gravitazionale generato nello spazio circostante dal corpo stesso.

La legge di g. universale

La legge di g. universale, la cui scoperta è dovuta a I. Newton (1687), dà ragione del moto dei pianeti intorno al Sole e dei satelliti intorno ai pianeti, della caduta dei gravi sulla superficie della Terra ecc., e costituisce pertanto la base di tutta la di;namica cosmica. Numerose osservazioni astronomiche hanno sostanzialmente confermato la validità della legge di Newton: fra esse celebre la scoperta del pianeta Nettuno (1846) nel punto esatto del cielo teoricamente previsto da U. Leverrier in base allo studio delle anomalie nel moto di Urano. Tuttavia alcune altre anomalie (per es., lo spostamento del perielio dei pianeti e la recessione delle nebulose extragalattiche) non si spiegano con la teoria classica. Così, difficoltà di natura teorica e contrastanti risultati sperimentali hanno suggerito varie modifiche alla legge di Newton (P.-S. Laplace, H.A. Lorentz ecc.) e dato vita a nuove teorie, tra le quali segnano una svolta di fondamentale importanza quelle dovute ad A. Einstein.

La teoria gravitazionale di Einstein, nell’ambito della teoria della relatività generale (1915), interpreta gli effetti della g. come dovuti alla variazione delle proprietà geometriche dello spazio. La presenza di una massa altera la metrica dello spazio circostante; questa alterazione si manifesta, per es., con il fatto che in prossimità di una massa le geodetiche non sono linee rette. La teoria relativistica della g. prende le mosse dal principio di equivalenza di Einstein che può essere generalizzato nella forma: per ogni elemento infinitesimo dello spazio-tempo esiste sempre un sistema di riferimento K₀ (X₁, X₂, X₃, X₄) nel quale localmente non si risentono in modo alcuno gli effetti della gravità; il sistema K₀ può venire concettualmente realizzato con una piccola scatola che cada liberamente sotto l’azione della gravità. La g. viene così a svolgere un ruolo in qualche modo analogo a quello delle forze apparenti nella teoria classica, in quanto è eliminabile (localmente) con una opportuna scelta del riferimento. Alla base del principio di equivalenza tra campo gravitazionale e un campo di accelerazioni vi è l’equivalenza tra massa inerziale e massa gravitazionale. Il divario tra i risultati della teoria relativistica della g. e quello della teoria classica non è comunemente molto sensibile; comunque la teoria einsteiniana è generalmente in buon accordo con i dati sperimentali e nel suo ambito, per es., si spiegano le anomalie astronomiche sopra accennate.

La g. induce sullo spazio-tempo una complessa struttura geometrica, in cui non valgono le leggi della geometria euclidea ordinaria; essa è caratterizzata da una curvatura e, a livello globale, da una topologia che può essere diversa da quella dello spazio ordinario. Secondo la teoria della relatività generale, il moto di un punto materiale in un campo gravitazionale ha natura geometrica e non dinamica: in altre parole, il moto non dipende dalla natura del corpo, ma solo dalla struttura geometrica dello spazio-tempo. Si può dire che essa, almeno quando il campo gravitazionale è debole, sia diventata uno strumento standard per affrontare svariate applicazioni, in maniera simile all’uso corrente della teoria di J.C. Maxwell per la descrizione dei fenomeni elettrici e magnetici; inoltre, con l’aumento dell’accuratezza strumentale accessibile, le correzioni relativistiche sono ormai parte integrante delle scienze spaziali. I progressi recenti in questo campo riguardano piuttosto l’astrofisica relativistica, lo studio delle proprietà straordinarie dei sistemi con campo gravitazionale intenso e la loro dinamica, il problema dell’unificazione tra relatività generale e teoria delle particelle elementari.

Campi gravitazionali intensi

Nel Sistema solare (e, a maggior ragione, in laboratorio), l’energia gravitazionale di un corpo è assai piccola (raggiunge il suo valore massimo, pari a 2 milionesimi dell’energia connessa alla massa, sulla superficie del Sole) e, quindi, le correzioni indotte dalla teoria della relatività generale alla dinamica newtoniana e all’elettromagnetismo sono di poco conto e, in ogni caso, non cambiano le caratteristiche qualitative del fenomeno. In caso contrario, per es. nei corpi celesti collassati e nelle prime fasi dell’Universo, gli sviluppi della teoria prevedono che insorgano fatti completamente nuovi. La topologia dello spazio-tempo può cambiare e si possono avere universi senza limite, ma finiti, come una superficie sferica in due dimensioni. Possono insorgere caratteristiche qualitativamente nuove nelle traiettorie delle particelle e dei fotoni; per es., orizzonti (cioè superfici chiuse attraversabili solo dall’esterno verso l’interno) e linee temporali chiuse, che comportano ‘macchine del tempo’ e violazioni della causalità. In presenza di linee temporali chiuse un corpo materiale può ritornare a un suo evento anteriore e, pertanto, non è più valido il tradizionale punto di vista di P.-S. de Laplace, secondo cui il passato determina il futuro. Sono possibili punti singolari, dove la curvatura dello spazio-tempo (e anche la densità della materia e dell’energia) è infinita.

Relatività generale e particelle elementari

Per la descrizione del mondo fisico sono usati due diversi schemi teorici: per oggetti macroscopici sono sufficienti la teoria della relatività generale e l’elettromagnetismo; per atomi e particelle elementari occorre invece la meccanica quantistica, che comporta un assetto epistemologico completamente diverso, in cui ciò che si evolve non sono campi classici come il campo gravitazionale, ma la cosiddetta funzione di stato del sistema, che descrive simultaneamente le infinite possibilità di realizzazione del sistema. L’unificazione tra questi due schemi è un compito primario della fisica teorica. Si potrebbe pensare che per i buchi neri, oggetti macroscopici, gli effetti quantistici caratteristici non abbiano alcuna rilevanza e sia sufficiente per la loro descrizione la teoria della relatività generale. Già nel 1974 S.W. Hawking ha mostrato che ciò è falso. In precedenza era stato notato che la dinamica dei buchi neri, inclusa la loro fusione, obbedisce a leggi assai simili alle leggi della termodinamica ed è possibile definire per ciascuno di essi una temperatura T, inversamente proporzionale alla massa. Per le masse tipiche dei corpi celesti essa è assai piccola: appena un decimilionesimo al di sopra dello zero assoluto per buchi neri aventi la massa del Sole (10³⁰ kg); ma per buchi neri di 10¹² kg, per es., tale temperatura raggiunge 1000 miliardi di gradi. Ora, nella meccanica quantistica il vuoto ha una complessa struttura ed è popolato da coppie di particelle e antiparticelle che però non vengono normalmente rivelate, a meno di agire sul vuoto con energie almeno uguali all’energia di riposo della coppia. Hawking ha scoperto che il buco nero è in grado di estrarre dal vuoto quantistico coppie di particelle e fotoni, e ha mostrato che esse vengono emesse con la stessa intensità e la stessa distribuzione spettrale corrispondente a un corpo ordinario con la temperatura T precedentemente introdotta. I buchi neri quindi perdono continuamente energia e massa e, alla fine, scompaiono; nel passato dell’Universo questa evaporazione ha un effetto trascurabile per masse stellari, ma può essere importante per masse più piccole (i cosiddetti minibuchi neri).

È probabile che nella teoria unificata lo spazio-tempo appaia come un fenomeno derivato e secondario e che la dinamica vera di un sistema si svolga in strutture geometriche assai più complesse, quali le stringhe, e con un numero maggiore di dimensioni. Si pensa che lo spazio-tempo stesso sarà quantizzato e anche diverse topologie saranno descritte non da un’evoluzione deterministica, ma da una funzione di stato che ne rappresenta simultaneamente la varietà e dà un peso preciso a ciascuno dei suoi modi di manifestarsi. La strada da percorrere per ottenere questa teoria unificata resta, in ogni caso, tutt’altro che chiara.

Onde gravitazionali

Un’onda gravitazionale è un campo gravitazionale trasversale e quadrupolare, che si propaga nello spazio, anche vuoto, con velocità c pari a quella della luce. L’aggettivo ‘trasversale’ si riferisce al fatto che tale campo determina sui corpi materiali che incontra sul suo cammino una distribuzione di sforzi che hanno direzione giacente nel piano (x₂, x₃) perpendicolare alla direzione di propagazione (x₁). L’aggettivo ‘quadrupolare’ indica il carattere tensoriale di tale distribuzione degli sforzi, che è rappresentata in ogni punto da un tensore (➔) simmetrico di rango 2 nelle coordinate trasversali x₂, x₃, di modo che la posizione del baricentro del corpo materiale soggetto a tali sforzi resta invariata. L’esistenza delle onde gravitazionali è prevista dalla teoria della relatività generale di Einstein.

Le onde gravitazionali, a differenza di quelle elettromagnetiche, interagiscono molto debolmente con la materia e quindi la loro rivelazione è straordinariamente difficoltosa. Al tempo stesso, potendo attraversare indisturbate grandi strati di materia, possono offrire informazioni importanti, inaccessibili alle osservazioni elettromagnetiche, sulle sorgenti che le hanno generate. La rivelazione di onde gravitazionali aprirebbe una nuova e rivoluzionaria finestra astronomica e a tale scopo sono dedicati progetti e grandiose realizzazioni in tutto il mondo.

La più significativa conferma indiretta dell’esistenza delle onde gravitazionali è tuttora la misurazione, eseguita per la prima volta da J.H. Taylor e R.A. Hulse nel 1974, della lentissima diminuzione del periodo orbitale delle pulsar (➔) binarie, che fornisce risultati in perfetto accordo quantitativo con le perdite previste per irraggiamento di onde gravitazionali da parte di tali sistemi. La potenza emessa sotto forma di onde gravitazionali da una massa che oscilla in modo armonico è proporzionale alla massa al quadrato, all’ampiezza dell’oscillazione alla quarta potenza e alla frequenza alla sesta, la costante di proporzionalità essendo pari al rapporto tra la costante di gravitazione universale e la quinta potenza della velocità della luce nel vuoto (cioè, in unità del SI, a circa 3∙10⁻⁵²). Un’onda gravitazionale può essere rivelata misurando le piccolissime deformazioni indotte in un sistema materiale posto in un laboratorio terrestre o nello spazio. Negli esperimenti terrestri, come l’italo-francese Virgo (operativo a Cascina, Pisa), la misurazione viene effettuata mediante un sofisticatissimo sistema interferometrico, per distanze tra le masse che vanno da mezzo a qualche chilometro; esse sono sensibili su bande che vanno da 10 Hz a qualche kHz.

Lenti gravitazionali

fig.

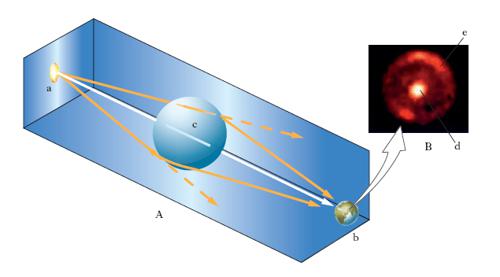
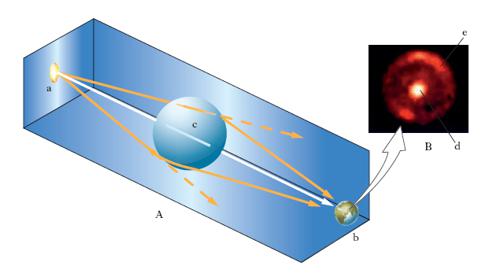
La relatività generale prevede la deflessione di un fascio di onde elettromagnetiche da parte di un corpo massivo, effetto che è stato verificato con grande precisione misurando sulla Terra la deflessione a opera del Sole della luce inviata da una stella. Benché la deflessione sia assai piccola per corpi celesti ordinari, il suo effetto sull’immagine di una sorgente viene fortemente accentuato a grandi distanze, purché sorgente, corpo deflettente e osservatore siano quasi allineati. Quando la separazione angolare tra una sorgente circolare e il corpo massivo deflettente scende al di sotto di un certo valore (proporzionale alla radice quadrata della massa), l’immagine della sorgente viene deformata in forma di arco e amplificata, mentre un’altra immagine della sorgente appare dalla parte opposta rispetto al corpo. Quando l’allineamento è perfetto, le due immagini si fondono a formare un anello concentrico con il corpo (anello di Einstein; v. fig.).