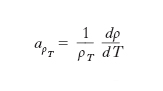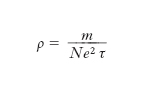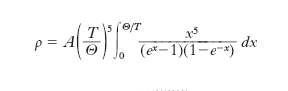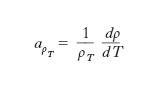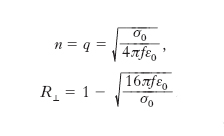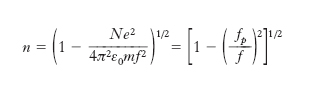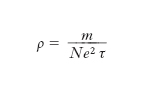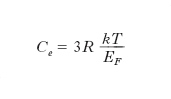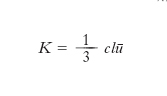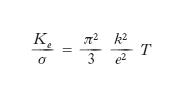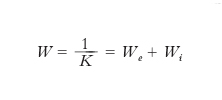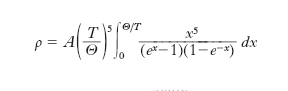metallo

Elemento chimico caratterizzato da alto potere riflettente, opacità alla luce, buona conduttività termica ed elettrica (quest’ultima decrescente al crescere della temperatura), duttilità spesso elevata, e che è inoltre capace di fornire in soluzione ioni dotati di carica positiva e di formare ossidi a carattere basico.

Chimica

Generalità

A temperatura ambiente, con l’eccezione del mercurio, i m. sono solidi cristallini; la loro struttura elettronica è caratterizzata dal fatto che gli orbitali di valenza contengono complessivamente un numero di elettroni piccolo rispetto a quello corrispondente alla loro saturazione. In relazione alla loro densità, si parla di m. pesanti, a densità relativa elevata (superiore a 4), come ferro, piombo, rame ecc., e m. leggeri, con bassa densità relativa (inferiore a 4). I m. che presentano difficoltà a ossidarsi e che, per tale motivo, possono essere rinvenuti in natura anche allo stato nativo sono detti nobili (platino, oro ecc.). Con riferimento a particolari applicazioni tecniche sono detti m. di alligazione (o di aggiunta) quelli che, aggiunti al m. base, ne modificano sostanzialmente le caratteristiche costituendo una lega metallica; m. d’apporto quelli impiegati nella saldatura. La denominazione m. bianco indica un gruppo di leghe antifrizione a base di stagno, piombo e antimonio. M. duro è la denominazione di un gruppo di leghe di elevatissima durezza, per lo più ottenute per sinterizzazione, e contenenti carburi di tungsteno, molibdeno ecc.

Metalli e non metalli

La definizione classica dei m. (in parte almeno dovuta a J.J. Berzelius) dovrebbe qualificare i m. in contrapposizione ai non metalli (questi presenterebbero caratteristiche antitetiche). In realtà non è possibile operare una distinzione netta tra le due classi di elementi in quanto, sebbene si tracci, nel sistema periodico degli elementi, una linea che permette una divisione tra le due suddette categorie, gli elementi che vengono a trovarsi vicini alla linea di separazione presentano proprietà che non possono, in maniera definita, essere qualificate né come metalliche né come non metalliche (si tratta di quegli elementi che oggi sono detti semimetalli): in altri termini, il passaggio dai m. ai non metalli, e quindi il relativo cambiamento di proprietà, avviene in modo graduale, senza apprezzabile discontinuità; ciò accade, per es., per il carattere degli ossidi la cui basicità diminuisce gradualmente nell’ambito di un periodo, da sinistra verso destra, cosicché si passa dagli ossidi basici (tipici degli elementi metallici) a quelli anfoteri e, infine, a quelli a carattere acido (tipici dei non metalli).

Conduttività elettrica

Se si volesse tentare una più esatta definizione dei m., da un punto di vista sia fisico sia chimico, si potrebbe affermare che probabilmente la caratteristica fisica che in maniera più spiccata differenzia i m. è la loro conduttività elettrica e che la misura delle proprietà chimiche di un m. è data dal suo potenziale normale nella serie dei potenziali elettrochimici. Esiste, almeno qualitativamente, una concordanza tra i due criteri di classificazione, nel senso che gli elementi che danno ioni positivi sono anche buoni conduttori elettrici. Quest’ultima proprietà è connessa alla caratteristica struttura dei m., riducibile in sostanza a un reticolo cristallino composto da atomi legati tra loro nel quale si muovono elettroni ‘liberi’ (elettroni di conduzione). Nei m., infatti, generalmente almeno un elettrone per atomo è libero di muoversi all’interno del reticolo formato da ioni positivi.

Legame metallico

In alcuni m., come i m. alcalini, l’interazione degli ioni con gli elettroni di conduzione determina il legame e quindi la coesione (legame metallico, con energie di coesione di 1-2 eV/atomo). Nei m. di transizione (i cui orbitali d sono incompleti) vi sono ulteriori sostanziali effetti di legame (con energie di coesione complessivamente di 4-9 eV/atomo) dovuti alle interazioni tra orbitali atomici interni. In termini di energia, il legame metallico, dovuto alla delocalizzazione di elettroni, è attribuibile al fatto che un livello energetico dell’atomo libero dà luogo nel m. alla formazione di una banda energetica comprendente energie maggiori e minori di quella del livello originario e che preferenzialmente si ha l’occupazione degli stati con energia minore. La sovrapposizione di orbitali d riduce ulteriormente l’energia degli stati occupati; questo fenomeno è molto rilevante nei m. di transizione a causa della sovrapposizione di orbitali incompleti (meccanismo di van der Waals-London). Sulla base del modello a elettroni liberi può spiegarsi qualitativamente il comportamento dei m., il cui studio quantitativo richiede la soluzione dell’equazione di Schrödinger per gli elettroni di conduzione sui quali agisce il campo elettrico degli ioni del reticolo cristallino.

Gli elementi metallici, a parte poche eccezioni, cristallizzano secondo strutture semplici, quali quella cubica a corpo centrato (bario, potassio, sodio, molibdeno), cubica a facce centrate (argento, ferro, rame) ed esagonale compatta (calcio, magnesio, zinco, cadmio). La teoria del legame metallico, svolta fondamentalmente da L. Pauling, permette anche di spiegare l’elevata conduttività termica e il buon potere riflettente in base al comportamento degli elettroni anzidetti. La speciale natura del legame metallico consente inoltre di giustificare il meccanismo di formazione delle leghe, cioè di quei prodotti che si originano dall’unione di due o più m. diversi.

Proprietà

Da un punto di vista più strettamente chimico i m. presentano le seguenti proprietà.

a) Formano con l’ossigeno prodotti di combinazione che vanno sotto il nome di ossidi; questi, a loro volta, con l’acqua danno origine agli idrossidi, di carattere basico, a differenza dei non m. i cui ossidi, per reazione con acqua, danno gli acidi. Quasi tutti i m. sono caratterizzati da un valore negativo della variazione di energia libera nella reazione metallo → ossido; ciò significa che la reazione di un m. nel relativo ossido è spontanea (➔ corrosione). La variazione negativa dell’energia libera è del resto caratteristica di gran parte delle trasformazioni chimiche in cui il m. passa da zero a un valore positivo del numero di ossidazione e perciò si comprende anche come i processi estrattivi dei metalli dai loro minerali, che li contengono in forma ossidata rispetto allo stato elementare, richiedano, per compiersi, energia fornita dall’esterno (sotto forma di calore, energia elettrica ecc.).

b) Esistono in soluzione come ioni dotati di carica positiva e sono capaci quindi di migrare al polo negativo, o catodo, in una cella di elettrolisi sotto l’azione di una conveniente forza elettromotrice applicata.

c) Sono capaci, uniti agli alogeni, di formare composti (alogenuri) che in genere non subiscono idrolisi in presenza di acqua. Molti m. (ma non quelli nobili) hanno un potenziale elettrochimico di riduzione maggiore di quello dell’idrogeno e sono perciò in grado di spostare quest’ultimo dagli acidi per formare i relativi sali.

Arte

L’uso dei m., dalla produzione di oggetti di arte applicata alla creazione di opere aventi valore espressivo autonomo, è diffuso fin dalle civiltà più antiche. Le tecniche di lavorazione sono elaborate in un lento processo, che dalla più semplice lavorazione a freddo di lamine di m. giunge alle tecniche di fusione, di notevole complessità esecutiva, maggiormente impiegate, per la loro potenzialità di espressione artistica, nella realizzazione di opere di scultura. Il m. più importante usato nella produzione artistica e nella scultura in m. è il rame, sia per le sue caratteristiche intrinseche di malleabilità e di resistenza agli agenti atmosferici, sia per la particolare qualità delle sue leghe come l’ottone e, soprattutto, il bronzo, materiale principalmente usato nella fusione di sculture. Nella produzione di oggetti d’uso è importante l’uso del peltro, in genere a fusione; dell’ottone (arte islamica e dell’Europa centro-settentrionale); notevole, soprattutto nella lavorazione a freddo, l’uso dell’argento, per la creazione di oggetti d’arte applicata, ornamenti, suppellettile di uso liturgico e domestico.

La lavorazione diretta, a freddo, dei m. può essere condotta per martellamento o per sbalzo della lamina metallica. Lo sbalzo è eseguito battendo con un piccolo martello sul rovescio di lamine di m., come il bronzo, o di m. prezioso per ottenere figurazioni a rilievo. La tecnica del martellamento si realizza invece martellando la superficie esterna su un modello di materiale duro, in modo che la lamina vi si adatti. La lavorazione diretta è quella prevalentemente adottata in Asia anteriore, in Egitto, in Grecia e in Etruria prima del 5° sec. a.C., per la realizzazione di sculture in m. anche di grandi dimensioni. Per comporre una scultura di grandi dimensioni è necessario utilizzare molte lamine, montate insieme su un’anima, in genere di legno, rivestita di bitume. In tale procedimento può essere necessario l’uso della tecnica della ‘ricottura’, per restituire al m. indurito dalla battitura la primitiva elasticità, e proseguirne la lavorazione. Il m. così lavorato può essere rinettato e rifinito a cesello e a bulino, oltre che con punzoni, lime e raschiatoi. Lo sbalzo e il cesello, accanto a filigrana, incisione, niello, agemina ecc. sono applicati soprattutto nella toreutica e nell’oreficeria.

La fusione e il getto diretto del m. entro forme o stampi (fusione piena) rimane a lungo limitato alla produzione di oggetti di piccole dimensioni; soltanto dalla fine del 6° sec. a.C., in Grecia, la fusione è utilizzata sistematicamente per la produzione di sculture in m. di grandi dimensioni, grazie al perfezionamento della tecnica di fusione a cera persa. L’oggetto viene modellato in cera attorno a un’anima in terra refrattaria e, a modellazione compiuta, viene rivestito con una forma esterna di terra refrattaria; esposto il tutto al calore del forno, la cera, liquefatta, esce dall’involucro di terra attraverso un piccolo foro praticato nell’involucro stesso, perdendosi; nell’incavo così ricavato, che costituisce la forma esatta dell’oggetto, viene colato il metallo che poi, una volta raffreddato e liberato dalla forma di terra, rappresenterà l’oggetto compiuto, che potrà poi a sua volta essere rifinito a freddo con lime, ceselli ecc. Anche l’anima interna viene rimossa, lasciando la scultura cava. L’oggetto finito può essere variamente patinato o dorato, e talora intarsiato con materiali diversi per la definizione ornamentale o naturalistica di particolari. L’elaborazione di tale tecnica ha una forte connessione con le potenzialità espressive e dunque anche con le innovazioni stilistiche raggiunte dalla scultura in m. che, per la notevole coesione ed elasticità del materiale, permette una notevole libertà nell’impostazione spaziale dell’opera.

La tecnica viene elaborata nel tempo, perfezionando il sistema di canali e di sfiati per l’uniforme diffusione del m. fuso e rendendo sempre più sottile lo spessore raggiunto; la riproduzione del modello con controforme in negativo, a tasselli, elaborata in età ellenistica, consente il recupero del modello originale e la sua riproduzione in serie. Secondo tale metodo, che capovolge il procedimento tradizionale, il modello è eseguito interamente in argilla; la controforma da esso ottenuta viene spalmata con uno strato di cera e la cavità restante è riempita di terra, che costituisce l’anima della matrice. Nel declino delle attività metallurgiche dopo la fine dell’epoca classica tale tecnica cade in disuso; l’industria della fusione del m., di nuovo fiorente soprattutto nel periodo romanico e gotico in Germania, Paesi Bassi e Inghilterra, non produce che raramente sculture di grandi dimensioni durante tutto il Medioevo, per ritrovare una netta evoluzione qualitativa con il Rinascimento, e una sistematica ripresa tecnica del metodo classico soltanto dalla fine del 16° secolo.

Alla prima metà del 19° sec. risale invece la scoperta del metodo galvanoplastico, che consiste nel far depositare sulla superficie interna di una forma un m. per via elettrolitica; tale procedimento resta però limitato a una produzione economica di tipo industriale, mentre nello stesso periodo la lavorazione artistica del m. rimane legata alle tecniche tradizionali.

Fisica

Le proprietà fisiche dei m., di grande interesse sia teorico sia pratico, discendono essenzialmente dalle peculiari proprietà del legame metallico e più particolarmente dall’esistenza in essi di elettroni liberi.

Proprietà elettriche

I m. sono buoni conduttori dell’elettricità. Se mantenuti a temperatura costante, essi sono conduttori ohmici, o lineari, cioè caratterizzati da una resistività elettrica ρ costante al variare dell’intensità della corrente. La resistività aumenta all’aumentare della temperatura; in un campo di temperature piuttosto ampio intorno alla temperatura ambiente, la dipendenza della resistività dalla temperatura è lineare, cioè il coefficiente termico di resistività, definito dalla relazione

(dove ρ_T è la resistività alla generica temperatura termodinamica T), è costante (per i valori delle resistività di alcuni m. puri e dei relativi coefficienti termici ➔ resistività). A bassa temperatura, tuttavia, la resistività ρ è proporzionale a T⁵ e tende a zero al tendere di T a zero. Per alcuni m., a temperature molto basse si ha un comportamento diverso, per cui anche a temperature maggiori di 0 K la resistività è praticamente nulla: è questo il fenomeno della superconduzione.

Teorie della conducibilità elettrica dei metalli

Una prima teoria della conducibilità elettrica (e termica) nei m. fu sviluppata da P. Drude nel 1900 e H.A. Lorentz nel 1902, ed è basata sul concetto di ‘gas di elettroni liberi’. Si suppone cioè che elettroni di valenza siano staccati dai loro atomi e possano essere considerati liberi di muoversi in tutto il volume del metallo. L’interpretazione più esauriente dei fenomeni di conduzione nei m. oggi disponibile è però quella offerta da una teoria quantistica, la cosiddetta teoria delle bande di livelli energetici.

Ci limiteremo qui a ricordare il risultato di una semplice trattazione semiclassica del problema, nella quale gli elettroni di conduzione sono soggetti nel m. a forze di attrito che schematizzano i meccanismi microscopici di interazione e l’effetto del potenziale atomico periodico è ricondotto all’attribuzione agli elettroni di una massa efficace (il cui valore può essere compreso tra 0,01 e 10 volte la massa dell’elettrone). Tale trattazione fornisce per la resistività la seguente espressione:

dove N è il numero degli elettroni di conduzione per unità di volume, e la carica elettronica, m la massa efficace dell’elettrone, τ il tempo medio di interazione degli elettroni nel m. (pari alla probabilità di interazione nell’unità di tempo). Nel linguaggio della teoria ‘classica’ τ corrisponde al tempo mediamente intercorrente tra due urti successivi nella serie di urti che gli elettroni incessantemente subiscono con gli ioni positivi del reticolo. Il tempo τ deve essere calcolato con i metodi della meccanica quantistica; come è evidente dalla relazione precedente, l’andamento di ρ con la temperatura è essenzialmente legato all’andamento di τ con la temperatura. Sono state elaborate varie teorie per il calcolo di τ, e quindi di ρ, nel caso di un m. ideale (cioè non contenente difetti o impurità), sotto opportune ipotesi semplificative e con vari modelli della diffusione incoerente degli elettroni da parte degli ioni del reticolo in vibrazione termica (F. Bloch, V. Weisskopf, J. Bardeen, e altri).

La relazione seguente (legge di Grüneisen-Bloch) ben si accorda con i risultati sperimentali

fig. 1

dove A è una costante per un dato m., T è la temperatura termodinamica e Θ è la temperatura di Debye per il m. in esame. Si osservi che per T≫Θ è, con buona approssimazione, ρ=AT/4Θ, cioè si trova che per temperature termodinamiche relativamente alte, ρ varia linearmente con T (andamento associato all’interazione quasi elastica tra elettroni e vibrazioni reticolari); per T≪Θ, si trova che ρ è proporzionale a T⁵ (andamento associato all’interazione fortemente anelastica). Se si riporta la grandezza ρ(T)/ρ(Θ) in funzione di T/Θ si ottiene un diagramma che rappresenta bene i risultati per tutti i m. puri (fig. 1) per temperature maggiori delle temperature critiche di superconduzione.

Proprietà meccaniche

Dal punto di vista del loro uso ha particolare importanza la proprietà, comune a gran parte dei m., di poter subire deformazioni plastiche, ossia di poter subire un cambiamento di forma per azione di forze opportunamente applicate. Tali deformazioni possono in alcuni casi essere realizzate a freddo, più spesso tuttavia si opera a caldo, entro intervalli di temperatura, variabili da m. a m., in cui risulta opportuno eseguire la lavorazione meccanica. La lavorazione a freddo, che comporta un aumento dell’energia interna del m., ha come conseguenza un miglioramento di alcune proprietà meccaniche a spese di altre (così, per es., aumenta la resistenza a trazione e diminuisce la duttilità). Un m. che abbia subito una deformazione plastica a freddo può essere riportato nelle condizioni originarie attraverso un opportuno riscaldamento a temperatura conveniente, superiore a quella di ricristallizzazione propria del m. in esame. Molti dei fenomeni che caratterizzano le proprietà meccaniche dei m. trovano spiegazione nella teoria delle dislocazioni: cioè in un genere di difetti del reticolo cristallino, preesistenti anche in m. non deformati (➔ difetto). Per quanto riguarda le proprietà meccaniche, nonostante la struttura cristallina, i m. si comportano come corpi isotropi; tale isotropia è di tipo statistico. Le proprietà meccaniche dei m. si determinano a mezzo di apposite prove (per es., prove di trazione ➔ prova).

Proprietà ottiche

Anche l’elevato potere riflettente alla luce, che conferisce ai m. la loro caratteristica lucentezza e colorazione, è una proprietà essenzialmente legata al comportamento degli elettroni di conduzione. È possibile studiare teoricamente le proprietà ottiche di un m. a partire dallo stato di libertà degli elettroni di conduzione nel m. e dalle equazioni di Maxwell dell’elettromagnetismo; i risultati che si ottengono sono in buon accordo con l’esperienza, anche fuori dal visibile, almeno fino a lunghezze d’onda non troppo corte ove cominciano a farsi sentire effetti quantistici. Per radiazioni elettromagnetiche di lunghezza d’onda λ relativamente grande, cioè per λ≫cτ (essendo c la velocità della luce nel vuoto e τ il tempo medio di interazione degli elettroni nel m.) o per 1/f≫τ (essendo f la frequenza della radiazione incidente), in pratica per λ>10 μm, si ricavano per l’indice di rifrazione assoluto n, per il coefficiente di assorbimento κ e per il coefficiente di riflessione per incidenza normale nel vuoto R_⊥ del m. espressioni che ben si accordano con i dati sperimentali:

,

dove σ₀ è la conduttività elettrica del m. per campi statici, ε₀ la costante dielettrica assoluta del vuoto e si è indicato con q il rapporto cκ/4πf. Nel caso in cui 1/f≪τ si trova invece per l’indice di rifrazione l’espressione:

fig. 2

dove N è la densità elettronica, m la massa dell’elettrone, f_p la cosiddetta frequenza di plasma per gli elettroni liberi del m. (➔ plasma). Il comportamento del m. dipende dal valore di f_p in rapporto al valore della frequenza f dell’onda. Se f_p<f, l’indice di rifrazione è reale e minore di uno: il m. è trasparente per incidenza normale (esiste però un angolo critico di incidenza oltre il quale si ha riflessione totale alla superficie del m.). Se f_p>f, n è immaginario e si ha riflessione totale alla superficie per qualsiasi angolo di incidenza; il m. risulta quindi opaco, eccetto che in spessori molto sottili (film metallici). Da quanto detto finora risulta che la trasparenza inizia a partire dalla frequenza f_p, ovvero dalla lunghezza d’onda λ_p=c/f_p; l’accordo tra i valori osservati e calcolati di λ_p è in generale abbastanza soddisfacente. Nella cosiddetta regione di rilassamento (1/τ≪f≪f_p) si trova che il coefficiente di assorbimento proporzionale a 1/f², decresce rapidamente al crescere di f. La fig. 2 mostra schematicamente il comportamento ottico di un m. al variare della frequenza dell’onda elettromagnetica incidente.

Proprietà termiche

Calori specifici

Il calore specifico di un solido può essere definito come la derivata dell’energia interna dell’unità di massa rispetto alla temperatura, a volume costante. Per un solido cristallino che non sia un m. l’energia interna da prendere in considerazione è quella relativa alle vibrazioni degli atomi del reticolo (➔ solido); per un m. va considerata anche l’energia associata al moto degli elettroni liberi. Per quanto riguarda il contributo che al calore specifico danno gli elettroni liberi, secondo la teoria classica, che assimila l’insieme di tali elettroni a un gas perfetto, tale contributo dovrebbe essere, se ciascun atomo fornisce un elettrone di conduzione, pari a (3/2)R per mole, essendo R la costante dei gas perfetti; indicando con C_a il calore molare ‘atomico’ (per vibrazioni reticolari), pari a 3R, e con C_e il calore molare ‘elettronico’, dovrebbe dunque aversi: C=C_a+C_e=3R+3R/2=9R/2. È invece noto sperimentalmente (legge di Dulong e Petit) che il calore molare, a temperature non troppo basse, è lo stesso per tutti i solidi e pari a 3R, in grave disaccordo con quanto previsto dalla teoria classica. Utilizzando per il gas di elettroni liberi la statistica quantica di Fermi-Dirac si può mostrare che questo errato risultato è dovuto a una stima sbagliata nel numero di elettroni che possono assorbire energia termica e contribuire quindi al calore specifico. Solo gli elettroni la cui energia differisce dall’energia di Fermi, E_F, di ±kT, essendo k la costante di Boltzmann e T la temperatura termodinamica, possono in pratica variare la loro energia, cioè assorbire calore, e vi sono circa 2kT/E_F elettroni in tali condizioni. Si ha allora, con buona approssimazione:

Dal momento che a temperatura ambiente kT/E_F≅0,01 per la maggior parte dei m., segue che il contributo elettronico al calore molare è soltanto dell’ordine dell’1%. Ne deriva inoltre che il calore molare elettronico dipende linearmente dalla temperatura termodinamica. Va osservato che a temperature molto basse il calore molare atomico C_a è proporzionale a T³; in tali condizioni, il calore molare totale di un m. può allora essere scritto nella forma:

C = βT³ + γT,

dove β e γ sono due opportuni coefficienti. Mentre il calore specifico dovuto alle oscillazioni reticolari decresce proporzionalmente con il cubo della temperatura, quello dovuto agli elettroni liberi decresce proporzionalmente a T e quindi, a temperature molto basse (<10 K) il contributo degli elettroni liberi al calore specifico totale può diventare rilevante.

Conducibilità termica

I m. si distinguono dagli altri solidi per essere buoni conduttori del calore; la loro conducibilità termica, K, è dell’ordine di 10² W/mK. Secondo la legge di Wiedemann-Franz, che ha carattere sperimentale, il rapporto fra K e la conduttività elettrica σ nei m. è proporzionale alla temperatura termodinamica, secondo una costante di proporzionalità uguale per tutti i m. puri e pari a 2,45·10^–8(V/K)². In pratica, però, vi sono piccole deviazioni da questo valore. I processi di trasferimento del calore nei m. avvengono per il tramite delle vibrazioni reticolari e degli elettroni di conduzione. Poiché l’agitazione termica del reticolo può essere risolta in una sovrapposizione di vibrazioni periodiche proprie (modi di vibrazione), la cui energia è quantizzata in fononi, i trasferimenti di energia delle vibrazioni reticolari possono essere descritti come processi d’urto dei fononi con le altre particelle del cristallo. Nella teoria cinetica dei gas, si trova, con certe approssimazioni:

,

dove c è il calore specifico, ū la radice quadrata della velocità quadratica media delle particelle e l il libero cammino medio di una particella fra due collisioni successive. Questo risultato può essere applicato al calcolo della conducibilità termica per un m., tenendo conto che i due processi di trasferimento del calore danno luogo a due contributi alla conducibilità, uno, K_a, dovuto al reticolo e l’altro K_e, dovuto agli elettroni liberi:

K = K_a + K_e.

Il libero cammino medio l_f dei fononi è dell’ordine di 10 -100 Å, il che implica che essi subiscono molte collisioni: questa è la ragione del fatto che la maggior parte dei solidi, esclusi i m., sono cattivi conduttori termici. Il libero cammino medio degli elettroni di conduzione nei m., l_e, è considerevolmente maggiore, cosicché in essi la conducibilità termica è essenzialmente affidata, come la conducibilità elettrica, a tali elettroni. In questo fatto trova anche validità la legge di Wiedemann-Franz. Usando per σ=1/ρ, c_e e K_e le espressioni ricavate sopra, si ottiene:

,

relazione che è in buon accordo con la legge di Wiedemann-Franz. Se si aumenta il numero di impurità in un m. (per es. formando una lega), il libero cammino medio degli elettroni diminuisce fino a divenire paragonabile a quello dei fononi, cosicché molte leghe sono relativamente cattive conduttrici del calore.

La resistività termica W totale, cioè l’inverso di K, per un m. discretamente puro a basse temperature (all’incirca minori di un decimo della temperatura di Debye Θ) è la somma di due termini, uno W_e, dovuto al contributo elettronico, l’altro W_i, dovuto alla presenza di impurità:

W_i è connessa alla resistività elettrica residua ρ_i del m. dalla legge di Wiedemann-Franz: W_i=ρ_i/(L T); d’altra parte, si può mostrare che W_e è proporzionale a T² (per T<Θ/10); in definitiva, si può scrivere:

W = ηT² + ξ/T,

fig. 3

essendo η e ξ due opportuni coefficienti. La curva di fig. 3, che si riferisce al rame, è, al riguardo, tipica per un m. puro.

Storia

Età dei m.

Il periodo preistorico nel quale l’uomo cominciò a utilizzare tecniche metallurgiche. Tradizionalmente si divide in una fase o età eneolitica, caratterizzata dall’uso del rame; in una fase o età del Bronzo; in una fase o età del Ferro.

Tecnica

Sono considerati m. preziosi l’oro, l’argento, il platino e il palladio. La qualifica deriva da alcune caratteristiche proprie di questi metalli. La rarità, che ne determina un alto valore, anche se è essenziale, non è sufficiente. Il m., infatti, oltre che raro, deve essere inalterabile e, inoltre, deve essere facilmente maneggiabile e immagazzinabile: così, non si considerano m. preziosi i m. radioattivi, anche se hanno un grande valore intrinseco, proprio perché non sono inalterabili e richiedono particolari e costose attrezzature per il trasporto e la conservazione.

Mentre il platino e il palladio sono stati conosciuti e apprezzati nel loro valore solo dal 19° sec., l’oro e l’argento lo sono stati da sempre, sì da essere utilizzati anche come mezzo di pagamento. La loro importanza in questo senso si è andata gradualmente riducendo. Il progresso scientifico e tecnologico, d’altra parte, ha ampliato la gamma degli impieghi dei m. preziosi, non più riservati soltanto ai tradizionali settori della gioielleria, dell’arredamento, della coniazione di medaglie e monete commemorative e simili, ma utilizzati largamente anche nell’industria. L’oro, l’argento, il platino sono usati, per es., nei componenti elettronici, specie di alta precisione, e la spugna di platino è uno dei principali catalizzatori dell’industria petrolchimica.

In Italia i m. preziosi possono essere commerciati ai seguenti titoli: per l’oro, 750 millesimi, 585 millesimi, 375 millesimi; per l’argento, 925 millesimi, 800 millesimi; per il platino, 950 millesimi, 900 millesimi, 850 millesimi; per il palladio, 950 millesimi, 500 millesimi. Gli oggetti di platino, palladio, oro e argento fabbricati in Italia devono portare impresso il titolo stesso e il marchio di identificazione.