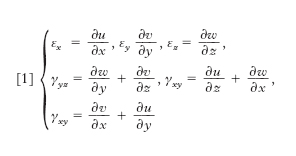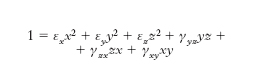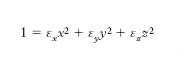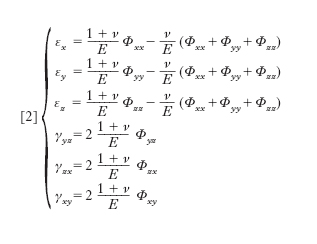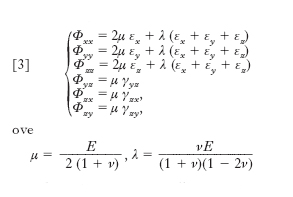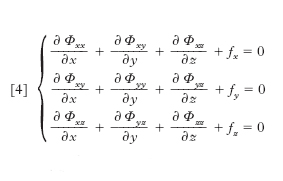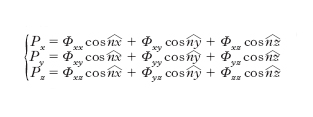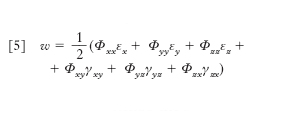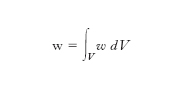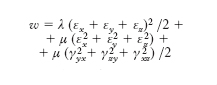elasticità

Economia

Si parla genericamente di e. nel senso di più o meno intensa reattività di un fenomeno al variare di un altro, ma con linguaggio più rigoroso si considera elastico un fenomeno soltanto quando vari in misura proporzionale o più che proporzionale al variare dell’altro. Il grado di e. si misura con il valore numerico risultante dal rapporto tra la variazione relativa (o percentuale) del fenomeno di cui si vuol conoscere l’e. (per es., domanda di un bene) e la variazione relativa (o percentuale) del fenomeno il cui mutamento ha provocato il mutare del primo (per es., prezzo). Questo rapporto, in quanto stabilito tra le variazioni percentuali dei fenomeni posti a raffronto, non risente delle unità di misura (euro, metri, litri) in cui i fenomeni siano misurati. Il rapporto, se in valore assoluto è uguale a uno o maggiore di uno, denota e., e in caso contrario anelasticità o rigidità.

Particolare rilievo ha nella scienza economica lo studio dell’e. della domanda (o richiesta) e dell’e. dell’offerta, ossia della reattività con la quale la quantità domandata e quella offerta di un bene o di un fattore di produzione si modificano al variare del prezzo. L’ e. della domanda di un bene o di un fattore di produzione rispetto al prezzo è generalmente negativa mentre l’ e. dell’offerta è positiva. Con riferimento alle rappresentazioni grafiche delle curve di domanda e offerta, si parla in particolare di e. arcuale e di e. puntuale, ossia di e. relativa a un tratto delle curve stesse e di e. relativa a un punto. Sono rare infatti le curve che presentano in tutti i loro punti la stessa e. (le domande relative si dicono a spesa costante), mentre comunemente l’e. è diversa nei vari punti e, nelle curve di domanda, massima (in valore assoluto) in corrispondenza degli alti prezzi, e decrescente con il diminuire dei prezzi stessi. Va notato inoltre che la domanda dei beni di prima necessità e quella dei beni di lusso sono in genere assai meno elastiche di quelle dei beni intermedi tra le due categorie suddette e di quelli voluttuari, mentre la richiesta dei beni surrogati (o succedanei) di quelli e suscettibili di vari usi è più elastica di quella dei beni complementari, e dei beni a una sola destinazione e insostituibili. Oltre e più che in considerazione della qualità propria del bene, l’e. della domanda varia poi in rapporto alle condizioni economico-sociali dei richiedenti e pertanto l’e. della domanda può essere riferita, oltre che alle variazioni del prezzo, anche alle variazioni del reddito dei richiedenti. L’e. della domanda rispetto al reddito assume normalmente valori positivi, salvo che per i beni inferiori la cui domanda, rispetto al reddito, ha invece una e. negativa. Si parla inoltre di e. incrociata nel caso del rapporto tra la variazione percentuale della quantità domandata di un bene e la variazione percentuale del prezzo di un altro bene. Essa può essere positiva (come per i beni succedanei), negativa (come per i beni complementari) o nulla.

Qualora ci si occupi della domanda di un fattore di produzione, invece che di un bene, ci si rende poi conto di come sull’e. della stessa influiscano la variazione della e. della domanda dei beni alla cui produzione il fattore è destinato, la misura in cui il fattore partecipa al costo totale di produzione, la facilità con cui può essere sostituito da altri fattori e le variazioni di prezzo degli altri fattori. La possibilità di variazione delle combinazioni produttive in funzione del variare del prezzo dei vari fattori di produzione è detta in particolare e. di combinazione, mentre la variabilità della quantità domandata di un fattore di produzione o di un bene finale in funzione della variazione del prezzo di altro fattore o bene sostituibile dal primo, è detta e. di sostituzione.

Di e. dell’offerta si parla più in riguardo alle possibilità di dilatazione dell’offerta stessa per aumento del prezzo, che in rapporto alla contrazione per diminuzione del prezzo ( e. negativa), dato che questa ultima è meno frequente; mentre nei periodi brevi la curva di offerta reagisce soltanto alle variazioni del prezzo, nei periodi lunghi risente poi anche delle varie possibilità di mutare il volume della produzione legate alla durata del ciclo produttivo e all’andamento dei costi. In particolare, si parla di e. dell’offerta del lavoro in funzione del variare del saggio dei salari, e. tendenzialmente nulla nei sistemi economici sviluppati, che hanno raggiunto un alto livello di industrializzazione, e tendenzialmente infinita nei sistemi economici arretrati o sottosviluppati, allo stadio prevalentemente agricolo.

Grande rilievo ha avuto nella scienza economica l’espressione e. delle aspettative, nel senso di rapporto tra la variazione percentuale dei livelli dei prezzi attesi in un determinato momento per una serie di momenti futuri e la variazione percentuale già subita dai prezzi attuali. Se la caduta o l’aumento dei prezzi previsti risultano esattamente proporzionali alla caduta o all’aumento dei prezzi attuali, le aspettative sono dette statiche; se invece il rapporto è superiore o inferiore all’unità si realizzano ipotesi dinamiche, in previsione delle future variazioni dei prezzi si avranno infatti anticipi di acquisti e ritardi di vendite o viceversa.

Con riferimento all’attività economica di un paese si parla di e. dell’economia nazionale, sia nel senso di adattabilità delle importazioni ed esportazioni del paese alle variazioni dei cambi sia in quello di reattività della produzione all’aumento della domanda legata all’esistenza di risorse non ancora sfruttate. È detta inoltre e. di un sistema economico la sua capacità di reazione al mutare delle circostanze, capacità che risente sia delle varie fasi congiunturali, sia delle crescenti rigidità tecnologiche e istituzionali dei sistemi economici moderni.

In finanza si parla di e. di un’imposta, nel senso di automatico adeguarsi del gettito del tributo all’aumentare o diminuire della materia imponibile senza bisogno di periodiche revisioni degli accertamenti: elastiche sono, pertanto, le imposte indirette, in particolare quelle sui consumi, e rigide quelle dirette.

Con riguardo al credito si parla di e. del sistema creditizio nel senso di più o meno pronta variazione della massa dei depositi bancari al variare dell’ammontare dei crediti concessi dalle banche.

Nel linguaggio tecnico è detta poi e. di cassa la conseguenza della concessione di un credito da parte della banca destinato a soddisfare le saltuarie e momentanee esigenze finanziarie del cliente e quindi caratterizzato da un succedersi, nel conto acceso al cliente beneficiario, di saldi a credito e debito del correntista per il verificarsi di frequenti prelevamenti e versamenti. E. di un conto è la frequente variazione negli sbilanci a debito e a credito del suo titolare.

Dal lato della funzione di produzione, l’ e. di sostituzione misura il rapporto tra le variazioni percentuali dei fattori produttivi (capitale e lavoro) che lasciano inalterata la produzione complessiva. In termini geometrici l’e. di sostituzione misura la pendenza dell’isoquanto di produzione.

Fisica

Proprietà dei corpi di subire, sotto l’azione di determinate sollecitazioni, deformazioni elastiche, accompagnate dal destarsi di reazioni interne, sforzi o tensioni, tendenti a far ritornare il corpo nelle condizioni primitive. La deformazione generalmente si riflette sia sulla forma sia sulle dimensioni del corpo. Talvolta però può essere interessata, almeno prevalentemente, l’una e non le altre o viceversa, e si parla allora, a seconda del caso, di una e. di forma o di volume. Un fluido, per es., presenta soltanto un’e. di volume: esso reagisce elasticamente soltanto a ogni azione tendente a diminuirne il volume, mentre adatta senza opposizione la sua forma a quella del recipiente che lo contiene. I solidi invece presentano in genere accanto a un’e. di volume un’e. di forma; talvolta, come in una sbarra cilindrica omogenea a sezione circolare assoggettata a torsione, si ha soltanto una variazione di forma.

Lo studio dei problemi inerenti all’e. dei solidi ha dato origine in matematica a importanti ricerche, nelle quali la scienza delle costruzioni trova il suo fondamento logico e le vie del suo sviluppo, sotto l’aspetto razionale. Quella che comunemente si chiama teoria matematica dell’e. si limita a considerare le piccole deformazioni dei solidi supposti perfettamente elastici. Ammettere l’ipotesi di perfetta e. equivale ad ammettere, ove la sollecitazione non sia tale da far superare alle tensioni interne un certo limite di e., che la deformazione sia proporzionale alla sollecitazione e che scompaia al cessare della causa che l’ha prodotta. A rigore nessun solido naturale si comporta così: si ha sempre una deformazione residua o permanente, e si hanno cioè sempre fenomeni di isteresi o eredità. Tuttavia in molti casi, sempre che la sollecitazione resti al disotto di certi limiti, la deformazione permanente è talmente piccola, rispetto alla pur piccola parte elastica della deformazione totale, da non essere apprezzabile dagli ordinari strumenti di misura; in questi casi l’ipotesi ideale della perfetta e. può essere accettata come abbastanza vicina alla realtà. Dalla classica teoria dell’e. restano pertanto esclusi sia i corpi anelastici, cioè i corpi che (come il piombo) subiscono deformazioni permanenti anche sotto l’azione di una modesta sollecitazione esterna, sia quelli iperelastici che (come la gomma) subiscono sotto l’azione di modeste sollecitazioni esterne deformazioni elastiche rilevantissime. Accanto a essa si sono sviluppate altre teorie matematiche (trasformazioni termoelastiche finite, plasticità ecc.), tuttora aperte alla ricerca.

Deformazioni

Le considerazioni di questo paragrafo hanno carattere puramente cinematico. In accordo con le premesse si suppone che lo spostamento s, che il generico punto P del solido subisce nella deformazione, sia molto piccolo. Così è lecito negli sviluppi in serie delle componenti u, v, w di s trascurare i termini di ordine superiore al primo, e ciò porta in definitiva a riconoscere che la deformazione in un qualsiasi intorno infinitesimo di P resta individuata dai valori che in P assumono le sei cosiddette caratteristiche o componenti di deformazione, o dello strain, cioè gli allungamenti (in senso algebrico) relativi ε_x, ε_y, ε_z che subiscono tre elementi uscenti da P, inizialmente diretti, rispettivamente, come gli assi di riferimento x, y, z e gli scorrimenti γ_yz, γ_zx, γ_xy, cioè le variazioni che subiscono gli angoli retti formati inizialmente dagli elementi medesimi, due a due. Che queste sei quantità occorrano e bastino a individuare la deformazione risulta in sostanza dal fatto che l’annullarsi identico di esse è caratteristico degli spostamenti rigidi (cui cioè non si accompagna deformazione) e che la coincidenza identica di due di tali sestuple è caratteristica di due spostamenti che differiscono soltanto per uno spostamento rigido. Le caratteristiche di deformazione risultano legate alle componenti u, v, w di s dalle relazioni

[1] formula.

Esse risultano pertanto, al pari di u, v, w, funzioni di x, y, z e sono quindi determinabili punto per punto quando siano note le tre funzioni u(x,y,z), v(x,y,z), w(x,y,z). Viceversa, date ad arbitrio sei funzioni delle coordinate, per poterle considerare come caratteristiche di una deformazione occorre che esse soddisfino a certe condizioni, dette condizioni di compatibilità o di congruenza, dovute a A.-J.-C. Barré de Saint-Venant. Le componenti di deformazione si possono interpretare come componenti di un tensore simmetrico, funzione del posto, che si chiama tensore delle deformazioni. L’andamento della deformazione nel generico punto P può essere geometricamente rappresentato mediante la quadrica o indicatrice di deformazione (introdotta da A.-L. Cauchy), con centro in P ed equazione

,

dotata delle seguenti proprietà: a) se P′ è uno dei punti d’intersezione della quadrica con un raggio uscente da P, l’allungamento unitario ε che subisce la fibra del solido inizialmente diretta come PP′ è inversamente proporzionale al quadrato della distanza di P′ da P. b) Lo spostamento del punto P′, e quindi di tutti i punti situati sul raggio vettore per P′, avviene in direzione normale alla quadrica. c) La quadrica ha tre assi; se la si riferisce a essi, la sua equazione si riduce alla forma canonica

ε_x, ε_y, ε_z si dicono allora allungamenti principali e i tre assi, assi principali di deformazione. La riduzione a forma canonica implica l’annullamento degli scorrimenti: in altri termini, in una generica deformazione, punto per punto del corpo, vi è almeno una terna di rette mutuamente ortogonali che restano tali nella deformazione. Generalmente, vi sono nell’intorno di P elementi che si allungano ed elementi che si accorciano, separati da un cono, detto cono di scorrimento o delle dilatazioni nulle, lungo le cui generatrici non si hanno né accorciamenti né allungamenti.

Tensioni

Lo stato di tensione interna conseguente alla sollecitazione cui il solido è sottoposto resta a sua volta individuato, nell’intorno di ciascun punto, da un tensore, il tensore degli sforzi, individuato da tre vettori Φ_x, Φ_y, Φ_z, rappresentanti rispettivamente gli sforzi specifici relativi a tre elementi di superficie, uscenti dal punto che si considera, mutuamente ortogonali. Componenti del tensore sono le componenti dei tre vettori rispetto alla terna delle normali x, y, z ai tre elementi di superficie. Il tensore risulta simmetrico, cioè delle nove componenti soltanto sei risultano fra loro distinte, sussistendo fra esse le cosiddette ‘proprietà di simmetria’, in virtù delle quali Φ_yz=Φ_zy; Φ_zx=Φ_xz; Φ_xy=Φ_yx. Le sei componenti distinte, cioè Φ_xx, Φ_yy, Φ_zz, Φ_xy, Φ_yz, Φ_zx, individuano lo stato di tensione nel punto, nel senso che esse bastano a individuare lo sforzo relativo a un’altra qualunque direzione; esse hanno perciò il nome di caratteristiche, o componenti di tensione o dello stress, Φ_xx, Φ_yy, Φ_zz sono tensioni normali; Φ_xy, Φ_yx, Φ_zx sono tensioni tangenziali. Anche del loro andamento nell’intorno di un punto si può dare una rappresentazione geometrica mediante la cosiddetta quadrica o indicatrice degli sforzi (➔ sforzo). Nella tecnica sono di uso corrente per le sei caratteristiche di tensione le notazioni: σ_x, σ_y, σ_z, τ_xy, τ_yz, τ_zx.

Relazioni tra deformazioni e tensioni

Ci riferiremo innanzi tutto al caso più semplice di un solido prismatico, omogeneo e isotropo sottoposto a trazione pura: in ogni punto del solido si desta soltanto uno sforzo di trazione la cui entità, costante in questo caso, a parità di forza, da punto a punto, risulta, al variare della forza, proporzionale a essa; la deformazione concomitante a tale tensione, costituita da un allungamento delle fibre parallele alla direzione della forza e da un accorciamento delle fibre a essa normali, risulta a sua volta proporzionale alla tensione. Precisamente, se la forza agisce nella direzione dell’asse x e Φ_xx è la grandezza dello sforzo, si ha un allungamento unitario delle fibre parallele a x di entità ε_x=Φ_xx/E e un accorciamento delle fibre parallele a y e a z di entità ε_y=ε_z=−νΦ_xx/E, dove E è il cosiddetto modulo di elasticità longitudinale o modulo di Young e ν è il coefficiente di Poisson o di contrazione laterale, variabili da materiale a materiale. Questo tipo di legame fra sforzi e deformazioni domina tutta la teoria. Esso discende dalle osservazioni di R. Hooke sul comportamento delle molle di acciaio per orologi, che egli stesso riassunse (1676) nell’aforisma «ut tensio sic vis» e pubblicò, secondo la moda dell’epoca, nella forma anagrammata «Ceiiinosssttuv». La legge di Hooke trovò autorevoli conferme nelle esperienze di molti fisici, specialmente in quelle di C.-A. Coulomb sul comportamento dei fili e di E. Hodgkinson e di H.-E. Tresca sull’allungamento e sulla contrazione delle sbarre metalliche. I risultati accennati delle ricerche sulla deformazione dei solidi sollecitati a trazione pura mostrano come la natura del materiale intervenga soltanto per il tramite di due parametri, E e ν. Per un solido isotropo la stessa cosa si può ripetere per il caso di una sollecitazione qualunque, salvo che alle relazioni di semplice proporzionalità tra deformazioni e sforzi vanno sostituite altre, pur sempre lineari, ma di tipo più generale. Precisamente si ha:

[2] formula.

Queste relazioni, fondamentali nella teoria dell’elasticità dei solidi isotropi, risalgono a L.-M.-H. Navier (1821) e costituiscono in sostanza una generalizzazione della legge di Hooke conseguente a un’applicazione del principio di sovrapposizione degli effetti, lecita finché ci si limita a considerare deformazioni molto piccole. Esse consentono di esprimere la deformazione nel generico punto di solido non appena sia noto lo stato di tensione in quel punto. Le [2], risolte rispetto alle caratteristiche di tensione, si presentano nella forma

[3] formula

sono le costanti di Lamé, diverse generalmente, come E e ν, da materiale a materiale.

Equazioni generali dell’equilibrio elastico

Imponendo che un parallelepipedo infinitesimo con gli spigoli paralleli agli assi coordinati, interno al solido elastico, sia in equilibrio sotto l’azione simultanea della forza esterna (di massa) e delle tensioni interne esercitate su di esso attraverso le facce di separazione, si trova che le caratteristiche di tensione devono soddisfare in ogni punto interno alle tre equazioni indefinite

[4] formula,

ove f_x, f_y, f_z, sono le componenti secondo gli assi della forza di massa agente sull’unità di volume. Alle [4] vanno aggiunte altre tre equazioni, dette equazioni al contorno o ai limiti, che, legando la forza esterna P agente sull’unità di superficie alle caratteristiche di tensione, esprimono le condizioni alle quali queste ultime devono soddisfare sulla superficie che limita il corpo. Si ottengono imponendo le condizioni di equilibrio a una porzione di solido a forma di tetraedro infinitesimo con tre facce parallele ai piani coordinati e la quarta, obliqua, appartenente alla superficie esterna del solido, e si possono scrivere nella forma

ove P_x, P_y, P_z sono le componenti, secondo gli assi, di P e per n s’intende la normale alla superficie orientata verso l’interno del solido. Si possono trasformare le equazioni, indefinite e al contorno, negli sforzi, in altre equazioni, indefinite e al contorno, negli spostamenti: equazioni che non è qui essenziale riportare. Il problema fondamentale della teoria dell’e. è quello di determinare la deformazione che un assegnato corpo elastico subisce sotto l’azione di date forze esterne. La soluzione del problema esiste ed è unica. La determinazione analitica della soluzione effettiva ha dato luogo a importanti ricerche e alla conseguente costruzione di metodi d’integrazione. Fra i problemi particolari risolti ha speciale interesse, per la fecondità delle sue applicazioni, il cosiddetto problema di Saint-Venant, al quale si possono ricondurre almeno in via di approssimazione i principali problemi relativi all’equilibrio elastico delle travi e degli archi.

Lavoro di deformazione, energia potenziale elastica

Accanto alle equazioni generali dell’equilibrio sono da ricordare alcuni altri teoremi fondamentali che, direttamente o indirettamente, si ricollegano alla nozione di lavoro di deformazione. Si chiama lavoro di deformazione il lavoro compiuto dalle forze esterne per portare il solido da uno stato di equilibrio naturale, cioè da uno stato nel quale le tensioni interne si possono considerare identicamente nulle, a una configurazione deformata di equilibrio, quando si supponga nulla la variazione di forza viva del corpo (ciò che si consegue con una lenta e graduale applicazione delle forze). Se si ammette la perfetta e. si trova che il lavoro di deformazione per una porzione di solido di volume unitario coincide con il valore che assume la funzione

[5] formula.

La coincidenza può essere fisicamente interpretata ammettendo che il lavoro fatto dalle forze esterne si trasformi in una sorta di energia interna, accumulata come energia potenziale durante la deformazione e integralmente restituita all’atto in cui venga a mancare la sollecitazione esterna; un’energia, cioè, a spese della quale è da ritenere che avvenga il ritorno del solido alle condizioni primitive allorché scompare la sollecitazione esterna. Pertanto w ha anche il nome di energia potenziale elastica unitaria (o densità dell’energia potenziale elastica). Naturalmente il lavoro di deformazione dell’intero solido, di volume V, vale

Allorché le tensioni interne compiono un lavoro a partire da uno stato deformato, questo è dato dalla corrispondente variazione di W. La variazione che W subisce nel passaggio da uno stato a un altro non dipende dagli stati intermedi, ma unicamente dagli stati estremi. Per un solido omogeneo e isotropo, w, oltre che nella forma mista prima indicata, si può esprimere in funzione soltanto delle caratteristiche di deformazione, introducendo le [3] nella [5], nella forma

Teoria dell’e. e scienza delle costruzioni

tab. 1

tab. 2

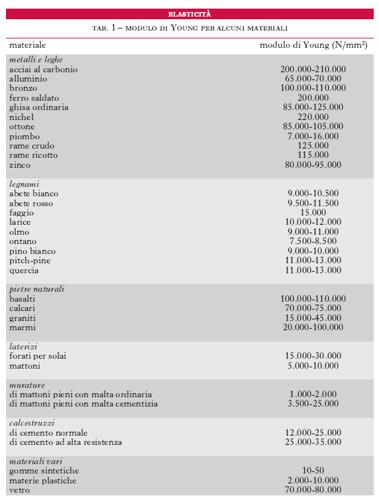
I fondamenti della teoria matematica dell’e. sommariamente riassunti nei paragrafi precedenti, trovano la loro applicazione nella scienza delle costruzioni, complesso di teorie a carattere prevalentemente sperimentale. Soltanto l’esperienza può infatti dare, attraverso opportune prove, concrete indicazioni circa le proprietà elastiche, nonché fornire i valori delle costanti elastiche dei vari materiali. Queste ultime assommano a 21 per un generico corpo anisotropo e si riducono sostanzialmente a due (per es., E e ν, oppure λ e μ) per i materiali isotropi; per questi, particolare importanza ha il modulo di Young E, del quale, in tab. 1, sono riportati i valori medi per vari materiali; in tab. 2, sono riportati i valori del coefficiente di Poisson ν per alcuni materiali.