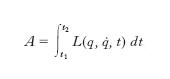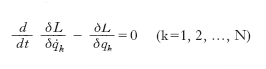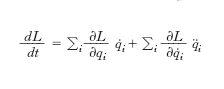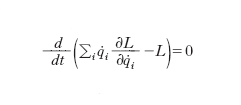conservazione

Alimentazione

Insieme delle tecniche che tendono ad arrestare o rallentare i processi vitali che si svolgono in un prodotto alimentare non trattato rendendolo non commestibile. Esse permettono quindi l’impiego differito nel tempo dell’alimento, favorendone anche il trasporto e l’uso a distanza.

Metodi di conservazione

Tutte le tecniche di c. dei cibi puntano a bloccare o a rallentare l’azione naturale dei microrganismi che si nutrono di sostanze organiche, modificandone la natura. In alcuni casi si cerca di ridurre l’effetto degli enzimi, catalizzatori naturali presenti nei cibi stessi che amplificano e favoriscono l’azione dei microrganismi. Vengono usati metodi basati su mezzi fisici e chimici.

I metodi fisici utilizzano l’azione del freddo (refrigerazione, congelamento), l’azione del calore (pastorizzazione, sterilizzazione), la disidratazione (essiccamento, liofilizzazione), l’azione di gas inerti (atmosfere controllate), l’azione delle radiazioni (raggi X e gamma).

I metodi chimici utilizzano sostanze naturali o artificiali, che in generale agiscono a livello della membrana cellulare o del citoplasma o del nucleo o dei mitocondri o dei vari processi enzimatici. Il prodotto chimico più usato per la c. è il cosiddetto sale da cucina, cioè il cloruro di sodio; esso esercita una debole azione batteriostatica, cioè inibisce o limita lo sviluppo dei germi disidratando le cellule batteriche (attraverso il meccanismo della pressione osmotica e, soprattutto, combinandosi con le proteine) e causandone spesso la plasmolisi; favorisce la riduzione di acqua libera nei prodotti trattati, oltre a conferire gusto, sapore e colore. Il sale viene prevalentemente usato sotto forma di salamoia (concentrazione in cloruro di sodio non inferiore al 25%) per la c. di olive e altri prodotti, mentre per conservare carne e pesce la salatura può anche essere fatta a secco, cospargendo il sale sulla superficie dei prodotti e rinnovandolo periodicamente. Altri prodotti chimici naturali impiegati sono l’aceto, l’olio, l’alcol etilico, lo zucchero. Il metodo di c. sott’aceto è applicato per lo più a ortaggi ma anche a carni e pesci, che, precedentemente cotti e conditi, vengono a costituire i prodotti marinati; per inibire lo sviluppo della flora batterica fermentativa e putrefattiva sono sufficienti basse concentrazioni di acido acetico. La c. sott’olio si usa per funghi, carciofi, olive, pesci ecc. La c. nell’alcol è applicata alla frutta che, dopo vari trattamenti, è immersa in bagno d’alcol e sciroppo; soltanto le ciliege non vengono cotte e il bagno è formato da solo alcol. Nel metodo di c. con lo zucchero (canditi e frutta sciroppata), il contenuto di zucchero deve essere superiore al 70%. Sostanze artificiali aggiunte agli alimenti come conservanti sono l’acido sorbico, l’acido benzoico e il nitrato di potassio.

Per la c. dei prodotti alimentari di origine animale si utilizzano anche l’affumicamento (ove coesiste una pluralità di meccanismi) o l’azione combinata della temperatura, del sale, del fumo.

Industria delle conserve alimentari

Essiccatura e salatura furono praticate fin dai tempi antichi da Greci e Romani. Nel Medioevo ebbero notevole diffusione, specie nei paesi nordici, pesce salato, carni affumicate e salumi (il primo preparato in barili anche in Italia: a Comacchio e a Ferrara); in Italia e in Francia venivano prodotte anche cotognate, cedrate ecc. Nel 15° sec., con l’importazione dello zucchero di canna, ebbe inizio l’industria dei frutti canditi. Nel 18° sec., iniziatasi la produzione dello zucchero dalle barbabietole, cominciò anche la fabbricazione delle conserve allo zucchero, mentre nel campo delle carni affumicate e delle carni salate grande notorietà acquistavano i prodotti dell’Emilia, specie quelli bolognesi.

La nascita dell’industria conserviera moderna nasce con il processo messo a punto dal pasticcere e inventore francese Nicolas Appert (1750-1841), consistente nello sterilizzare le sostanze alimentari, immergendole in acqua bollente entro recipienti ermeticamente chiusi. L’idea fu sviluppata in Gran Bretagna, con l’adozione di recipienti in lamiera di stagno. Oggi grande importanza viene riservata al confezionamento degli alimenti, spesso realizzato in atmosfera modificata (priva di ossigeno), in modo da rallentare il processo di ossidazione della carne o da influire sui tempi di maturazione dei vegetali. Altre confezioni sono realizzate in modo da ostacolare il passaggio della luce, la cui azione può modificare il sapore dei cibi.

Ecologia

Con c. si intende il mantenimento della qualità di un determinato ambiente e delle sue risorse o di un particolare equilibrio tra gli organismi che occupano una determinata area. In senso moderno la c. riguarda la gestione delle risorse della biosfera, senza danneggiare la diversità degli ecosistemi naturali e senza interferire con i processi di modificazione dei sistemi naturali. Questo approccio di c. del processo, che si contrappone alla c. dello status quo di singoli sistemi, corrisponde a una visione ecologica globale del sistema e rispetta il naturale progredire degli ecosistemi. La c. risponde a una logica economica di lungo periodo: sono ormai noti sia i costi del dissesto ambientale sia i benefici di una politica ambientale corretta. Questa infatti è in grado di produrre vantaggi per la collettività: per es., se si mantiene un bosco, si evitano frane e alluvioni, si permette la sopravvivenza di specie potenzialmente utili e si preservano per le generazioni future spazi liberi da fruire in termini sia ecologici sia economici. Nella logica del breve periodo, invece, la c. riduce o elimina i benefici economici prodotti dallo sfruttamento del sito; il problema si sposta dunque su un piano più politico, spesso condizionato dalle logiche di un’economia basata su ritorni economici immediati.

Fisica

Nella fisica in generale si parla di c. quando una data grandezza o proprietà fisica si mantiene invariata nel corso di determinate azioni, trasformazioni, reazioni. Si parla in particolare di c. di carica elettrica, energia, massa, quantità di moto, momento della quantità di moto (o momento angolare), numero barionico e numero leptonico, brevemente illustrati nel seguito.

Tipi di conservazione

C. della carica elettrica

Principio fondamentale secondo il quale la quantità di elettricità contenuta in un sistema isolato di corpi non può variare. Eventuali fenomeni interni di elettrizzazione, dando luogo a una separazione di cariche uguali e contrarie, non alterano la carica totale.

C. dell’energia

Uno dei principi fondamentali della fisica. L’energia totale (somma dell’energia meccanica, termica, elettromagnetica ecc.) di un sistema isolato non può subire variazioni, quali che siano le trasformazioni a cui il sistema viene assoggettato. Tenendo conto dell’equivalenza relativistica tra massa ed energia (E=mc²), viene a valere un più generale principio di c. dell’energia: in un sistema isolato si mantiene invariata l’energia totale pur di considerare anche l’energia equivalente alle masse presenti (c. della massa-energia).

C. della massa

Principio della fisica classica che postula l’invariabilità della massa di un dato sistema materiale durante un suo qualsiasi moto, quali che siano le azioni cui esso è soggetto. Il principio si traduce, per un continuo, nella cosiddetta equazione di continuità. Quando la velocità non è trascurabile rispetto a quella della luce nel vuoto (c=3∙108 m/s), diviene apprezzabile la variazione della massa m di un corpo con la sua velocità v secondo la legge m=m0/√‾‾‾‾‾‾1− ‾‾(v/c‾‾)‾‾2 (dove m0 è la massa del corpo in quiete); inoltre, stante ancora l’equivalenza relativistica su enunciata tra massa ed energia, la massa può essere convertita in energia e viceversa; non si ha più, pertanto, c. della massa e si ha invece la citata c. della massa-energia.

C. della quantità di moto e del momento della quantità di moto

Per un sistema materiale, soggetto a forze esterne a risultante nullo, e in particolare per un sistema isolato, ‘si conserva’, cioè non varia col tempo, la quantità di moto. Se è nullo il momento delle forze esterne, rispetto a un punto O, fisso o coincidente col baricentro, si conserva, invece, il momento della quantità di moto rispetto a O.

Leggi di conservazione

Fisica delle particelle elementari

Quando un sistema di particelle nucleari o subnucleari (nucleoni, mesoni, fotoni ecc.) subisce una trasformazione, alcune delle grandezze caratterizzanti il sistema non cambiano di valore. Si dice che queste grandezze ‘si conservano’ e principi, o leggi, di c. sono dette le proposizioni che affermano tale costanza. Di tali principi soltanto alcuni sono validi in generale, cioè per tutti i tipi di reazioni e d’interazioni; si tratta dei principi di c. fondamentali della fisica, e cioè quelli di c. della massa-energia, della quantità di moto, della carica elettrica, del numero barionico e del numero leptonico. Non sono invece principi generali, per es., quello di c. della stranezza e quello di c. della parità, che valgono per interazioni forti e per interazioni elettromagnetiche, ma non per interazioni deboli (➔ particelle elementari).

Leggi di c. e proprietà di simmetria

Un importante teorema, dovuto a E. Noether (1918) mostra che a una simmetria continua (o proprietà di invarianza) di un sistema fisico corrisponde la costanza nel tempo (conservazione) di una grandezza fisica. Per proprietà di simmetria di un sistema si intende l’invarianza della configurazione o più in generale delle funzioni che caratterizzano alcuni elementi del sistema rispetto a determinate trasformazioni. Un sistema è cioè simmetrico se possiamo operare su di esso con delle trasformazioni e dopo averle eseguite il sistema ha lo stesso ‘aspetto’ di prima. Nel caso del punto materiale, per es., la legge d’inerzia, che è la legge di c. della velocità del punto materiale libero, è una conseguenza delle proprietà di simmetria dello spazio e del tempo.

Le leggi di c. possono essere ottenute in modo elegante e relativamente semplice utilizzando il formalismo lagrangiano della meccanica analitica. In base a esso, un sistema meccanico è completamente caratterizzato da una funzione lagrangiana, o di Lagrange, L (q1, q2, ..., qN, q̇1, q̇2, ..., q̇N; t) delle N coordinate generalizzate q che descrivono gli N gradi di libertà del sistema, delle loro derivate rispetto al tempo q̇, del tempo t. La più generale formulazione della legge di moto del sistema è fornita dal principio di Hamilton o di minima azione: il moto tra due istanti t1 e t2 è tale che l’azione

è minima. Questo principio è traducibile nelle N equazioni di Lagrange

che determinando le funzioni q(t) costituiscono le equazioni del moto del sistema. Per descrivere il moto generalmente ci si pone in un sistema di riferimento (riferimento inerziale) rispetto al quale lo spazio è omogeneo e isotropo (rispetto al quale cioè diverse posizioni e orientazioni nello spazio di un corpo che non interagisce con altri corpi sono meccanicamente equivalenti) e il tempo è omogeneo (i diversi istanti sono equivalenti).

Punto materiale

Per l’omogeneità dello spazio e del tempo la lagrangiana di un punto materiale non interagente (libero) in moto in un riferimento inerziale deve essere invariante per traslazioni spaziali o temporali, quindi non può dipendere esplicitamente dalla posizione e dal tempo; per l’isotropia nello spazio la lagrangiana deve anche essere invariante per rotazioni, quindi non può dipendere dalla direzione della velocità e pertanto è funzione solo del modulo della velocità v, L=L(v). Dalle equazioni di Lagrange segue immediatamente che deve essere v = costante, cioè in un riferimento inerziale il moto di un punto materiale libero è rettilineo e uniforme ( legge di inerzia). Usando il principio di relatività galileiana, secondo il quale tutti i sistemi di riferimento in moto traslatorio uniforme rispetto a uno inerziale sono anch’essi inerziali e tutti meccanicamente equivalenti, si ricava che la lagrangiana di un punto materiale in moto libero rispetto a un riferimento inerziale è direttamente proporzionale al quadrato della velocità, cioè L=mv²/2, m è la massa del punto materiale e mv²/2 la sua energia cinetica.

Sistemi di punti materiali

Per l’additività delle lagrangiane di sistemi non interagenti, la lagrangiana di un sistema di n punti materiali non interagenti è data da L=Σ_i m_i v_i ²/2. Se si considera un sistema di punti materiali interagenti tra loro ma non con altri corpi (sistema isolato), si può tener conto delle interazioni sottraendo alla lagrangiana dei punti materiali non interagenti, cioè all’energia cinetica, una funzione delle coordinate, V, detta energia potenziale del sistema, la cui forma dipende dalla natura delle interazioni. Si ha pertanto L=Σ_i m_i v_i ²/2−V (r₁, r₂, … r_n) dove r_i è il raggio vettore dell’i-esimo punto materiale del sistema.

Per l’omogeneità del tempo le proprietà meccaniche di un sistema di punti nateriali isolato debbono essere invarianti per traslazioni temporali, quindi la lagrangiana del sistema non può dipendere esplicitamente dal tempo (∂L/∂t=o), si ha pertanto

e sostituendo, grazie alle equazioni di Lagrange, ∂L/∂q_i con d (∂L/∂q̇_i) /dt si ottiene

cioè la grandezza E=Σ_i q̇_i ∂L/∂ q̇_i−L, detta energia meccanica del sistema, è costan;te nel tempo (legge di c. dell’energia meccanica). La legge di c. dell’energia così trovata è valida oltre che per i sistemi isolati anche per i sistemi che sono soggetti a interazioni esterne che non dipendono dal tempo (anche in questo caso ∂L/∂t=0). Un sistema per il quale si conserva l’energia meccanica si dice conservativo. Sostituendo nell’espressione di E l’espressione di L ricavata in precedenza si ottiene E=Σ_i m_i v_i ²/2+V (r₁, r₂, ..., r_n), cioè l’energia meccanica del sistema è la somma dell’energia cinetica e dell’energia potenziale.

Una seconda legge di c. per i sistemi ha origine dalla invarianza per traslazioni spaziali. Per l’omogeneità dello spazio infatti le proprietà meccaniche di un sistema isolato non debbono variare in una qualsiasi traslazione nello spazio di tutto il sistema, cioè la lagrangiana del sistema deve essere invariante per traslazioni spaziali. Si consideri una traslazione infinitesima ε, in virtù della quale r_i → r_i + ε, la conseguente variazione della lagrangiana dL=Σ_i (∂L/∂r_i)∙ ε (dove con ∂L/∂r_i si indica un vettore le cui componenti sono uguali alle derivate di L rispetto alle omologhe componenti di r_i) deve essere nulla affinché la lagrangiana sia invariante; per l’arbitrarietà di ε ciò equivale a dire che deve essere Σ_i ∂L/∂r_i=0, quindi, facendo uso delle equazioni di Lagrange, d (Σ_i ∂L/∂v_i) /dt=0. Pertanto la grandezza Q=Σ_i ∂L/∂v_i=Σ_i m_i v_i, detta quantità di moto del sistema, è costante nel tempo (legge di c. della quantità di moto).

Analogamente, dall’invarianza per rotazioni nello spazio discende la conservazione del momento della quantità di moto dei sistemi isolati.

Campi

Considerazioni analoghe possono essere effettuate nello studio di un campo (come, per es., il campo elettromagnetico, in generale quantistico e relativistico), in questo caso facendo uso della funzione densità di lagrangiana. Si trova così, per es., che le grandezze conservate connesse con una traslazione infinitesima spazio-temporale sono le componenti del quadrivettore energia-impulso, mentre gli invarianti connessi con una rotazione nello spazio-tempo rappresentano i tensori del momento angolare orbitale e di spin del campo.