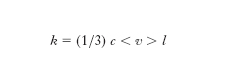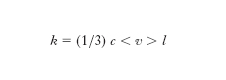conducibilità
conducibilità Proprietà dei corpi di trasmettere il calore ( c. termica) o l’elettricità ( c. elettrica) e coefficiente che misura questa proprietà. Per quest’ultimo si usa spesso, in modo del tutto equivalente, il nome di conduttività.
La c. in termologia
La c. o meglio il coefficiente di c. termica interna è il coefficiente che misura l’attitudine di una sostanza a trasmettere il calore per conduzione; da esso si distingue il coefficiente di c. termica esterna (o coefficiente di trasporto di calore), che misura l’attitudine agli scambi di calore tra la superficie di un corpo e un fluido circostante, per convezione e per irraggiamento. Nel SI il coefficiente di c. interna va espresso in W/(m•K), l’altro in W/(m2•K). Più precisamente la c. (termica interna) in un punto di un mezzo termicamente isotropo è definita come il rapporto fra il valore assoluto del flusso termico in quel punto e il gradiente della temperatura nel punto stesso (➔ conduzione). In termini finiti è la quantità di calore che si trasmette per unità di tempo e di superficie da una faccia all’altra di un corpo con facce piano-parallele, a distanza unitaria e fra cui esista una differenza di temperatura unitaria.
La c. termica è dovuta alla trasmissione di energia fra costituenti elementari contigui, senza trasporto di materia. Nei gas e nei liquidi è dovuta quindi al moto di agitazione termica delle molecole. Nei solidi cristallini, costituiti da atomi (o ioni) che vibrano attorno a posizioni fisse del reticolo cristallino e, eventualmente, da elettroni liberi (o di conduzione, responsabili della c. elettrica), il calore è condotto da fononi (i quanti dell’energia delle vibrazioni reticolari) e dagli elettroni liberi. Nei cristalli metallici, in cui è presente almeno un elettrone libero per atomo la c. è essenzialmente dovuta agli elettroni e il contributo dei fononi è trascurabile. Negli isolanti, non essendovi elettroni liberi, la c., bassa, è dovuta esclusivamente ai fononi. Due meccanismi minori di trasporto del calore nei solidi sono quello per fotoni, rilevante ad alte temperature nei cristalli trasparenti alla radiazione infrarossa, e quello per magnoni (i quanti dei moti collettivi di spin), presente in alcune sostanze magnetiche. Nei plasmi la c. è dovuta a ioni ed elettroni liberi.
Per gas ideali, la teoria cinetica fornisce per la c. termica l’espressione
[1] formula
dove c è il calore specifico volumico, 〈v> è la velocità media delle molecole, l il cammino medio percorso da una molecola fra due urti successivi. La [1] si ricava con un ragionamento in base al quale ogni molecola trasporta un’energia proporzionale a c con velocità 〈 v > a una distanza media l. Sebbene ricavata per gas ideali, la [1] risulta approssimativamente valida anche per gas reali, plasmi, liquidi e, con un’opportuna interpretazione dei simboli, per i solidi cristallini. Per i solidi cristallini isolanti l è il libero cammino medio dei fononi. Per i solidi cristallini metallici l è il libero cammino medio degli elettroni e c è il calore specifico fornito dalla statistica di Fermi-Dirac. Attorno alla temperatura ambiente la c. termica dei solidi è indipendente dalla temperatura T, mentre a temperature più basse cresce (a causa della diminuita probabilità degli urti tra fononi e tra elettroni e fononi; isolanti come il diamante divengono ottimi conduttori di calore a temperature attorno ai 100 K), per poi diminuire nuovamente a temperature che si avvicinano allo zero assoluto (proporzionalmente a T per i metalli e proporzionalmente a T3 per i cristalli isolanti). Quest’ultimo andamento si spiega considerando che anche in assenza di urti il cammino dei fononi o degli elettroni non può crescere perché limitato dalle facce del cristallo; 〈v> di fononi ed elettroni liberi è indipendente dalla temperatura e quindi k diviene proporzionale al calore specifico c, espresso dalla teoria di Debye per i cristalli isolanti e dalla statistica di Fermi-Dirac per i metalli. Valori della c. termica a temperatura ambiente per alcuni materiali sono riportati nella tabella.
La c. in elettrologia
In elettrologia, la c. elettrica, nei mezzi conduttori elettrici lineari è la grandezza rapporto tra la densità di corrente e l’intensità del campo elettrico. In generale è una grandezza tensoriale e complessa, che nel caso, frequentissimo, di mezzi lineari soggetti a campi elettrici stazionari o quasi-stazionari si riduce a una grandezza scalare, pari alla conduttanza per unità di volume o all’inverso della resistività (➔) del mezzo. L’unità di misura SI della c. elettrica è il siemens a metro (S/m).
La c. elettrica di un mezzo materiale viene attribuita o alla presenza di elettroni liberi (come nel caso dei metalli) o a quella di ioni liberi (come nel caso delle soluzioni elettrolitiche), nel primo caso si parla di conduttori elettronici o metallici, nel secondo di conduttori elettrolitici. Nei gas fortemente ionizzati (➔ plasma) la c. è dovuta a elettroni e a ioni liberi; nei semiconduttori (➔), a elettroni liberi e a lacune. La c. elettrica (e anche termica) di un conduttore elettronico è dovuta al moto in seno a esso dei cosiddetti elettroni di conduzione. Tali elettroni, in prima approssimazione, possono essere considerati come capaci di muoversi liberamente in seno al corpo conduttore, costituendo così una sorta di gas elettronico nel conduttore.
Semplici considerazioni portano per la conducibilità elettrica all’espressione σ = ne2l/mv (con m ed e massa e carica dell’elettrone, e n, l, v, rispettivamente densità, libero cammino medio e velocità media degli elettroni). Le prime teorie sviluppate per dedurre le proprietà conduttrici della materia in base allo stato dinamico di tali elettroni (teoria di P. Drude, 1900; teoria elettronica della materia di H.A. Lorentz, 1902) partivano dall’ipotesi che il gas elettronico anzidetto potesse esser trattato come un gas ordinario: quindi che l’energia da prendere in considerazione fosse soltanto quella cinetica e che per le velocità valesse la distribuzione di Maxwell-Boltzmann (in base alla quale la velocità quadratica media è proporzionale alla temperatura T). I risultati di tale teorie, soprattutto per quanto riguarda la dipendenza della c. elettrica σ da T, sono in forte contrasto con l’esperienza. Migliori risultati dettero le teorie ottenute applicando agli elettroni di conduzione la statistica quantica di Fermi-Dirac, anziché quella classica di Maxwell-Boltzmann. In pratica nella precedente espressione per la velocità media si deve impiegare il valore -2EF/m, dove EF è l’energia di Fermi, cioè l’energia dello stato energetico che ha uguale probabilità di essere libero oppure occupato (➔ statistica). La stessa teoria fornisce per il coefficiente di c. termica il valore k = π2nlk2T/(3√‾‾‾‾‾‾2mE‾‾F), proporzionale al prodotto tra la c. elettrica e la temperatura assoluta (legge di Wiedemann-Franz), in buon accordo con l’esperienza. Per la c. elettrica esistevano peraltro ancora gravi divergenze con la realtà: in particolare, sostanze con struttura cristallina simile avrebbero la stessa c., il che non è. Questo, e altri punti insoddisfacenti, sono stati rimossi dalla teoria delle bande energetiche degli elettroni. Tale teoria, oltre a distinguere nettamente fra elettroni di conduzione (liberi di muoversi nel cristallo) e di valenza (legati), tiene conto che in realtà il potenziale elettrico nel conduttore non è costante, ma variabile nello spazio con periodicità pari alla distanza media tra gli atomi del reticolo cristallino. Per gli elettroni va quindi considerata, accanto all’energia cinetica, anche un’energia potenziale elettrostatica, dipendente dalla distanza interatomica, e quindi variabile al variare della forma e delle dimensioni del reticolo (➔ banda).
La c. ionica di un conduttore elettrolitico dipende dalla sua natura, dalla temperatura, dalla sua geometria rispetto agli elettrodi di misura; anche il solvente esercita la sua influenza sui valori della c. ionica. P. Walden (1923) ha in prima approssimazione trovato che, quando si studiano le proprietà conduttrici di un composto in una serie di solventi, si mantiene costante il prodotto della viscosità del solvente per la c. limite. Fra le c. dei vari ioni nei differenti solventi, di particolare interesse sono i valori relativi agli ioni idrogeno e ossidrile in solventi che presentano legame idrogeno; tali valori sono infatti anomalmente elevati, ciò essendo stato interpretato sulla base di meccanismi di trasferimento a ponte. Per quanto riguarda la c. delle soluzioni elettrolitiche diluite in solventi non acquosi è innanzitutto da osservare che questa è controllata dall’equilibrio delle coppie ioniche, a sua volta determinato dal valore della costante dielettrica del solvente; al decrescere di questa diminuisce anche la c. con un andamento approssimativamente esponenziale. C. equivalente In una soluzione elettrolitica, il rapporto tra la c. e la concentrazione del soluto espressa in grammoequivalenti per litro di soluzione. C. specifica C. di 1 cm3 di soluzione (misurata tra due elettrodi di 1 cm2 di superficie distanti tra loro 1 cm). C. molecolare Il prodotto della c. specifica per il volume, in cm3, in cui è disciolta una grammomolecola. C. limite In un elettrolito completamente dissociato la c. pari alla somma delle c. del catione e dell’anione. Tale dissociazione completa si ha quando la concentrazione tende a zero; per questo si parla anche di c. a diluizione infinita.